面试——数据结构与算法
1、快速排序:
2、哈夫曼树:
哈夫曼树是带权路径长度最短的树。
3、最小生成树:
最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html
(1)Prim算法:不断往“点集合”中加点;
已选点集合、未选点集合;
(2)Kruskal算法:不断往“边集合”中加边;
边权值排序、检查是否在同一个连通分量(不能组成回路);
4、最短路径:
最短路径是从一点出发,到达目的地的路径最小。
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
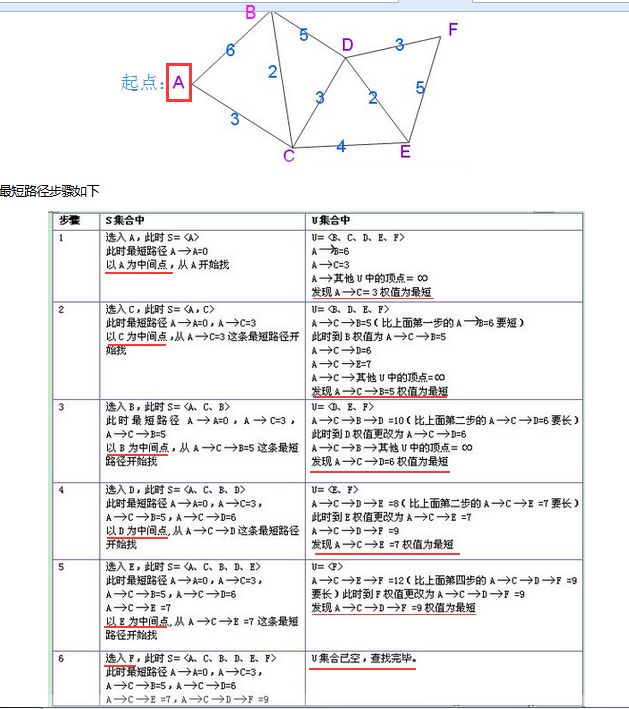
(1)Dijkstra算法
Dijkstra算法又称为单源最短路径,所谓单源是在一个有向图中,从一个顶点出发,求该顶点至所有可到达顶点的最短路径问题。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。适用于权值为非负的情况。
已求出最短路径的点集合、未求出最短路径的点集合、不断已新求出最短路径的点为中间点继续寻找,并且更新最短路径和最短距离(源点到该点的);
该算法复杂度为n^2,我们可以发现,如果边数远小于n^2,对此可以考虑用堆这种数据结构进行优化,取出最短路径的复杂度降为O(1);每次调整的复杂度降为O(elogn),e为该点的边数;所以复杂度降为O((m+n)logn)。
(2)Floyd算法
Floyd算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
a. 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b. 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
5、B树和B+树:
详见:http://blog.csdn.NET/v_JULY_v/article/details/6530142/
http://www.cnblogs.com/debuging/archive/2013/07/24/3210027.html
http://blog.csdn.Net/collonn/article/details/17923851
6、图的广度优先遍历
http://www.cnblogs.com/xwdreamer/archive/2011/06/13/2297006.html(入队列的时候访问)
http://www.cnblogs.com/sweetiemelody/p/4296524.html(弹出栈的时候访问)
8、链表的基本操作:
http://blog.csdn.net/hackbuteer1/article/details/6591486