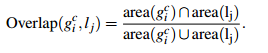Object Detection(1)

本文参考：

1）J.R.R. Uijlings “Selective Search for object recognition”

2）surgewong https://blog.csdn.net/surgewong/article/details/39316931#commentBox

3）深度学习调参实验室 https://zhuanlan.zhihu.com/p/27467369 

4）rookie_wei https://blog.csdn.net/rookie_wei/article/list/2?t=1

5)  mini猿要成长QAQ https://blog.csdn.net/sgfmby1994/article/details/78451748

------------------------------------------------------------------------------------------------------------------------------------------------------------------------ 

目标检测就是，输入一张图片，输出是将该图片中所含的所有目标物体识别，并标记出他们的位置。

分类

       假设要在图像中检测K类物体，则最终输出K+1个数，每个数代表该区域为某个类别的概率。之所以为K+1是因为还需要一个“背景类”，针对该区域无目标物体的情况。

框回归

       框回归要做的是对原始的检测框进行某种程度的“校准”，因为Selective Search获得的框有时存在一定偏差。假设Selective Search得到的框的参数为（x,y,w,h），其中(x,y)表示框左上角坐标，(w,h)表示宽和高，实际框位置为(x’,y’,w’,h’)，框回归就是要学习参数,其中，和表示和尺度无关的平移量，和表示和尺度无关的缩放量。

Selective Search for Object Recognition

       为了了解目标检测区域建议的复杂性，我们先看一组图片：

        由于我们事先不知道需要检测哪个类别，因此第一张图的桌子、瓶子、餐具都是一个个候选目标，而餐具包含在桌子这个目标内，勺子又包含在碗内。这张图（a）展示了目标检测的层级关系以及尺度关系，那我们如何去获得这些可能目标的位置呢。常规方法是通过穷举法，就是在原始图片上进行不同尺度不同大小的滑窗，获取每个可能的位置。而这样做的缺点也显而易见，就是计算量实在是太大了，而且由于不可能每个尺度都兼顾到，因此得到的目标位置也不可能那么准。那么我们能不能通过视觉特征去减少这种分类的可能性并提高精确度呢。这就是本文想做的事情。

       可用的特征有很多，到底什么特征是有用的呢？我们看第二副图片的两只猫咪，他们的纹理是一样的，因此纹理特征肯定不行了。而如果通过颜色则能很好区分。但是第三幅图变色龙可就不行了，这时候边缘特征、纹理特征又显得比较有用。而在最后一幅图中，我们很容易把车和轮胎看作是一个整体，但是其实这两者的特征差距真的很明显啊，无论是颜色还是纹理或是边缘都差的太远了。而这这是几种情况，自然图像辣么多，我们通过什么特征去区分？应该区分到什么尺度？

       Selective Search的策略是，既然是不知道尺度是怎样的，那我们就尽可能遍历所有的尺度好了，但是不同于暴力穷举，我们可以先得到小尺度的区域，然后一次次合并得到大的尺寸就好了，这样也符合人类的视觉认知。既然特征很多，那就把我们知道的特征都用上，但是同时也要照顾下计算复杂度，不然和穷举法也没啥区别了。最后还要做的是能够对每个区域进行排序，这样你想要多少个候选我就产生多少个，不然总是产生那么多你也用不完不是吗？好了这就是整篇文章的思路了，那我们一点点去看。

区域合并算法

       区域的合并方式是有层次的（hierarchical），类似于哈夫曼树的构造过程。

输入：彩色图片（三通道）
输出：物体位置的可能结果L

          1. 使用 Efficient Graph-Based Image Segmentation的方法获取原始分割区域R={r1,r2,…,rn}
          2. 初始化相似度集合S=∅
          3. 计算两两相邻区域之间的相似度，将其添加到相似度集合S中
          4. 从相似度集合S中找出，相似度最大的两个区域 ri 和rj，将其合并成为一个区域 rt，从相似度集合中除去原先与ri和rj相邻区域之间计算的相似度，计算rt与其相邻区域（原先与ri或rj相邻的区域）的相似度，将其结果添加的到相似度集合S中。同时将新区域 rt 添加到 区域集合R中。
          5. 获取每个区域的Bounding Boxes，这个结果就是物体位置的可能结果L

多样化策略

       为了尽最大可能去分割所有情景的图片我们得保持特征的多样性啊.

颜色空间多样化

       作者采用了8中不同的颜色方式，主要是为了考虑场景以及光照条件等。

       主要使用的颜色空间有：（1）RGB，（2）灰度I，（3）Lab，（4）rgI（归一化的rg通道加上灰度），（5）HSV，（6）rgb（归一化的RGB），（7）C，（8）H（HSV的H通道）

相似度计算多样化

        1. 颜色（color）相似度
        使用L1-norm归一化获取图像每个颜色通道的25 bins的直方图，这样每个区域都可以得到一个75维的向量，区域之间颜色相似度通过下面的公式计算：

         在区域合并过程中使用需要对新的区域进行计算其直方图，计算方法：

        2. 纹理（texture）相似度
        这里的纹理采用SIFT-Like特征。具体做法是对每个颜色通道的8个不同方向计算方差σ=1的高斯微分（Gaussian Derivative），每个通道每个颜色获取10 bins的直方图（L1-norm归一化），这样就可以获取到一个240维的向量，区域之间纹理相似度计算方式和颜色相似度计算方式类似，合并之后新区域的纹理特征计算方式和颜色特征计算相同：

        3. 大小（size）相似度
        这里的大小是指区域中包含像素点的个数。使用大小的相似度计算，主要是为了尽量让小的区域先合并：

       4. 吻合（fit）相似度
       这里主要是为了衡量两个区域是否更加“吻合”，其指标是合并后的区域的Bounding Box（能够框住区域的最小矩形（没有旋转））越小，其吻合度越高。其计算方式：

       最后将上述相似度计算方式组合到一起，可以写成如下，其中：

给区域打分

       通过上述的步骤我们能够得到很多很多的区域，但是显然不是每个区域作为目标的可能性都是相同的，因此我们需要衡量这个可能性，这样就可以根据我们的需要筛选区域建议个数啦。

       这篇文章做法是，给予最先合并的图片块较大的权重，比如最后一块完整图像权重为1，倒数第二次合并的区域权重为2以此类推。但是当我们策略很多，多样性很多的时候呢，这个权重就会有太多的重合了，排序不好搞啊。文章做法是给他们乘以一个随机数，毕竟3分看运气嘛，然后对于相同的区域多次出现的也叠加下权重，毕竟多个方法都说你是目标，也是有理由的嘛。这样我就得到了所有区域的目标分数，也就可以根据自己的需要选择需要多少个区域了。

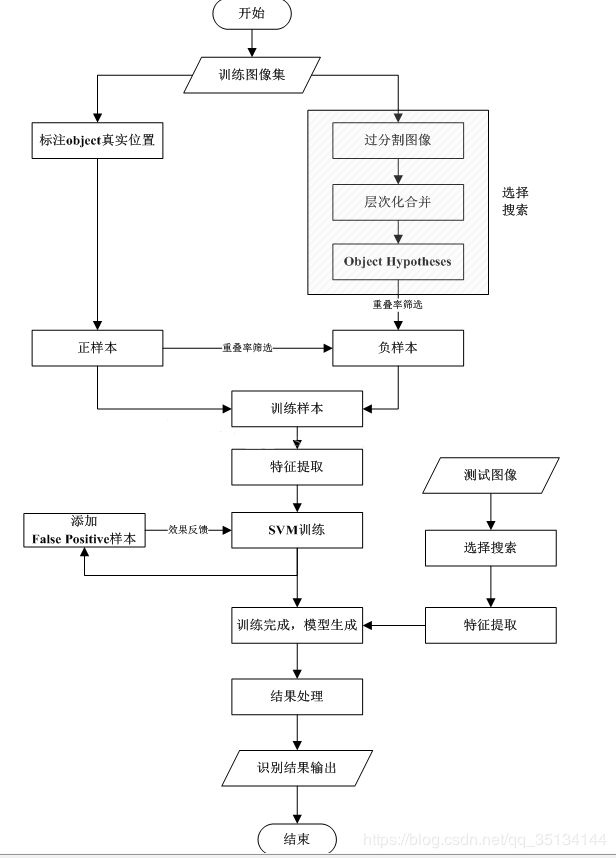
 使用选择搜索（Selective Search）进行物体识别

        通过前面的区域合并，可以得到一些列物体的位置假设L。接下来的任务就是如何从中找出物体的真正位置并确定物体的类别。 常用的物体识别特征有HOG（Histograms of oriented gradients）和 bag-of-words 两种特征。在穷举搜索（Exhaustive Search）方法中，寻找合适的位置假设需要花费大量的时间，能选择用于物体识别的特征不能太复杂，只能使用一些耗时少的特征。由于选择搜索（Selective Search）在得到物体的位置假设这一步效率较高，其可以采用诸如SIFT等运算量大，表示能力强的特征。在分类过程中，系统采用的是SVM。

 

选择性搜索性能评估

       通过算法计算得到的包含物体的Bounding Boxes与真实情况（ground truth）的窗口重叠越多，那么算法性能就越好。这是使用的指标是平均最高重叠率ABO（Average Best Overlap）。对于每个固定的类别 c，每个真实情况（ground truth）表示为 ，令计算得到的位置假设L中的每个值lj，那么 ABO的公式表达为：

重叠率的计算方式：

上面结果给出的是一个类别的ABO，对于所有类别下的性能评价，很自然就是使用所有类别的ABO的平均值MABO（Mean Average Best Overlap）来评价。

代码分析

python实现下载地址： https://github.com/AlpacaDB/selectivesearch

准备：

selectivesearch用到skimage库，

skimage库需要依赖 numpy+mkl 和scipy，

在 https://www.lfd.uci.edu/~gohlke/pythonlibs/#scikits.vectorplot  下载合适的版本。

                         

我的版本是这个，将这两个文件放在Scripts文件夹下，在命令行中该目录下 pip 安装，在此之前需安装wheel. 

安装成功后，pip 安装 scikit-image即可 

selectivesearch.py

# -*- coding: utf-8 -*-
from __future__ import division

import skimage.io
import skimage.feature
import skimage.color
import skimage.transform
import skimage.util
import skimage.segmentation
import numpy


# "Selective Search for Object Recognition" by J.R.R. Uijlings et al.
#
#  - Modified version with LBP extractor for texture vectorization


def _generate_segments(im_orig, scale, sigma, min_size):
    """
        segment smallest regions by the algorithm of Felzenswalb and
        Huttenlocher
    """

    # open the Image
    im_mask = skimage.segmentation.felzenszwalb(
        skimage.util.img_as_float(im_orig), scale=scale, sigma=sigma,
        min_size=min_size)

    # merge mask channel to the image as a 4th channel
    im_orig = numpy.append(
        im_orig, numpy.zeros(im_orig.shape[:2])[:, :, numpy.newaxis], axis=2)
    im_orig[:, :, 3] = im_mask

    return im_orig


def _sim_colour(r1, r2):
    """
        calculate the sum of histogram intersection of colour
    """
    return sum([min(a, b) for a, b in zip(r1["hist_c"], r2["hist_c"])])


def _sim_texture(r1, r2):
    """
        calculate the sum of histogram intersection of texture
    """
    return sum([min(a, b) for a, b in zip(r1["hist_t"], r2["hist_t"])])


def _sim_size(r1, r2, imsize):
    """
        calculate the size similarity over the image
    """
    return 1.0 - (r1["size"] + r2["size"]) / imsize


def _sim_fill(r1, r2, imsize):
    """
        calculate the fill similarity over the image
    """
    bbsize = (
        (max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"]))
        * (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"]))
    )
    return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize


def _calc_sim(r1, r2, imsize):
    return (_sim_colour(r1, r2) + _sim_texture(r1, r2)
            + _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize))


def _calc_colour_hist(img):
    """
        calculate colour histogram for each region

        the size of output histogram will be BINS * COLOUR_CHANNELS(3)

        number of bins is 25 as same as [uijlings_ijcv2013_draft.pdf]

        extract HSV
    """

    BINS = 25
    hist = numpy.array([])

    for colour_channel in (0, 1, 2):

        # extracting one colour channel
        c = img[:, colour_channel]

        # calculate histogram for each colour and join to the result
        hist = numpy.concatenate(
            [hist] + [numpy.histogram(c, BINS, (0.0, 255.0))[0]])

    # L1 normalize
    hist = hist / len(img)

    return hist


def _calc_texture_gradient(img):
    """
        calculate texture gradient for entire image

        The original SelectiveSearch algorithm proposed Gaussian derivative
        for 8 orientations, but we use LBP instead.

        output will be [height(*)][width(*)]
    """
    ret = numpy.zeros((img.shape[0], img.shape[1], img.shape[2]))

    for colour_channel in (0, 1, 2):
        ret[:, :, colour_channel] = skimage.feature.local_binary_pattern(
            img[:, :, colour_channel], 8, 1.0)

    return ret


def _calc_texture_hist(img):
    """
        calculate texture histogram for each region

        calculate the histogram of gradient for each colours
        the size of output histogram will be
            BINS * ORIENTATIONS * COLOUR_CHANNELS(3)
    """
    BINS = 10

    hist = numpy.array([])

    for colour_channel in (0, 1, 2):

        # mask by the colour channel
        fd = img[:, colour_channel]

        # calculate histogram for each orientation and concatenate them all
        # and join to the result
        hist = numpy.concatenate(
            [hist] + [numpy.histogram(fd, BINS, (0.0, 1.0))[0]])

    # L1 Normalize
    hist = hist / len(img)

    return hist


def _extract_regions(img):

    R = {}

    # get hsv image
    hsv = skimage.color.rgb2hsv(img[:, :, :3])

    # pass 1: count pixel positions
    for y, i in enumerate(img):

        for x, (r, g, b, l) in enumerate(i):

            # initialize a new region
            if l not in R:
                R[l] = {
                    "min_x": 0xffff, "min_y": 0xffff,
                    "max_x": 0, "max_y": 0, "labels": [l]}

            # bounding box
            if R[l]["min_x"] > x:
                R[l]["min_x"] = x
            if R[l]["min_y"] > y:
                R[l]["min_y"] = y
            if R[l]["max_x"] < x:
                R[l]["max_x"] = x
            if R[l]["max_y"] < y:
                R[l]["max_y"] = y

    # pass 2: calculate texture gradient
    tex_grad = _calc_texture_gradient(img)

    # pass 3: calculate colour histogram of each region
    for k, v in list(R.items()):

        # colour histogram
        masked_pixels = hsv[:, :, :][img[:, :, 3] == k]
        R[k]["size"] = len(masked_pixels / 4)
        R[k]["hist_c"] = _calc_colour_hist(masked_pixels)

        # texture histogram
        R[k]["hist_t"] = _calc_texture_hist(tex_grad[:, :][img[:, :, 3] == k])

    return R


def _extract_neighbours(regions):

    def intersect(a, b):
        if (a["min_x"] < b["min_x"] < a["max_x"]
                and a["min_y"] < b["min_y"] < a["max_y"]) or (
            a["min_x"] < b["max_x"] < a["max_x"]
                and a["min_y"] < b["max_y"] < a["max_y"]) or (
            a["min_x"] < b["min_x"] < a["max_x"]
                and a["min_y"] < b["max_y"] < a["max_y"]) or (
            a["min_x"] < b["max_x"] < a["max_x"]
                and a["min_y"] < b["min_y"] < a["max_y"]):
            return True
        return False

    R = list(regions.items())
    neighbours = []
    for cur, a in enumerate(R[:-1]):
        for b in R[cur + 1:]:
            if intersect(a[1], b[1]):
                neighbours.append((a, b))

    return neighbours


def _merge_regions(r1, r2):
    new_size = r1["size"] + r2["size"]
    rt = {
        "min_x": min(r1["min_x"], r2["min_x"]),
        "min_y": min(r1["min_y"], r2["min_y"]),
        "max_x": max(r1["max_x"], r2["max_x"]),
        "max_y": max(r1["max_y"], r2["max_y"]),
        "size": new_size,
        "hist_c": (
            r1["hist_c"] * r1["size"] + r2["hist_c"] * r2["size"]) / new_size,
        "hist_t": (
            r1["hist_t"] * r1["size"] + r2["hist_t"] * r2["size"]) / new_size,
        "labels": r1["labels"] + r2["labels"]
    }
    return rt


def selective_search(
        im_orig, scale=1.0, sigma=0.8, min_size=50):
    '''Selective Search

    Parameters
    ----------
        im_orig : ndarray
            Input image
        scale : int
            Free parameter. Higher means larger clusters in felzenszwalb segmentation.
        sigma : float
            Width of Gaussian kernel for felzenszwalb segmentation.
        min_size : int
            Minimum component size for felzenszwalb segmentation.
    Returns
    -------
        img : ndarray
            image with region label
            region label is stored in the 4th value of each pixel [r,g,b,(region)]
        regions : array of dict
            [
                {
                    'rect': (left, top, width, height),
                    'labels': [...],
                    'size': component_size
                },
                ...
            ]
    '''
    assert im_orig.shape[2] == 3, "3ch image is expected"

    # load image and get smallest regions
    # region label is stored in the 4th value of each pixel [r,g,b,(region)]
    img = _generate_segments(im_orig, scale, sigma, min_size)

    if img is None:
        return None, {}

    imsize = img.shape[0] * img.shape[1]
    R = _extract_regions(img)

    # extract neighbouring information
    neighbours = _extract_neighbours(R)

    # calculate initial similarities
    S = {}
    for (ai, ar), (bi, br) in neighbours:
        S[(ai, bi)] = _calc_sim(ar, br, imsize)

    # hierarchal search
    while S != {}:

        # get highest similarity
        i, j = sorted(S.items(), key=lambda i: i[1])[-1][0]

        # merge corresponding regions
        t = max(R.keys()) + 1.0
        R[t] = _merge_regions(R[i], R[j])

        # mark similarities for regions to be removed
        key_to_delete = []
        for k, v in list(S.items()):
            if (i in k) or (j in k):
                key_to_delete.append(k)

        # remove old similarities of related regions
        for k in key_to_delete:
            del S[k]

        # calculate similarity set with the new region
        for k in [a for a in key_to_delete if a != (i, j)]:
            n = k[1] if k[0] in (i, j) else k[0]
            S[(t, n)] = _calc_sim(R[t], R[n], imsize)

    regions = []
    for k, r in list(R.items()):
        regions.append({
            'rect': (
                r['min_x'], r['min_y'],
                r['max_x'] - r['min_x'], r['max_y'] - r['min_y']),
            'size': r['size'],
            'labels': r['labels']
        })

    return img, regions

example.py

# -*- coding: utf-8 -*-
from __future__ import (
    division,
    print_function,
)

import skimage.data
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import selectivesearch


def main():

    # loading astronaut image
    img = skimage.data.astronaut()

    # perform selective search
    img_lbl, regions = selectivesearch.selective_search(
        img, scale=500, sigma=0.9, min_size=10)

    candidates = set()
    for r in regions:
        # excluding same rectangle (with different segments)
        if r['rect'] in candidates:
            continue
        # excluding regions smaller than 2000 pixels
        if r['size'] < 2000:
            continue
        # distorted rects
        x, y, w, h = r['rect']
        if w / h > 1.2 or h / w > 1.2:
            continue
        candidates.add(r['rect'])

    # draw rectangles on the original image
    fig, ax = plt.subplots(ncols=1, nrows=1, figsize=(6, 6))
    ax.imshow(img)
    for x, y, w, h in candidates:
        print(x, y, w, h)
        rect = mpatches.Rectangle(
            (x, y), w, h, fill=False, edgecolor='red', linewidth=1)
        ax.add_patch(rect)

    plt.show()

if __name__ == "__main__":
    main()