(港口->目的地)最短路径算法

 今年杭电研究生数学建模的第二题——求所有出发点到目标点的最短路径路线。

• 生成最短路径：

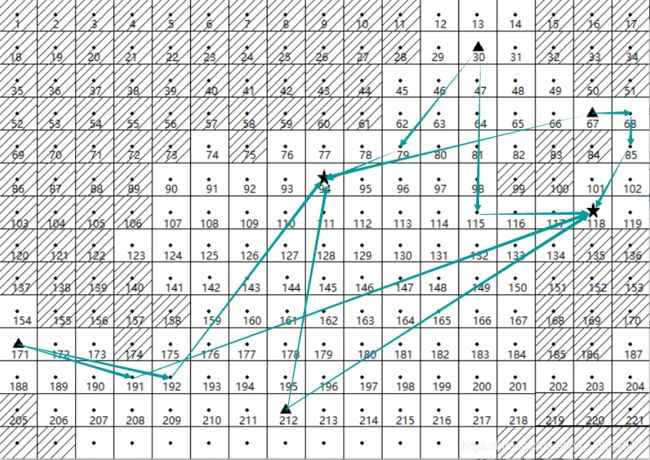
按照题目要求，首先需要生成虚拟地图，用M*N的网格地图来表示地图，网格中心点的编号来表示可通行的水域，障碍物以及潜在的被攻击目标，接下来需要生成最短路径，我们实现了两种方案：一种是用传统的Floyd求最短路径；另一种是针对题意（小船尽量走直线，如果直航道被阻挡，则选择一系列不与被阻挡方块相交的直线组成的最短路径段）实现的，我们假设小船只可能在障碍物附近改变航行方向，且最复杂的地形（即途中最多一次遇到由若干个相邻格子组成的一整片障碍物的情况）考虑最多需要改变两次方向到达目标点；两种方法生成的最短路径长度几乎相近，区别在于前者可能在距离障碍物很远的水域就改变方向，而后者只在障碍物附近调整方向，模拟现实中“绕”过障碍物的情况，如图一所示。试验多组数据后，我们综合考虑采用第二种方案来计算最短路径。

图一

方案一与方案二路径对比，最短路径的距离更短，且接近障碍物才会微调方向，较符合事实。

1.1算法描述：

①初始化地图信息：创建Point类，用于存储每个网格中心点坐标，网格编号，是否是障碍物，港口，目标以及是否被访问过的标记，用Point类创建M*N的二位数组来存储每个格子的信息；

②寻找改变航向的点：若港口到目标位置直线不可通行，则改变航向的候选点只可能出现在障碍物块周围的八个点，考虑到障碍物可能连续的情况，我们利用深度优先算法遍历得到障碍物块周围所有的改变航向的候选点，首先查找只有一个拐点就可以通行的情况，生成的新路径若不与任何障碍物有交点，则可行，路径进行存储；若找不到改变一次航向就可通行的路径，则取出候选拐点中所有点的两两组合，形成的三段路径若均可通行，则进行路径存储；

③筛选出最短路径：遍历所有存储的路径，相同港口和目标的路径，只保留最短的路径，剩下的所有路径的集合则为后续的探测器部署准备了必要条件。

1.2测试

我们测试了题目附件中所有的数据，生成路径效果均达到了预期，符合事实。生成的最短路径集合已在附件结果中给出，为测试在现实中的实用性，我们使用提供的纽约港卫星影像来检验算法的效果。如图三(1,2)所示，我们假设出如下港口，陆地全部做为障碍物来表示，实验表明，即使是较为复杂的地形，如67->68->85->118也可以搜索到最短路径，可以为后续探测器部署模型提供精确的路线图。

图三(1)纽约港卫星影像

图三(2)模拟出的地图及算法路径生成的效果

 

算法描述：

首先计算出出发点和目的地之间直连的障碍物属于哪个障碍物群，然后直接在对应的障碍物周围拐点群寻找所有可行路径，最后选出最短的那条

#include 
#include 
#include 
using namespace std;
//初始化输入参数
#define Width 17
#define Height 17
#define Size 200
#define numSize 200
const int Target[numSize] = { 94,118 };//目标ID
const int Port[numSize] = { 30,67,171,212,188,172,173,166 };//港口ID
const int Block[numSize] = { 44,61,32,50,83,84,99,100,137,138,139,140,155,156,157,158,174,151,135};//障碍物ID
//static int Target[numSize] = { 150 };//目标ID
//static int Port[numSize] = { 145 };//港口ID
//static int Block[numSize] = { 129,130,147,148,149,164,165,171,191,192 };//障碍物ID
//方法
class Point {
public:
	int x, y;//中心点坐标
	int id;
	bool isBlock = false;
	int BlockQ_num = 0;
	bool isPort = false;
	bool isTarget = false;
	bool searchFlag = false;
};
Point points[Width*Height];

Point id2Point(int id) {//找到ID号对应的点
	return points[id - 1];
}

int A, B, C;
void lineABC(int aID, int bID) {//求直线方程
	Point a = id2Point(aID);
	Point b = id2Point(bID);
	A = a.y - b.y;
	B = b.x - a.x;
	C = a.x * b.y - b.x * a.y;
}

float distance(int pID1, int pID2) {
	return sqrt((points[pID1 - 1].x - points[pID2 - 1].x)*(points[pID1 - 1].x - points[pID2 - 1].x) + (points[pID1 - 1].y - points[pID2 - 1].y)*(points[pID1 - 1].y - points[pID2 - 1].y));
}

bool isCrash(int pID, int aID, int bID) {//判断线与方块是否相交
	Point p = id2Point(pID);
	Point a = id2Point(aID);
	Point b = id2Point(bID);
	lineABC(aID, bID);//求出直线的方程参数ABC
	if (a.x < p.x - 100 && b.x < p.x - 100 || a.x > p.x + 100 && b.x > p.x + 100 || a.y p.y + 100 && b.y > p.y + 100) {
		return false;
	}
	else if (A*(p.x - 100) + B * (p.y - 100) + C > 0 && A*(p.x - 100) + B * (p.y + 100) + C > 0 && A*(p.x + 100) + B * (p.y - 100) + C > 0 && A*(p.x + 100) + B * (p.y + 100) + C > 0 || A * (p.x - 100) + B * (p.y - 100) + C < 0 && A*(p.x - 100) + B * (p.y + 100) + C < 0 && A*(p.x + 100) + B * (p.y - 100) + C < 0 && A*(p.x + 100) + B * (p.y + 100) + C < 0) {
		return false;
	}
	return true;
}

int BlockQ[100];
int BlockQ_i = 0;
int P_Guais[100];//设置障碍物周围最多候选拐点个数,存储候拐选点
int P_Guais_i = 0;

void findP_Guai(int pID) {//如果有交，求候选拐点，设a为出发点，b为目标点,输出ID号

	pID -= 1;

	//深度优先搜索拐点
	if (!points[pID].searchFlag) {
		BlockQ[BlockQ_i] = pID + 1;
		BlockQ_i++;
	}

	if (points[pID].searchFlag)
		return;
	points[pID].searchFlag = true;


	if (points[pID].x >= Size / 2 * 3 && points[pID].y >= Size / 2 * 3) {//有左上角的边界
		if (points[pID - Width - 1].isBlock && !points[pID - Width - 1].searchFlag)
			findP_Guai(points[pID - Width - 1].id);
		else if (!points[pID - Width - 1].isBlock && !points[pID - Width - 1].searchFlag) {
			points[pID - Width - 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID - Width - 1].id;
			P_Guais_i++;
		}
	}
	if (points[pID].y >= Size / 2 * 3) {//上边界
		if (points[pID - Width].isBlock && !points[pID - Width].searchFlag)
			findP_Guai(points[pID - Width].id);
		else if (!points[pID - Width].isBlock && !points[pID - Width].searchFlag) {
			points[pID - Width].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID - Width].id;
			P_Guais_i++;
		}
	}
	if (points[pID - Width].x < Size/2+Size*(Width-1) && points[pID].y >= Size / 2 * 3) {//右上边界
		if (points[pID - Width + 1].isBlock && !points[pID - Width + 1].searchFlag)
			findP_Guai(points[pID - Width + 1].id);
		else if (!points[pID - Width + 1].isBlock && !points[pID - Width + 1].searchFlag) {
			points[pID - Width + 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID - Width + 1].id;
			P_Guais_i++;
		}
	}
	if (points[pID - Width].x < Size / 2 + Size * (Width - 1)) {
		if (points[pID + 1].isBlock && !points[pID + 1].searchFlag)
			findP_Guai(points[pID + 1].id);
		else if (!points[pID + 1].isBlock && !points[pID + 1].searchFlag) {
			points[pID + 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID + 1].id;
			P_Guais_i++;
		}
	}
	if (points[pID - Width].x < Size / 2 + Size * (Width - 1) && pID + Width < Width*Height) {//右下
		if (points[pID + Width + 1].isBlock && !points[pID + Width + 1].searchFlag)
			findP_Guai(points[pID + Width + 1].id);
		else if (!points[pID + Width + 1].isBlock && !points[pID + Width + 1].searchFlag) {
			points[pID + Width + 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID + Width + 1].id;
			P_Guais_i++;
		}
	}
	if (pID + Width < Width*Height) {//下
		if (points[pID + Width].isBlock && !points[pID + Width].searchFlag)
			findP_Guai(points[pID + Width].id);
		else if (!points[pID + Width].isBlock && !points[pID + Width].searchFlag) {
			points[pID + Width].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID + Width].id;
			P_Guais_i++;
		}
	}
	if (points[pID].x >= Size / 2 * 3 && pID + Width < Width*Height) {//左下
		if (points[pID + Width - 1].isBlock && !points[pID + Width - 1].searchFlag)
			findP_Guai(points[pID + Width - 1].id);
		else if (!points[pID + Width - 1].isBlock && !points[pID + Width - 1].searchFlag) {
			points[pID + Width - 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID + Width - 1].id;
			P_Guais_i++;
		}
	}
	if (points[pID].x >= Size / 2 * 3) {
		if (points[pID - 1].isBlock && !points[pID - 1].searchFlag)
			findP_Guai(points[pID - 1].id);
		else if (!points[pID - 1].isBlock && !points[pID - 1].searchFlag) {
			points[pID - 1].searchFlag = true;
			P_Guais[P_Guais_i] = points[pID - 1].id;
			P_Guais_i++;
		}
	}
	
}
int main() {
	int index = 0;//格子ID号

	for (int i = 1; i <= Width; i++) {//初始化地图
		for (int j = 1; j <= Height; j++) {
			points[index].x = Size / 2 + (j - 1) * Size;
			points[index].y = Size / 2 + (i - 1) * Size;
			points[index].id = index + 1;//ID从1开始

			for (int i = 0; i < numSize&&Target[i]; i++) {
				if (points[index].id == Target[i])
					points[index].isTarget = true;
			}
			for (int i = 0; (i < numSize)&&Block[i]; i++) {
				if (points[index].id == Block[i]) {
					points[index].isBlock = true;
				}
			}
			for (int i = 0; i < numSize&&Port[i]; i++) {
				if (points[index].id == Port[i])
					points[index].isPort = true;
			}
			//cout << "id=" << points[index].id << "  x=" << points[index].x << "  y=" << points[index].y <<" 港口"<< points[index]. isPort<< " 目标" << points[index].isTarget << " 障碍物" << points[index].isBlock << endl;
			index++;
		}
	}
	int Q_num = 0;
	int P_GuaisQ[1000][100] = {0};
	for (int i = 0; i < numSize && Block[i]; i++) {//设置障碍物群编号及障碍物周围拐点群
		if (!points[Block[i]-1].searchFlag) {
			
			BlockQ_i = 0;
			BlockQ[100] = { 0 };
			memset(BlockQ, 0, sizeof(BlockQ));

			P_Guais[100] = { 0 };
			memset(P_Guais, 0, sizeof(P_Guais));

			for (int kk = 0; kk < Width*Height; kk++) {
				if(!points[kk].isBlock)
					points[kk].searchFlag = false;//非障碍物的地方访问标志重置
			}
			findP_Guai(Block[i]);
			/**************************************************************/
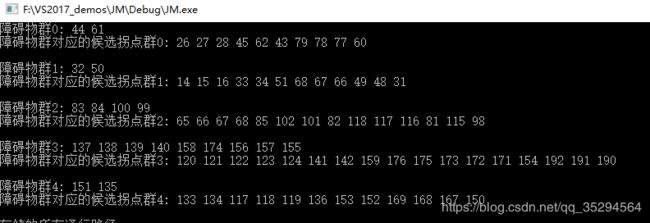
			cout << "障碍物群" << Q_num << ": ";
			for (int j = 0; j < numSize&&BlockQ[j]; j++) {
				points[BlockQ[j]-1].BlockQ_num = Q_num;
				cout << BlockQ[j] << " ";
			}
			cout << endl;
			/**************************************************************/
			cout << "障碍物群对应的候选拐点群" << Q_num << ": ";
			for (int j = 0; j < numSize&&P_Guais[j]; j++) {
				cout << P_Guais[j] << " ";
			}
			cout << endl << endl;
			/**************************************************************/
			for (int k = 0; k < numSize && P_Guais[k]; k++) {
				P_GuaisQ[Q_num][k] = P_Guais[k];
			}
			Q_num++;
		}
		
	}
	//cout << points[134].BlockQ_num << endl;

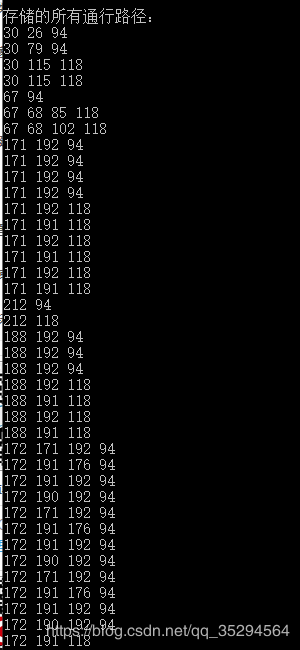
	cout << "存储的所有通行路径：" << endl;
	int Paths[1000][4] = {0};
	int paths = 0;
	bool oneFlag = true;
	bool direct = true;
	bool flag = true;
	for (int i = 0; i < numSize&&Port[i]; i++) {//遍历所有直连路径判断与所有障碍物的关系
		for (int j = 0; j < numSize&&Target[j]; j++) {
			direct = true;
			for (int k = 0; k < numSize&&Block[k]; k++) {
				oneFlag = false;
				
				if (isCrash(Block[k], Port[i], Target[j])) {
					direct = false;

					//P_Guais[100] = { 0 };
					//for (int kk = 0; kk < Width*Height; kk++) {
					//	if(!points[kk].isBlock)
					//		points[kk].searchFlag = false;//非障碍物的地方访问标志重置
					//}
					//findP_Guai(Block[k]);

					P_Guais[100] = { 0 };
					for (int i = 0; i < 100; i++) {
						P_Guais[i] = P_GuaisQ[points[Block[k] - 1].BlockQ_num][i];
					}
					
					for (int t = 0; t < numSize && P_Guais[t]!=0; t++) {
						flag = true;
						for (int ki = 0; ki < numSize&&Block[ki]; ki++) {

							if (isCrash(Block[ki], Port[i], P_Guais[t]) || isCrash(Block[ki], P_Guais[t], Target[j])) {
								flag = false;
							}
						}
						if (flag) {
							Paths[paths][0] = Port[i];
							Paths[paths][1] = P_Guais[t];
							Paths[paths][2] = Target[j];
							cout << Paths[paths][0] << " " << Paths[paths][1] << " " << Paths[paths][2] << endl;
							paths++;
							oneFlag = true;
						}
					}
					if (!oneFlag) {//找存在两个转折点的路径
						for (int m = 0; m < numSize&&P_Guais[m]; m++) {
							for (int n = 0; n < numSize&&P_Guais[n]; n++) {
								bool flag = true;
								for (int ki = 0; ki < numSize&&Block[ki]; ki++) {
									if (isCrash(Block[ki], P_Guais[m], P_Guais[n]) || isCrash(Block[ki], P_Guais[m], Port[i]) || isCrash(Block[ki], P_Guais[n], Target[j])) {
										flag = false;
									}
								}
								if (flag) {
									Paths[paths][0] = Port[i];
									Paths[paths][1] = P_Guais[m];
									Paths[paths][2] = P_Guais[n];
									Paths[paths][3] = Target[j];
									cout << Paths[paths][0] << " " << Paths[paths][1] << " " << Paths[paths][2] << " " << Paths[paths][3] << endl;
									paths++;
								}
							}
						}
					}
				}
			}
			if (direct) {
				Paths[paths][0] = Port[i];
				Paths[paths][1] = Target[j];
				cout << Paths[paths][0] << " " << Paths[paths][1] << endl;
				paths++;
			}
		}
	}
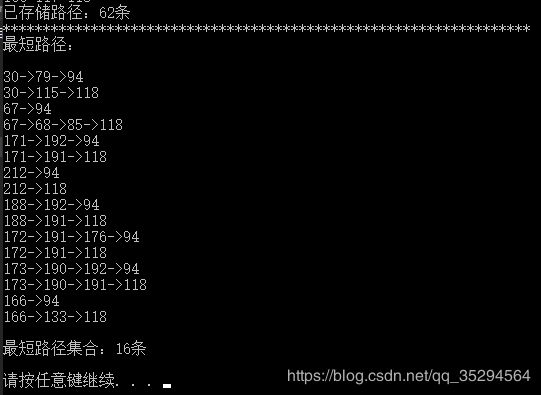
	cout << "已存储路径：" << paths << "条" << endl;
	cout << "******************************************************************" << endl;
	cout << "最短路径：" << endl << endl;

	
	for (int i = 0; i < paths; i++) {
		for (int j = 0; j < 4; j++) {
			if (Paths[i][1] && !Paths[i][2]) {//只有两个数，不需要排序
				;
			}
			if(Paths[i][2] && !Paths[i][3]){//三个数，排序
				if (Paths[i][2] == Paths[i + 1][2] && Paths[i][0] == Paths[i + 1][0]) {
					if (distance(Paths[i][0], Paths[i][1]) + distance(Paths[i][1], Paths[i][2]) > distance(Paths[i + 1][0], Paths[i + 1][1]) + distance(Paths[i + 1][1], Paths[i + 1][2])) {
						//删除Paths[i]
						for (int k = i; k < paths - 1; k++) {
							Paths[k][0] = Paths[k + 1][0];
							Paths[k][1] = Paths[k + 1][1];
							Paths[k][2] = Paths[k + 1][2];
							Paths[k][3] = Paths[k + 1][3];
						}
						paths--;
					}
					else {
						//删除Paths[i+1]
						for (int k = i; k < paths - 2; k++) {
							Paths[k + 1][0] = Paths[k + 2][0];
							Paths[k + 1][1] = Paths[k + 2][1];
							Paths[k + 1][2] = Paths[k + 2][2];
							Paths[k + 1][3] = Paths[k + 2][3];
						}
						paths--;
					}
					i--;
				}
			}
			if (Paths[i][3]) {//四个数，排序
				if (Paths[i][3] == Paths[i + 1][3] && Paths[i][0] == Paths[i + 1][0]) {
					if (distance(Paths[i][0], Paths[i][1]) + distance(Paths[i][1], Paths[i][2]) + distance(Paths[i][2], Paths[i][3]) > distance(Paths[i + 1][0], Paths[i + 1][1]) + distance(Paths[i + 1][1], Paths[i + 1][2]) + distance(Paths[i + 1][2], Paths[i + 1][3])) {
						//删除Paths[i]
						for (int k = i; k < paths - 1; k++) {
							Paths[k][0] = Paths[k + 1][0];
							Paths[k][1] = Paths[k + 1][1];
							Paths[k][2] = Paths[k + 1][2];
							Paths[k][3] = Paths[k + 1][3];
						}
						paths--;
					}
					else {
						//删除Paths[i+1]
						for (int k = i; k < paths - 2; k++) {
							Paths[k + 1][0] = Paths[k + 2][0];
							Paths[k + 1][1] = Paths[k + 2][1];
							Paths[k + 1][2] = Paths[k + 2][2];
							Paths[k + 1][3] = Paths[k + 2][3];
						}
						paths--;
					}
					i--;
				}
			}
		}
	}
	paths++;
	for (int i = 0; i < paths; i++) {
		for (int j = 0; j < 4 && Paths[i][j]; j++) {
			cout << Paths[i][j];
			if (Paths[i][j+1]&&j<3) {
				cout << "->";
			}
		}
		cout << endl;
	}
	cout << endl << "最短路径集合：" << paths << "条" << endl << endl;
	//cout << "distance" << distance(60, 113) + distance(113, 123) << endl;
	//cout << "distance" << distance(60, 82) + distance(82, 123) << endl;
	system("pause");
	return 0;
}

 结果输出：