游戏人工智能之A *寻路算法(适合初学者)

引言：小生今日分享的是寻路系统中常用的A*寻路算法，在此特别感谢Siki学院的老师们。

如果大神发现错误，请评论告知！再次感谢！

开发版本：unity 2017.1.1f1

适合人群：Unity有一定基础的童鞋

开启学习之旅吧！

寻路：寻找最短路径并避开障碍物

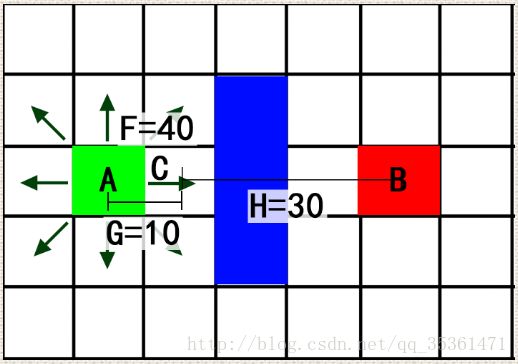
首先将地图虚拟化，将地图划分为一个一个的小方块，这样可以用二维数组来表示地图。如下所示，绿色块(A)是起点，红色块(B)是终点，中间蓝色块是障碍物，白色块是空地。

先罗列出所有的步骤，等会按照例子一步一步分析

1 寻路步骤：

步骤1.从起点A开始，把A作为一个等待检查的方格，放入到“开启列表”中，开启列表就是一个存放等待检车方格的列表

步骤2.寻找起点A周围可以到达的方格（最多八个），将它们放入到“开启列表”，并设置它们的父方格为A

步骤3.从“开启列表”中删除点A,并将A放入到“关闭列表”中，“关闭列表”存放的是不再需要检查的方格

步骤4.计算每个方格的F值

F=G+H:

G 表示从起点A移动到指定方格的移动消耗，我们假设横向移动一个格子消耗10，斜向移动一个格子消耗14（具体值可以根据情况修改）

H 表示从指定的方格移动到目标B点的预计消耗，我们假设H的计算方法，忽略障碍物，只可以纵横向计算

步骤5.从“开启列表”中选择F值最低的方格C，将其从“开启列表”中删除，放入到“关闭列表”中

步骤6.检查C所有临近并且可达的方格（障碍物和“关闭列表”中的方格不考虑），如果这些方格还不在“开启列表”中的话，将它们加入到开启列表，并且计算这些方格的F值，并设置父方格为C。

步骤7.如果某相邻的方格D已经在“开启列表”，计算新的路径从A到达方格D（即经过C的路径），G值是否更低一点，如果新的G值更低，则修改父方格为方格C，重新计算F值，H值不需要改变，因为方格到达目标点的预计消耗是固定的。但如果新的G值比较高，则说明新的路径消耗更高，则值不做改变。

步骤8.继续从“开启列表”中找出F值最小的，从“开启列表”中删除，添加到“关闭列表”，再继续找出周围可以到达的方块，如此循环

步骤9.当“开启列表”中出现目标方块B时，说明路径已经找到。除了起始方块A，每一个曾经或者现在还在“开启列表”中的方块，都存在一个“父方格”，可以从目标点B通过父方格索引到起始方块，这就是路径。

2 案例分析：

步骤1,2,3：方块A已经放入到“关闭列表”，周围临近的8个方格（没有障碍物）已经放入到“开启列表”

步骤4：计算F=G+H

以方格C为例

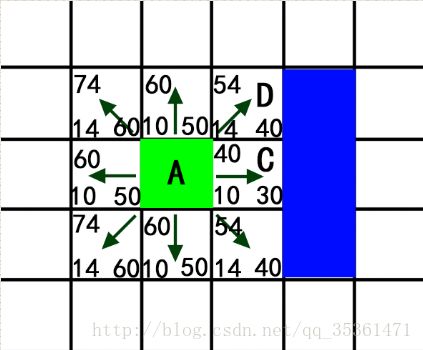
为了方便统计，将左上角数字记为F值，左下角为G值，右下角为H值，则如下所示：（箭头的起点为该方格的父方格）

步骤5，6：我们发现C的F值最小，将其从“开启列表”中移除，加入到“关闭列表”中。C右边三个是障碍物不考虑，左边起始方块A已经加入到“关闭列表”，不考虑。则候选的方块也只有上下四个:，而且也已经存在“开启列表”中。

步骤7：从开启列表中找出F最小的，我们发现上下两个同为54，取哪个都可以，选择上面的方格D。

重新计算G值，路径A-C-D 计算G值为20，比原来的A-D路径的G值14要大，则值不变，方格D的父方格不变。

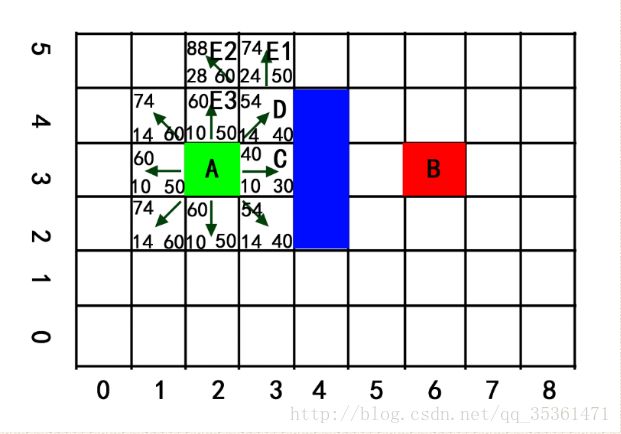
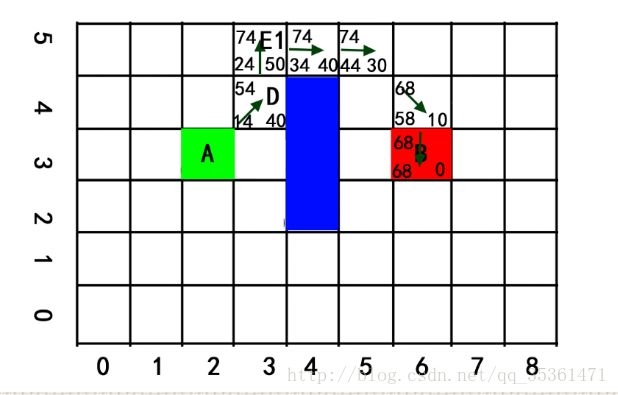
步骤8：跳到步骤5开始，选择F值最小的D，将其从“开启列表”中移除，加入到“关闭列表”中。将周围可达方格加入到“开启列表”并计算F值

我们规定如果上下左右有障碍物，则对应的右上，右下，左上，左下不可到达，所以方格D右上角不可到达。将可到达的方格E1,E2加入“开启列表”，计算F值，然后再比较到达周围方格的G值是否存在更小值，最后发现 “开启列表”里F最小的方格是E3方格，然后再次跳到步骤5，继续执行。。。

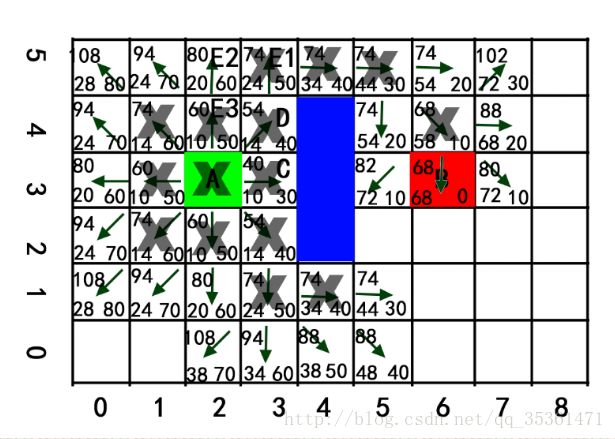
步骤9：当循环15遍后，如下图所示（图画得快吐了，其中打叉的方格表示在“关闭列表”中），目标方块B出现在“开启列表”中，结束循环！

通过目标点B的父方格索引到起始方块A，这就是路径,如下所示：

本篇主要介绍A*寻路算法的思路，下一篇，将会在Unity中实现寻路算法！

博客写之不易，喜欢的，记得点赞收藏，关注我哦!