PyTorch理解更多神经网络优化方法
了解不同优化器
SGD
随机梯度下降法是梯度下降法的一个小变形,就是每次使用一批(batch) 数掘进行梯度的计算,而不是计算全部数据的梯度.因为现在深度学习的数据量都特别大, 所以每次都计算所有数据的梯度是不现实的,这样会导致运算时间特别长,同时每次都计
算全部的梯度还失去了一些随机性, 容易陷入局部误差,所以使用随机梯度下降法可能每次都不是朝着真正最小的方向.但是这样反而容易跳出局部极小点。
Momentum
第二种优化方法就是在随机梯度下降的同时,增加动量(Momentum) 。这来自于物理中的概念, 可以想象损失函数是一个山谷,一个球从山谷滑下来,在一个平坦的地势,球的滑动速度就会慢下来,可能陷入一些鞍点或者局部极小值点。这个时候给它增加动量就可以让它从高处滑落时的势能转换为平地的功能,相当于惯性增加f小球在平地滑动的速度,从而帮助其跳出鞍点或者局部极小点。动量的计算基于前面梯度,也就是说参数更新不仅仅基于当前的梯度,也基于之前的梯度。

通俗地说,梯度下降的方向是由这一点的方向导数决定的,如果我们考虑小球的惯性,除了这个点上的梯度会决定下一次的前进方向外,上一次前进方向由于惯性也会影响下一次的前进方向,这样两个方向的合力生成下一次小球的加速度。
Adagrad
公式是这样的
w t + 1 ← w t − η ∑ i = 0 t ( g i ) 2 + ϵ g t w^{t+1} \leftarrow w^{t}-\frac{\eta}{\sqrt{\sum_{i=0}^{t}\left(g^{i}\right)^{2}}+\epsilon} g^{t} wt+1←wt−∑i=0t(gi)2+ϵηgt
有种在线更新参数的感觉,我们可以看到学习率在不断变小, 且受每次计算出来的梯度影响,对于梯度比较大的参数,它的学习率就会变得相对更小,里面的根号特别重要,没有这个根号算法表现非常差。 ϵ {\epsilon} ϵ是一个平滑参数,通常设置为 1 0 − 4 − 1 0 − 8 10^{-4} -10^{-8} 10−4−10−8,同时为了避免分母为0。
自适应学习率的缺点就是在某些情况下一直递减的学习率并不好,这样会造成学习过早停止。
RMSprop
公式是这样的
cache t = α ∗ cache t − 1 + ( 1 − α ) ( g t ) 2 \operatorname{cache} ^{t}=\alpha * \operatorname{cache} ^{t-1}+(1-\alpha)\left(g^{t}\right)^{2} cachet=α∗cachet−1+(1−α)(gt)2
w t + 1 ← w t − η cache t + ϵ g t w^{t+1} \leftarrow w^{t}-\frac{\eta}{\sqrt{\operatorname{cache} ^{t}+\epsilon}} g^{t} wt+1←wt−cachet+ϵηgt
这里多了一个 α \alpha α,这是一个衰减率,也就是说RMSprop 不再会将前面所有的梯度平方求和,而是通过一个衰减率将其变小,使用了一种滑动平均的方式,越靠前面的梯度对自适应的学习率影响越小,这样就能更加有效地避免Adagrad 学习率一直递减太多的问题,能够更快地收敛。
Adam
这是一种综合型的学习方法,可以看成是RMSprop 加上动量(Momentum) 的学习方法,达到比RMSProp 更好的效果。
书写优化器代码
- Momentum
- 二维优化,随机梯度下降法进行优化实现
- Ada自适应梯度调节法
- RMSProp
- Adam
- PyTorch种优化器选择
SGD
import torch.nn.functional as F
import torch.nn.init as init
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import numpy as np
import math
%matplotlib inline
#梯度下降法
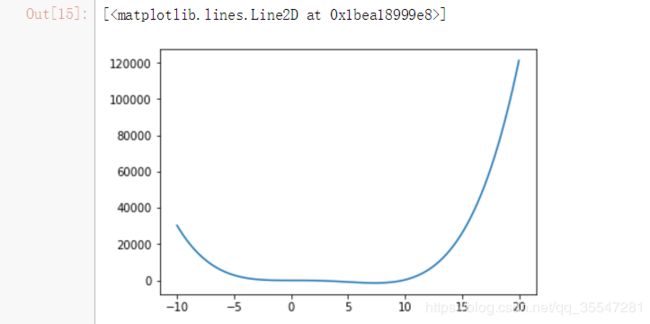
J=lambda w:1.5*w**4 - 15*w**3 + 3*w**2#创建一个较为复杂的函数
J_prime = lambda w:(6*w**3-45*w**2+6*w)*(1+10*np.random.random())
#在J函数导数后面加上了额一个噪声是为了模拟随机梯度下降
#随机梯度下降是每一次在数据里随机选取若干样本得到的梯度
w=np.linspace(-10,20,100)
plt.plot(w,J(w))#将结果画出来,w和dJ(w)/dw
#通过将梯度进行累加求平均可以解决噪声带来的影响,但是这样求平均并不是最优的方法
J=0
for i in range(100):
J += J_prime(1)
J/100
np.random.random()
#生成随机浮点数,取值范围:[0,1)
这是从0-100之间模拟SGD,并且画出Loss.
#梯度下降法
w=1
epoch=100
lr=0.001
Loss=[]
W=[]
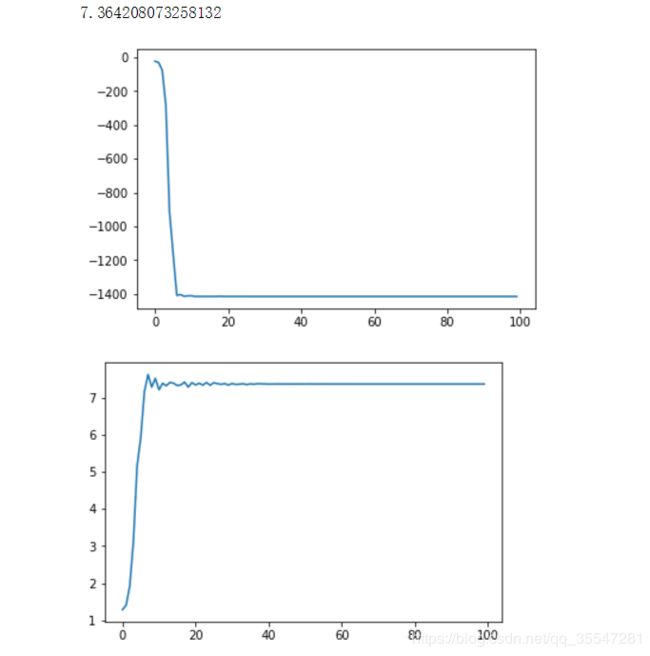
for i in range(epoch):
w=w-lr*(J_prime(w))#更新梯度
Loss.append(J(w))
W.append(w)
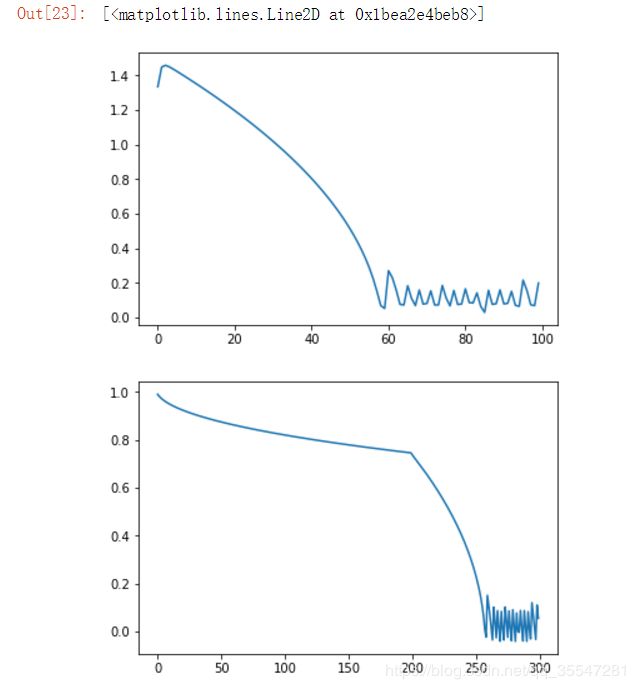
plt.plot(Loss)
plt.figure()
plt.plot(W)
print(w)
Momentum
#动量算法,我们希望每次累加的量但是更加重视当下的梯度,因此要做一个随着时间变化的加权平均
J=0
JJ=[]#用来记录梯度的值
for i in range(1000):
J=0.9*J+0.1*J_prime(1)
#我们对当下的梯度赋予一个权重,J_prime是当下梯度
JJ.append(J)
plt.plot(JJ)
#动量梯度下降法,一定要初始化v
w=1
epoch=100
lr=0.001
beta=0.5
y=[]
v=0
Loss=[]
W=[]
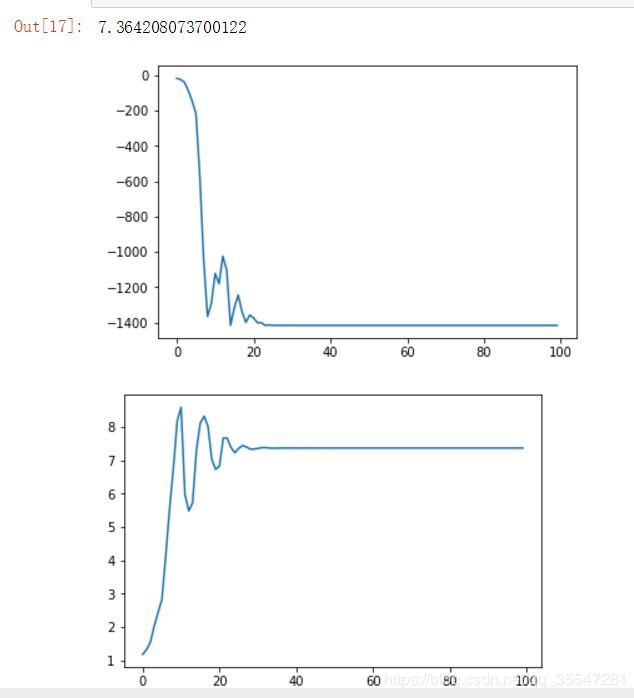
for i in range(epoch):
v=beta*v + (1-beta)*J_prime(w)
#第一次的梯度是没有的,所以初始化为0,beta控制两次梯度的权重来合成新的梯度
w=w-lr*v
#用v进行梯度更新
Loss.append(J(w))
W.append(w)
plt.plot(Loss)
plt.figure()
plt.plot(W)
w
#二维情况下的随机梯度下降
J = lambda w1,w2: w1**2 + 10*w2**2
#是一个椭圆函数,w1和w2的初值差异比较大
J_prime1 = lambda w1: 2*w1
J_prime2 = lambda w2:20*w2
#设初值
w1 = 1
w2 = -1
epoch = 200
lr = 0.01
y = []
v = 0
s = 0
Loss = []
W1 = []
W2 = []
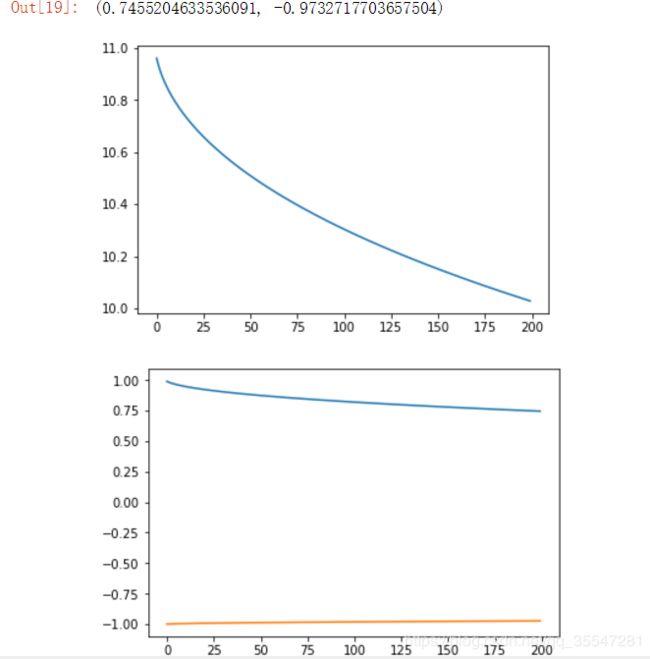
for i in range(epoch):
w1 = w1 - lr*(J_prime1(w1))
w2 = w2 - lr*(J_prime2(w2))
W1.append(w1)
W2.append(w2)
Loss.append(J(w1,w2))
plt.plot(Loss)
plt.figure()
plt.plot(W1)
plt.plot(W2)
w1,w2
Adagrad
#Ada自适应梯度调节法,为了解决两个参数优化是差异过大存在的问题,调节不同方向上梯度变化
J = lambda w1,w2: w1**2 + 10*w2**2
#是一个椭圆函数,w1和w2的初值差异比较大
J_prime1 = lambda w1: 2*w1
J_prime2 = lambda w2:20*w2
#设初值
w1 = 1
w2 = -1
epoch = 200
lr = 0.01
y = []
v = 0
s = 0
Loss = []
W1 = []
W2 = []
s1 = s2 = 0
for i in range(epoch):
s1 += J_prime1(w1)**2
w1 = w1 - lr*(J_prime1(w1)/np.sqrt(s1))
#大的梯度变化会除以更大的归一化因子
s2 += J_prime2(w2)**2
w2 = w2 - lr*(J_prime1(w2)/np.sqrt(s2))
W1.append(w1)
W2.append(w2)
Loss.append(J(w1,w2))
plt.plot(Loss)
plt.figure()
plt.plot(W1)
plt.plot(W2)
w1,w2
#引入动量的思想
s = 0
S = []
beta = 0.8
for i in range(100):
s = 0.2*s + 0.8*J_prime1(w1)**2
S.append(np.sqrt(s))
w1 = w1 -lr*(J_prime1(w1)/s)
W1.append(w1)
plt.plot(S)
plt.figure()
plt.plot(W1)
RMSProp
J = lambda w1,w2: w1**2 + 10*w2**2
#是一个椭圆函数,w1和w2的初值差异比较大
J_prime1 = lambda w1: 2*w1
J_prime2 = lambda w2: 20*w2
#设初值
w1 = 1
w2 = -1
epoch = 200
lr = 0.01
beta2 = 0.5
y = []
v = 0
s = 0
Loss = []
W1 = []
W2 = []
s1 = s2 = 0
for i in range(epoch):
s1 = beta2*s1 + (1-beta2)*(J_prime1(w1)**2)#引入动量的思想
s1_correct = s1/(1-beta2**(i+1))#s1_correct随时间变化的函数
w1 = w1 - lr*(J_prime1(w1)/np.sqrt(s1))
s2 = beta2*s2 + (1-beta2)*(J_prime1(w2)**2)
s2_correct = s2/(1-beta2**(i+1))
w2 = w2 - lr*(J_prime1(w2)/np.sqrt(s2))
W1.append(w1)
W2.append(w2)
Loss.append(J(w1,w2))
plt.plot(Loss)
plt.figure()
plt.plot(W1)
plt.plot(W2)
w1,w2
Adam
在这里我们就能看出Adam就是RSMProp和Momentum的结合,先对梯度和冲量结合,再根据大小修正
#一维情况
J=lambda w:1.5*w**4 - 15*w**3 + 3*w**2#创建一个较为复杂的函数
J_prime = lambda w:(6*w**3-45*w**2+6*w)*(1+10*np.random.random())
w = 1
epoch = 200
lr = 0.1
beta1 = 0.9
beta2 = 0.99
y = []
v = 0
s = 0
Loss = []
W = []
for i in range(epoch):
v = beta1*v + (1-beta1)*J_prime(w)
v_correct = v/(1-beta1**(i+1))
s = beta2*s + (1-beta2)*(J_prime(w)**2)
s_correct = s/(1-beta2**(i+1))
w = w - lr*(v/np.sqrt(s))
W.append(w)
Loss.append(J(w))
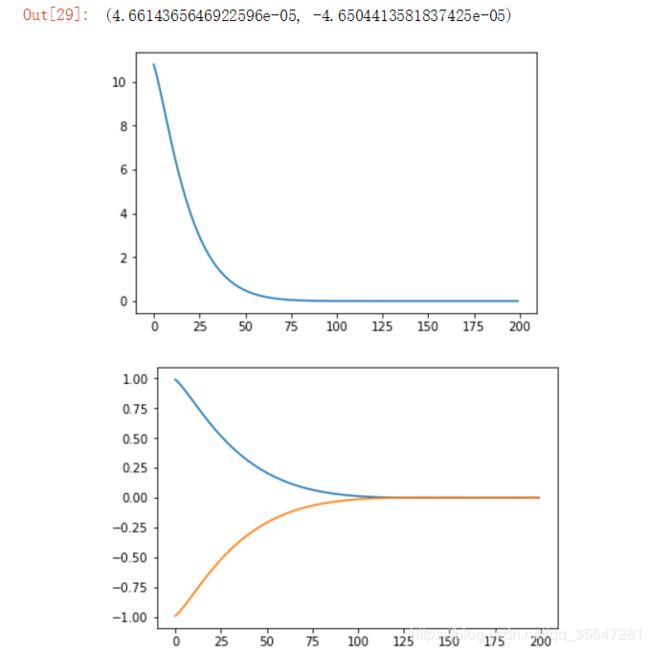
plt.plot(Loss)
plt.figure()
plt.plot(W)
w
#二维情况
J = lambda w1,w2: w1**2 + 10*w2**2
J_prime1 = lambda w1: 2*w1
J_prime2 = lambda w2: 20*w2
w1 = 1
w2 = -1
epoch = 200
lr = 0.01
beta1 = 0.9
beta2 = 0.99
y = []
v1 = v2 = 0
s1 = s1 = 0
Loss = []
W1 = []
W2 = []
for i in range(epoch):
v1 = beta1*v1 +(1-beta1)*J_prime1(w1)
v1_correct = v1/(1 - beta1**(i+1))
s1 = beta2*s1 +(1-beta2)*(J_prime1(w1)**2)
s1_correct = s1/(1 - beta2**(i+1))
w1 = w1 - lr*(v1/np.sqrt(s1))
v2 = beta1*v2 +(1-beta1)*J_prime1(w2)
v2_correct = v2/(1 - beta1**(i+1))
s2 = beta2*s2 +(1-beta2)*(J_prime1(w2)**2)
s2_correct = s2/(1 - beta2**(i+1))
w2 = w2 - lr*(v2/np.sqrt(s2))
W1.append(w1)
W2.append(w2)
Loss.append(J(w1,w2))
plt.plot(Loss)
plt.figure()
plt.plot(W1)
plt.plot(W2)
w1,w2
用PyTorch实现
import torch.nn.functional as F
import torch.nn.init as init
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import numpy as np
import math
%matplotlib inline
#%matplotlib inline 可以在Ipython编译器里直接使用
#功能是可以内嵌绘图,并且可以省略掉plt.show()这一步。
xy=np.loadtxt('./data/diabetes.csv.gz',delimiter=',',dtype=np.float32)
x_data=torch.from_numpy(xy[:,0:-1])#取除了最后一列的数据
y_data=torch.from_numpy(xy[:,[-1]])#取最后一列的数据,[-1]加中括号是为了keepdim
print(x_data.size(),y_data.size())
#print(x_data.shape,y_data.shape)
#建立网络模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.l1=torch.nn.Linear(8,6)
self.l2=torch.nn.Linear(6,4)
self.l3=torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self,x):
out1=self.sigmoid(self.l1(x))
out2=self.sigmoid(self.l2(out1))
y_pred=self.sigmoid(self.l3(out2))
return y_pred
#our model
model=Model()
criterion=torch.nn.BCELoss(size_average=True)
#optimizer=torch.optim.SGD(model.parameters(),lr=0.1),正常的梯度下降
#optimizer=torch.optim.SGD(model.parameters(),lr=0.1,momentum=0.9),带动量比列的梯度下降
#Adam
optimizer=torch.optim.Adam(model.parameters(),lr=0.05,betas=(0.9,0.999),weight_decay=0.001)
#training loop
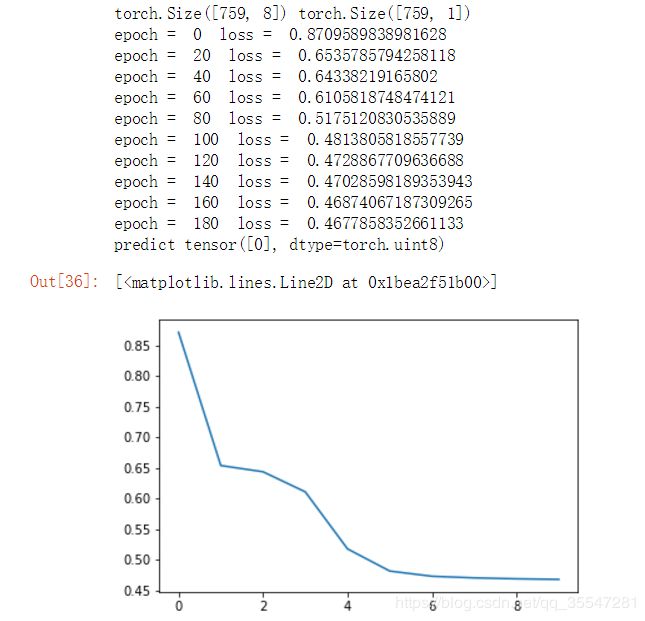
Loss=[]
for epoch in range(200):
y_pred=model(x_data)
loss=criterion(y_pred,y_data)
if epoch%20 == 0:
print("epoch = ",epoch," loss = ",loss.data.item())
Loss.append(loss.data.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
hour_var = Variable(torch.randn(1,8))
print("predict",model(hour_var).data[0]>0.5)
plt.plot(Loss)