金融时间序列Note 1 —— 平稳性，相关系数，自相关函数(ACF)及其平稳性检验

本文用于《金融时间序列》的相关介绍，适合快速入门和期末复习。（才怪我感觉自己考的超烂）

OK，首先用自己的话讲一下什么是时间序列，首先我们会考得最多得时间序列肯定是线性的，既然说了有线性的，那肯定就有非线性的，经典的三类AR,MA,ARMA。那什么是时间序列呢？首先这是一个数学模型，用来干嘛？用来做预测的，举个例子，如果你知道一个月之后某只股票的股价，你是不是发达了，那你怎么预测呢？猜数字？不可能吧，一般你会怎么做？当然就是先去看看过去半年这个股票的趋势是怎么样的，是一直升还是一直跌，还是升升又跌跌，总而言之，它就是利用过去的这支股票的信息来预测它之后的价格。理解了之后，我们就明白，噢，线性的时间序列就是你要预测的价格就是过去的一些价格的线性组合，这样是不是就很好理解了。

作为一门数学模型，当然就需要一些严格的前提，什么样的数据可以用时间序列来预测呢？因此首先要讲讲平稳性的概念。

首先我们要明确一点，每个时间点上的股票价格都应该被视为一个随机变量，简单说就是它服从某个分布，落入（被确定为）某些值的概率是有规律的。

既然是随机变量，那这么多天的价格，就是一群随机变量了，那我们如果能求出它们的联合分布，那不就美滋滋（因为过去的价格已知，代入求解就可以），显然它们也不可能是独立的，独立的还预测个毛啊，独立的话前面的价格和后面的价格根本没关系啊喂！既然扯到联合分布，就可以介绍严平稳的概念了，严平稳就是之前我们不是说一群随机变量嘛？但是我们并没有给出一群是多少个，现在我们规定是k个，换成股票来说就是k天的股票价格，换成我自己的理解就是时间轴上面，一个点是一天的价格，k天的价格便是一个线段，这个线段在时间轴上滑动是，对应的价格的联合分布不变，这就是严平稳。

给出的准确定义是：$r_{t_i}$代表$t_i$时刻下的价格这个随机变量，t是你滑动的距离
$F(r_{t_1},r_{t_2},...,r_{t_k})=F(r_{t_1+t},r_{t_2+t},r_{t_k+t})$

严平稳是很强的条件，能不能放宽松一点呢，于是出现了宽平稳，也叫弱平稳。定义是，$r_t$的均值、$r_t$和$r_{t-l}$的协方差不随时间的变化而变化，从直观上理解，我们要求一段段时间价格的分布是不变的，大部分情况下，这个严格要求相同的条件，必然包含了弱平稳所要求的条件，出于要求的放宽，我们要求均值要一致，个个时间点上的差异只和距离有关。

准确的定义是：
(1)$E(r_t)=\mu$
(2)$Cov(r_t,t_{t-l})={\gamma }_l$，$l$是间隔距离

之前我们说过大部分情况下严平稳是可以推出弱平稳的，其实有一种情况要例外，就是我们还要求$r_t$的一阶矩和二阶矩是有限的，加上这个条件严平稳完全可以推出弱平稳。

反之，弱平稳能不能推出严平稳呢？答案是可以的，但是要求很过分，我们必须要求$r_t$是服从正态分布的。证明书中并没有给出，所以应该是比较复杂的，大家记住结论即可。

定义(2)$Cov(r_t,t_{t-l})={\gamma }_l$，可以推出一下性质。
(a)${\gamma }_0=Var(r_t)$
(b)${\gamma }_{-l}={\gamma }_l$
性质(b)是因为$Cov(r_t,r_{t+l})=Cov(r_{t+l},r_t)$，协方差互换位置不变，

OK，接下来介绍相关系数，其实就是按我的理解就是标准化协方差。
直接给出定义：
${\rho }_{x,y}=\frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}}=\frac{E\left[\left(X-{\mu }_x\right)\left(Y-{\mu }_y\right)\right]}{\sqrt{E{\left(X-{\mu }_x\right)}^{2}E{\left(Y-{\mu }_y\right)}^2}}$
重要性质说两点：
(1)$\rho \in [-1,1]$
(2)${\rho }_{x,y}={\rho }_{y,x}$
作用${\rho }_{x,y}=0$，两儿随机变量不相关，不相关和独立还是不一样的，只有当正态的时候才是等价的。

OK，老生常谈的问题，这玩儿意是分布本身的啊，我们只有样本咋子去估计它捏？
一样的，不就不知道两均值嘛，直接样本均值代替了不就完事儿了
${\hat{\rho }}_{x,y}=\frac{{\sum }_{t=1}^T\left(x_t-\overline{x}\right)\left(y_t-\overline{y}\right)}{\sqrt{{\sum }_{t=1}^T{\left(x_t-\overline{x}\right)}^2{\sum }_{t=1}^T{\left(y_t-\overline{y}\right)}^2}}$

OK，这是数理统计上的概念，换到时间序列上该咋整捏？
这玩儿意就变成了ACF，自相关函数，把$r_t$和$r_{t-l}$的相关系数称为时间间隔为$l$的自相关系数。
${\rho }_{\ell }=\frac{\mathrm{Cov}\left(r_t,r_{t-\ell }\right)}{\sqrt{\mathrm{Var}\left(r_t\right)\mathrm{Var}\left(r_{t-\ell }\right)}}=\frac{\mathrm{Cov}\left(r_t,r_{t-\ell }\right)}{\mathrm{Var}\left(r_t\right)}=\frac{{\gamma }_{\ell }}{{\gamma }_0}$
如果这数据是弱平稳的$Var(r_t)=Var(r_{t-l})$，因为协方差只和$l$有关嘛，$l=0$的时候就是方差
同样面临咋子估计的问题
走你，就是根据相关系数的估计照葫芦画瓢
${\hat{\rho }}_{\ell }=\frac{{\sum }_{t=\ell +1}^T\left(r_t-\overline{r}\right)\left(r_{t-\ell }-\overline{r}\right)}{{\sum }_{t=1}^T{\left(r_t-\overline{r}\right)}^2},0\le \ell <T-1$

先讲到这里叭，下周给大家总结一下检验的问题。
大家好，我又回来了，给观众老爷们继续讲讲ACF的检验。

首先我们要回顾一下我们之前说的弱平稳的概念，肥肠简单，两条公式：
(1)$E(r_t)=\mu$
(2)$Cov(r_t,t_{t-l})={\gamma }_l$，$l$是间隔距离

我们一直要求数据一定要弱平稳，弱平稳，到底弱平稳有什么好处呢？
弱平稳的第一条，均值相同，首先要求这些个随机变量的大概率会在$\mu$值附近，这样我们才有相似性，因为如果你的$r_t$均值在0，你的$r_{t-1}$均值在1000000000000000000000000，你觉得能用$r_{t-1}$去预测$r_t$吗？
第二我们要求协方差只和间隔距离有关，说明什么，你用前k步去预测下一步的值这种模式对任意的时间点都是一样的，也就是说你用$r_1$预测$r_2$同样可以用$r_2$预测$r_3$。

OK，既然弱平稳是我们的必要前提，怎么验证数据是不是弱平稳呢？
首先介绍一下大名鼎鼎的Bartlett公式

若$r_t$是一个弱平稳序列，且满足$r_t=\mu +{\sum }_{i=0}^q{\psi }_i{a}_{t-i}$（为什么要长成这样呢？在文章最后我会介绍，等不及的朋友可以先划到去看），其中${\psi }_0=1$，{$a_j$}是均值为0的独立同分布任意变量的序列，则对于$l>q$，${\hat{\rho }}_{\ell }$渐进服从均值为0、方差为$\left(1+2{\sum }_{i=1}^q{\rho }_i^2\right)/T$的正态分布。

有了这个正态分布，我们自然就可以想到做假设检验，最基础的用一个t统计量来做

$t\text{-ratio}=\frac{{\hat{\rho }}_{\ell }}{\sqrt{\left(1+2{\sum }_{i=1}^{\ell -1}{\hat{\rho }}_i^2\right)/T}}$

t-ratio在$H_0:{\rho }_l=0$下渐进服从标准正态分布，因此双边检测，只要$|t\text{ ratio }|>Z_{\alpha /2}$时拒绝H0.

如果是检验多个${\rho }_i$呢？这时候就需要Ljung-Box Test，用到的统计量是$Q(m)$

$Q(m)=T(T+2){\sum }_{\ell =1}^m\frac{{\hat{\rho }}_{\ell }^2}{T-\ell }$

$Q(m)$渐进服从自由度为m的卡方分布，当$Q(m)>{\chi }_{\alpha }^2$时，拒绝$H_0:{\rho }_1=\cdots ={\rho }_m=0$

以上是利用假设检验的方法来做平稳性的判断，ACF本身其实还可以做图像上直观的平稳性检验。
我们把${\hat{\rho }}_1,{\hat{\rho }}_2,\dots$称为$r_t$的样本自相关函数(ACF)
事实上如果ACF的值在两个标准差内，我们就可以认为在5%的水平下它们和0没有显著差别


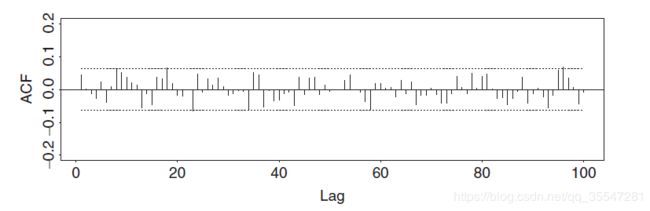
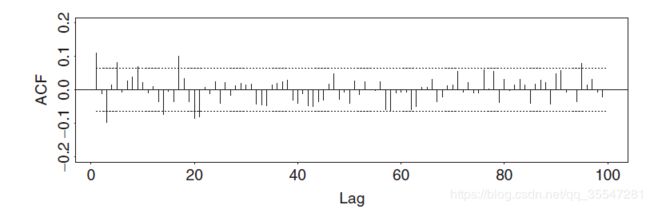
以上两幅图就可以看到第一幅没有序列相关性，而第二幅具有序列相关性。

时间序列里面有一个非常重要的东西叫做白噪声，可以说学习线性时间序列其实就是白噪声的线性组合从入门到放弃，白噪声其实就是具有有限均值和有限方差的独立同分布的随机变量序列。

为什么在bartlet公式里面$r_t$要有那种形式，因为线性的时间序列的定义就是：
$r_t=\mu +{\sum }_{i=0}^{\infty }{\psi }_i{a}_{t-i}$
{$a_t$}是零均值独立同分布的随机变量序列，我们观察一下这种序列的性质：
(1)$E\left(r_t\right)=\mu$
(2)$\mathrm{Var}\left(r_t\right)={\sigma }_a^2{\sum }_{i=0}^{\infty }{\psi }_i^2$
其中${\sigma }_a=Var(a_t)$，由于$\mathrm{Var}\left(r_t\right)<\infty$，所以$\left\{{\psi }_i^2\right\}$一定要收敛，也就是说随着$i$增大，$a_{t-i}$对$r_t$的影响会越来越小。
自协方差：
${\gamma }_{\ell }=\mathrm{Cov}\left(r_t,r_{t-\ell }\right)=E\left[\left({\sum }_{i=0}^{\infty }{\psi }_i{a}_{t-i}\right)\left({\sum }_{j=0}^{\infty }{\psi }_j{a}_{t-\ell -j}\right)\right]$
$=E\left({\sum }_{i,j=0}^{\infty }{\psi }_i{\psi }_j{a}_{t-i}{a}_{t-\ell -j}\right)$
这一步是因为下标不相同的$a_t$因为相互独立，乘积的期望等于期望的乘积，而单独的期望值是0，因此只要挑出那些下标相同的$a_t$
$={\sum }_{j=0}^{\infty }{\psi }_{j+\ell }{\psi }_{j}E\left(a_{t-\ell -j}^2\right)={\sigma }_a^2{\sum }_{j=0}^{\infty }{\psi }_j{\psi }_{j+\ell }$