CIKM'2017 最佳论文鉴赏

写在前面

背景

感谢组织，让我有幸参加了11月初在新加坡举办的ACM CIKM 2017。CIKM全称是Conference on Information and Knowledge Management，是国际计算机学会（ACM）主办的数据库、知识管理、信息检索领域的重要学术会议。

我有几张阿里云幸运券分享给你，用券购买或者升级阿里云相应产品会有特惠惊喜哦！把想要买的产品的幸运券都领走吧！快下手，马上就要抢光了。

今年的Best Paper Award由清华大学的李国良老师团队获得，论文题为：Hike: A Hybrid Human-Machine Method for Entity Alignment in Large-Scale Knowledge Bases《一种基于人机协作的大型知识图谱对齐方法》. 因为是Best Paper，本篇分享单独对该文章做细致解读。为了能让读者有所得，涉及的细节较多，篇幅较长。如果你只是想一瞥论文思路，并不打算深究细节，那么后续Section中只挑“快读”部分阅读即可。

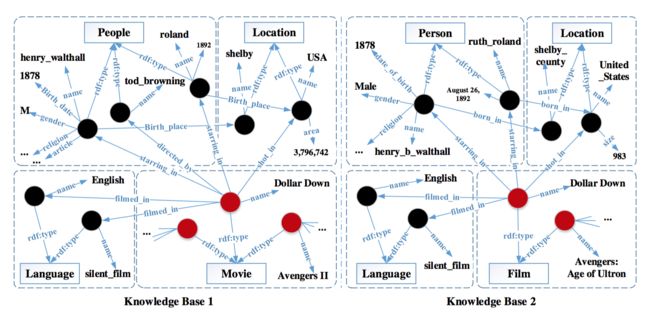
知识库是对客观世界的事物及其相互关系的一种形式化描述(包括实体、类和关系等，下图是2个知识库的示例，圆圈表示实体，实线矩形表示类，实体之间的箭头表示关系)，其目的是让机器像人一样能够记忆、理解、推理，在知识管理、信息检索等领域具有广泛应用。目前很多国内外企业和高校已经建立数百个大型知识库（例如谷歌的Freebase等）。为了提高知识库的覆盖率和准确率，一个重要的任务是集成这些异构知识库。然而，由于这些知识库体量大、不一致性和不确定性高，目前自动化的知识库对齐方法质量不高，召回率低。 文章提出一种新型的人机协作的方法（A Hybrid Human-Machine Method），解决大规模知识库（Knowledge Base）之间实体对齐（Entity Alignment）的问题，并拿到了优于已有的自动对齐方法的结果。实体对齐是知识库对齐的一个子任务，是要判断两个知识库  K K 和  K′ K′ 中，哪些实体描述的是同样的东东，并把它们link起来，例如下图中的hhenry_walthall和henry_b_walthall属于同一实体。

大规模知识库之间的实体对齐问题，有很多挑战：

• 知识库中拥有海量的实体，如果纯靠人工去标记实体并做对齐工作，不论从人工成本还是可行性方面看，都是很不现实的
• 有自动的实体对齐算法，但是召回率只达到70%，质量不高

读后感受

通过仔细地品读整篇文章，个人觉得这个工作之所以能拿下Best Award，原因有如下几个方面：

• 工作内容本身：围绕着“能应用于大规模数据集”这一目标，打出了一系列组合拳，包括实体划分（显著降低计算量，并让问题可并行计算）、偏序构建（使得未知问题的解可通过已知问题的答案推理得到）、问题选择+众包机制+推断算法（进一步降低计算量和花销）和错误容忍机制（提升质量），终使得实体对齐得以在大规模数据集落地。
• 工作非常饱满：几乎每一个细节之处都处理得很精致，不马虎；环环相扣，不断提出问题和解决问题，读后有一种淋漓尽致的感觉。

当然，文章中也存在一些值得商榷的地方和影响阅读的小瑕疵，整体感觉是后半部分质量不及前半部分。但本篇分享不做细节勘误。如果你在细读原论文时有任何细节困惑，欢迎与我交流！

论文解读

下面正式进入对论文细节的解读。为避免概念混淆，请留意：
（1）下文提到的实体对，永远都是指分别来自2个知识库的实体构成的实体对，同一个知识库中不谈实体对。此外，所述实体对只单纯是成对的实体，并不意味着一定是“对齐的”实体。
（2）后文中根据语境，会交叉使用“实体对”和“问题”两种表述，记得它们是一样的东东，因为每个实体对 (ei,ej) (ei,ej)都对应着如下问题：这俩实体是否匹配？

Introduction

符号一览

符号	描述
K K	知识库  K K（Knowledge Base）
(s,p,o) (s,p,o)	K K中的三元组表示

论文背景

随着World Wide Web的发展，有越来越多异构的大规模知识库（Knowledge Base）产生，比如DBPedia（一个从维基百科的词条里撷取出的结构化的知识库）、YAGO（从WordNet和维基百科等构成的知识库）等等。知识库广泛应用于自动问答（Question Answer）、语义搜索（Semantic Search）等领域。知识库有几种组成元素：实体（entity，如Alibaba Group），类（class，实体所属的类别，如Company），关系（relation，如Alibaba Group isA Company，isA即是关系），属性（property），字面值（iteral，如日期、数值等）等。不同的知识库是异构的，因此可以互为补充。例如DBPedia有很多实体（entity）但只有少量的class，而YAGO则拥有成千上万的class（见下表），倘若可以link这两个知识库，便可以起到互相补充以提高知识库覆盖度的作用。

Dataset	#Entity	#Class	#Property
YAGO	3.03M	360K	70
DBPedia	2.49M	0.32K	1.2K

通常，我们会以三元组 (s,p,o) (s,p,o) 表达知识库中的一条条事实：  s=subject s=subject ，可以是实体或类； o=object o=object ，可以是实体、类或字面值；  p=predicate p=predicate （谓词），可以是关系或属性。

先贴一下方案的框架图，可以看到：输入是两个知识库 K K和 K′ K′，输出是两个知识库之间匹配的实体对，主要流程有Entity Partition，Partial Order Construction，Question Selection和Error Tolerance。

接下来，我们看看论文作者是如何环环相扣，以较小的计算量和花销解决实体对齐问题的。

Entity Partition

快读

将大规模知识库切成一个个的小块，目的是使得落在同一个块中的实体对大概率可对齐，而不同块之间的实体则不大可能匹配。作者基于事实观察，创新地以谓词为线索进行切分。通过寻找每个谓词的匹配谓词，并根据谓词与实体的对应关系，便可得到与该谓词对相关的2个实体集，进一步可计算出匹配谓词对的相似度。当拿到所有匹配谓词对的相似度后，即可通过改进的HAC算法完成谓词对的合并，最终得到实体对的切块结果。由于块与块之间不存在重叠，后续判断实体对是否匹配的过程即可在各个块内并发进行，大大降低复杂度。Entity Partition是使得本文所提方法能应用于大规模知识库的重要一步。

读后感受：作者以谓词为线索进行知识库切分，是思路比较创新的地方；另外，对经典的HAC聚类算法做了简单的改进，降低了复杂度，让方法落地成为可能。

符号一览

符号	描述
Φ Φ	谓词集， Φ=p1,p2,...,pm Φ=p1,p2,...,pm
T(pi) T(pi)	由谓词 pi pi构成的元组集合， T(pi)={(s,o)mid(s,pi,o)inK,piintheta} T(pi)={(s,o)mid(s,pi,o)inK,piintheta}
SIM(pi,p′j) SIM(pi,pj′)	谓词相似度（Predicate Similarity）
P P	匹配谓词对集合（The set of matching predicate pairs）
Pi Pi	匹配谓词对集合的第i个partition，不同的 mathbbPi mathbbPi之间不相交，且并集是 mathbbP mathbbP
Pi Pi	mathbbPi mathbbPi包含的实体集， Pi={(s,s′)mid(s,pi,o)inK,(s′,p′j,o′)inK′,(pi,p′j)inmathbbP} Pi={(s,s′)mid(s,pi,o)inK,(s′,pj′,o′)inK′,(pi,pj′)inmathbbP}
ppk ppk	匹配谓词对（论文中对前后出现的 ppk ppk的定义略有不同，以后文出现的定义为准： ppk=(pi,p′j) ppk=(pi,pj′)，表示某个partition中的第k个匹配谓词对）
S(ppk) S(ppk)	谓词 pi pi对应的实体集， S(ppk)={smids,pi,o} S(ppk)={smids,pi,o}
S′(ppk) S′(ppk)	谓词 p′j pj′对应的实体集， S′(ppk)={s′mids′,p′j,o′} S′(ppk)={s′mids′,pj′,o′}
ρ(ppi,ppj) ρ(ppi,ppj)	匹配谓词对的相似度（Similarity of Matching Predicate Pairs）
W W	谓词对相似度矩阵（Entity Partition阶段会用到）

动机

实体划分的目的是将大规模知识库切成多个划分（patition），从而减少匹配空间，降低计算复杂度。如果直接对实体开刀来做这个划分的工作，势必绕不开巨大的计算量和时间开销。已有的自动对齐算法（automatic alignment algorithms），利用class hierarchy来分割KB。但本文的切入角度更新颖。

我们有如下发现：
（1）相似的实体拥有相同的谓词，比如人都有“出生地”和“出生日期”；
（2）相同的谓词意味着对应的实体是相似的，例如拥有谓词“出生地”的实体可以推断为“人”；
（3）一个知识库中可能有很多实体，但谓词的数量一定不会太多。

基于以上3点，可以巧妙地借助“谓词”对2个知识库中的实体对（entity pair）进行划分，得到多个partition。具体而言，是通过将相似度比较高的谓词对（涉及 谓词对相似度 计算）划分在同一个块内，进而反推出实体对的分块结果。后续的实体对齐，都只在每个partition中单独、并行地进行，达到降低复杂度的作用。

为了计算 谓词对相似度 ，先给出 谓词相似度 的计算方法。

谓词相似度

谓词 pi pi和 p′j pj′分别来自知识库 K K和 K′ K′，相似度计算如下：

begin{align}
SIM(p_i,p'_j)=frac{|T(p_i) bigcap T'(p'_j)|}{|T(p_i) bigcup T'(p'_j)|}
end{align}

当 (s,pi,o) (s,pi,o)和 (s,p′j,o) (s,pj′,o)分别是知识库 K K和 K′ K′的三元组时，我们有 (s,o)inT(pi)bigcapT′(p′j) (s,o)inT(pi)bigcapT′(pj′).  |centerdot| |centerdot|表示集合大小， T(pi) T(pi)的定义参见上文的符号表。

有了谓词相似度的计算方法，对于 K K中的每个谓词 pi pi，都可找到 K′ K′中与之最相似的那个谓词 p′j pj′，称 ppk=(pi,p′j) ppk=(pi,pj′)为匹配谓词对。

对于每个匹配谓词对，都对应有两个实体集：与谓词 pi pi相关的 S(ppk)={smids,pi,o} S(ppk)={smids,pi,o}和与 p′j pj′相关的 S′(ppk){s′mids′,p′j,o′} S′(ppk){s′mids′,pj′,o′}。这俩东东将会用于下面谓词对相似度的计算。

谓词对相似度

begin{align}
rho(pp^i,pp_j)=frac{cos(S(pp^i), S(pp^j)) + cos(S'(pp^i), S'(pp^j))}{2}
end{align}
其中，cos表示两个集合的余弦距离。

接下来，通过改进的HAC聚类算法，即可得到谓词对的划分。Naive的HAC算法复杂度是 O(n3) O(n3)，非常低效。为了加速算法收敛，本工作对每一轮谓词对的合并设定了阈值间隔0.1，使得迭代次数成为常数，将算法复杂度降低到了 O(n2) O(n2).

最后，由谓词对的划分，将谓词对应的实体列出来，即可得到实体对的划分，完成Entity Patition过程。

一个例子

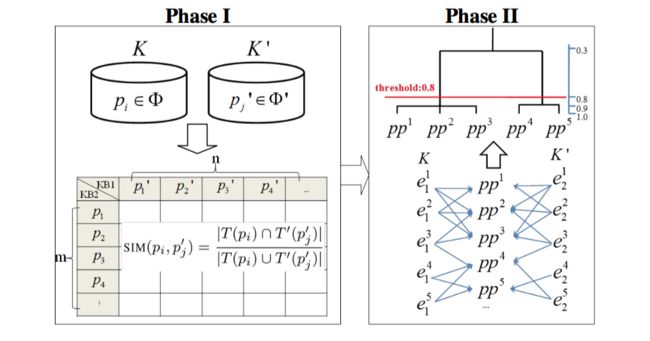
【纠正下：上图Phase I中的 KB1 KB1和 KB2 KB2，作者给写反了】

假设经过Phase I，得到5个谓词对， pp1simpp5 pp1simpp5，且实体和谓词的对应关系如图中Phase II所示。计算得到谓词对相似度如下： rho(pp1,pp2)=0.82 rho(pp1,pp2)=0.82， rho(pp2,pp3)=1 rho(pp2,pp3)=1， rho(pp4,pp5)=0.82 rho(pp4,pp5)=0.82， rho(pp2,pp4)=0.33 rho(pp2,pp4)=0.33， rho(pp2,pp5)=0 rho(pp2,pp5)=0. 给定阈值0.8，并执行改进的HAC聚类算法，可得到2个谓词对集合 {pp1,pp2,pp3} {pp1,pp2,pp3}和 {pp4,pp5} {pp4,pp5}。根据谓词与实体的对应关系，便可得到最终实体对的划分结果： {(ei1,ej2)|i,j=1,2,3} {(e1i,e2j)|i,j=1,2,3}和 {(ei1,ej2)|i,j=3,4,5} {(e1i,e2j)|i,j=3,4,5}.

Partial Order Construction

快读

将知识库分块后，并行地在每个块内构件偏序集，目的是使得“通过已知问题推断未知问题的答案”成为可能，这样做可进一步降低开销。作者基于实体对之间的相似度关系给出偏序定义。当我们能对每个实体对计算出谓词相似度和总相似度后，偏序关系即可建立。

读后感受：作者对这部分的工作做得非常细致，不仅体现在对权重计算的精准追求上，也体现在对复杂度的极致优化上。

符号一览

符号	描述
pij pij	实体对 (ei,ej) (ei,ej)， (ei,ej)inP (ei,ej)inP
skij sijk	pij pij在匹配谓词对 ppk ppk上的相似度
sij sij	pij pij在某个partition中所有匹配谓词对上的相似度
qf(pi) qf(pi)	pi pi的Functionality
ωk ωk	谓词 pk pk的权重（不同的谓词有不同的重要性）
θ θ	sij sij的阈值，用于控制matching scale

动机

构建偏序集的目的是：仅通过少量已知问题的答案，就可以推断出那些未知问题的答案。这里跟半监督学习中样本提纯阶段的思想有点儿像。

在每个partition中并行地构建偏序集。偏序定义如下：

给定2个实体对 pij=(ei,ej) pij=(ei,ej),  pi′j′=(ei′,ej′) pi′j′=(ei′,ej′)，当满足 skijgeqski′j′ sijkgeqsi′j′k且 sumk(skij)>sumk(ski′j′) sumk(sijk)>sumk(si′j′k)，有 pijsuccpi′j′ pijsuccpi′j′，我们说 pij pij和 pi′j′ pi′j′是可比较的，且 pij pij precedes  pi′j′ pi′j′（ pij pij在 pi′j′ pi′j′之前/之上） 或 pi′j′ pi′j′ succeeds  pij pij（ pi′j′ pi′j′在 pij pij之后/之下）。

由此可见，只要计算出实体对在各个匹配谓词对 ppk ppk上的相似度 skij sijk，以及实体对相似度（The total entity pair similarity） sij sij，即可轻松构建出偏序集。

实体对相似度计算

话虽这样讲， sij sij却不是那么容易计算的。我们且看作者是如何处理的：
前文提到过，谓词可以是关系或属性，因此计算 skij sijk时，根据谓词的类型形成“关系对”或“属性对”，进一步构建“关系向量对”或“属性向量对”，以两个向量的余弦相似度作为 skij sijk。

当然，我们完全可以在得出 skij sijk后，简单粗暴取个平均值即作为 sij sij的值。但是要想拿到Best Paper奖，这么做必然是差了点儿意思。

作者认为，不同的谓词，其重要性不同，因此有必要赋予不同的权重。为了表达谓词的权重，定义2个概念：

• Functionality： qf(pi) qf(pi)，很容易计算：
  begin{align}

qf(p_i)=frac{|\{s|exists o:(s,p_i,o) in K\}|}{|\{ |(s,p_i,o) in K\}|}
end{align}

• Inverse Functionality： qf−1(pi)=qf(p−1i) qf−1(pi)=qf(pi−1)，其中 p−1i pi−1是 pi pi是倒置，e.g., 如果有 (s,pi,o) (s,pi,o)，那么有 (o,p−1i,s) (o,pi−1,s).

谓词权重基于Inverse Functionality来计算：

begin{align}
s_{ij}=sum_{k=1}^m omega_k centerdot s^k_{ij}
end{align}
其中，
begin{align}
omega_k=frac{qf^{-1}(p_k)}{sum_{t=1}^m qf^{-1}(p_t)}
end{align}

理论上，有了上述计算结果，根据偏序的定义即可得到偏序集。但这中间存在计算复杂度的问题：如果一个partition中来自 K K和 K′ K′的实体数量依然较多，通过笛卡尔积操作将会组合得到非常多的实体对，使得上述的计算开销依然不小。

为了解决这个问题，作者先后采取了2个手段：通过倒排索引（inverted index）和前缀过滤器（prefix filter）技术prune匹配空间，然后再计算 sij sij；随后，设定阈值 theta theta进一步过滤实体对。最终，构建偏序集的算法复杂度由 mathcalO(n2) mathcalO(n2)降低到 mathcalnlogm−1n+|varepsilon| mathcalnlogm−1n+|varepsilon|， m m是匹配谓词对的数量， |varepsilon| |varepsilon|是实体对构成的偏序数量。

一个例子

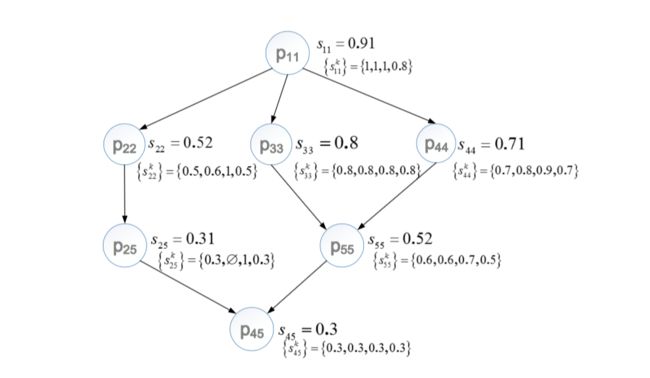
假设某个partition中有4个谓词对，谓词权重分别是0.439, 0.0486, 0.0244, 0.488；假设来自知识库 K K和 K‘ K‘各有5个实体，此时通过笛卡尔积操作将得到25个实体对，进一步假设通过阈值过滤后，剩下7个实体对。按上文所述方法，分别计算得到每个实体对的 skij sijk和 sij sij。最后根据偏序的定义，即可得到偏序关系如下图所示。

Question Selection

快读

偏序集构建完毕后，眼下的任务是从中选取一些问题，分发给众包参与者，获取答案后对偏序集中的其他未知问题进行推理。不同的问题（或者说实体对）具有不同的推断能力，我们的原则是挑选哪些推断能力比较强的问题入选问题集，并分发给众包参与者来获取答案。为了衡量某个实体对（或者说某个问题）的推断能力，作者提出了推断期望的概念，并分别给出了 实体对推断期望 和 问题集推断期望 的计算方法。作者证明了Question Selection是NP-hard的，并给出了2个启发式的算法来解决。

读后感受：衡量实体对的推断能力是个不太容易的事情，作者提出了推断期望的概念，并巧妙地通过一个假设，让推断期望的计算成为可能。行文至此，作者依然不断地定义问题、证明问题NP-hard、给出算法解决问题并分析复杂度，在内容饱满度方面依然感人。不过进入到这里后，论文中的小瑕疵开始变多，有些重要的地方缺少表述，还有不少typo. 精读过程中若有任何疑问，期待与你交流！

符号一览

符号	描述
B B	预算
pre(pij) pre(pij)	偏序关系中，位于 pij pij上方（或前面）的实体对
suc(pij) suc(pij)	偏序关系中，位于 pij pij下方（或后面）的实体对
E(pij) E(pij)	实体对 pij pij的推断期望（Inference Expectation）
Q Q	问题集
ΔE(Q) ΔE(Q)	pij pij带来的推断期望增益， DeltaE(Q)=E(Qbigcup{pij})−E(Q) DeltaE(Q)=E(Qbigcup{pij})−E(Q)

Inference Model

推断模型是降低开销的举措，目的是在只知道少量问题的答案的情况下，即可根据偏序关系推断出其他问题的答案。不然的话只能人工一个个去标记，耗钱、耗时又耗力。

给定偏序集，如果实体对 pi pi是匹配的，那些位于 pi pi之前的所有实体对都可以初步推断为是匹配的（至于为何表述为“初步匹配”，在下文的Error Tolerance中可见分晓），因为它们的实体相似度比 pi pi的实体相似度更大；同理，如果实体对 pi pi不匹配，那些位于 pi pi之后的所有实体对都可以初步推断为不匹配。这里是给出了定性的描述，下文在定义推断期望时，会有定量的分析。

作者定义Question Selection如下：

给定偏序集，在给定的预算下，选择 B B个问题（用于向众包参与者寻求答案），使得可推断出的实体对数量最大化。
注意： mathcalB mathcalB本来是为众包机制给定的预算，这里相当于假设每个问题的预算是1，那么预算 mathcalB mathcalB就对应 mathcalB mathcalB个问题喽。

此外，根据每个问题的推断能力是否提前已知，作者又分别定义了Offline Problem（已知）和Online Problem（未知）。对于Offline Problem，作者给出了NP-hard证明。同时，Online Problem与之相比更难，因此也是NP-hard的。

下面看看作者是如何计算单个实体对的推断期望和实体对组成的问题集的推断期望的。

单个实体对的推断期望

begin{align}
E(p_{ij})=s_{ij} centerdot |pre(p_{ij})| + (1-s_{ij}) centerdot |suc(p_{ij})|
end{align}

pre(pij) pre(pij)表示位于 pij pij之前/之上的实体对， suc(pij) suc(pij)表示位于 pij pij之后/之下的实体对。实体对 pij pij匹配的概率是 sij sij，意味着位于 pij pij之前/之上的实体对有 sij sij的概率可以被推断；同时，实体对 pij pij不匹配的概率是 1−sij 1−sij，意味着位于 pij pij之后/之下的实体对有 1−sij 1−sij的概率被推断。基于此，我们有了上述计算实体对推断期望的公式。

问题集 Q Q的推断期望

问题集的推荐期望是指：当我们知道问题集中所有问题的答案时，实体对 p′ij pij′能被推断的概率， E(p′ij|Q) E(pij′|Q)。

当计算得到所有实体对的推断期望后，我们可能自然而然想到：直接把构成问题集的每个实体对的推断期望相加，即是问题集的推断期望。遗憾的是这个问题并没这么简单，因为在问题集中，一个实体对可能有不止一个preceding/succeeding，导致推断期望之间存在overlap.

为了使得问题集的推断期望可计算，我们做出如下假设：
问题集Q中的所有实体对之间，不存在preceding/succeeding关系。

显然，事实上这个假设不成立，因为一定是存在这样的关系。但是通过一些转化，可以让假设成立：如果2个实体对存在前后/上下关系，we can remove one of them as one can be inferred by another.

下面给出不同CASE下 E(p′ij|Q) E(pij′|Q)的计算方法。

三种CASE

Case 1:  p′ij pij′ 在问题集 Q Q之前/之上
记问题集 Q Q中，位于 p′ij pij′之后的问题子集是 QP QP，那么 p′ij pij′可以被推断的概率是：

begin{align}
E(p'_{ij}|Q)=E(p'_{ij}|Q^P)=1-Pi_{p_{ij} in Q^P}(1-s_{ij})
end{align}

其中， sij sij表示问题集 QP QP中每个实体对 pij pij的相似度。它被 QP QP推理出的概率等于它不被 QP QP中任何一个question所推理出的概率（即 PipijinQP(1−sij PipijinQP(1−sij）的complementary event（即 1−PipijinQP(1−sij) 1−PipijinQP(1−sij)）

Case 2:  p′ij pij′ 在问题集 Q Q之后/之下
记问题集 Q Q中，位于 p′ij pij′之前的问题子集是 QW QW，那么 p′ij pij′可以被推断的概率是：

begin{align}
E(p'_{ij}|Q)=E(p'_{ij}|Q^W)=1-Pi_{p_{ij} in Q^W}(s_{ij})
end{align}

Case 3:  p′ij pij′ 无法由问题集 Q Q推断
意味着 p′ij pij′是个孤立点，与问题集Q中的任何问题都没有形成偏序关系。此时有：

begin{align}
E(p′ij|Q)=0 E(pij′|Q)=0
end{align}

至此，我们可以计算出问题集的推断期望：

begin{align}
E(Q)=sum_{p'_{ij}}E(p'_{ij}|Q)
end{align}

有个 E(Q) E(Q)，就可以进行问题选择了。作者提出了2个算法来解决这个NP-hard问题。

Two Greedy Algorithms

基于推断模型和前文提出的Offline Problem，作者分别提出了串行的SQS和并行的MQS算法，在给定的预算 B B下，选出推断能力最好的那些问题。

SQS算法的思路很简单（见下图），复杂度也很低（ O(Bn) O(Bn)），但是没法实际落地，因为每选出一个问题，就要分发到众包平台等待答案，然后才能开始下一次迭代。。。
思路简述如下：

1. 计算得到每个实体对的推荐期望
2. 选择推断期望最高的问题加入问题集 Q Q，并分发到众包平台获取答案
3. 根据答案是YES或NO，将偏序图上位于选中问题之前（答案是YES时）或之后（答案是NO时）的所有实体对节点去除，并重新计算图中剩余实体对的推断期望
4. 继续从步骤2开始，直到给定的预算消耗完毕（或找到指定数量的问题）
   

MQS算法（见下图）稍微麻烦一点，思想上有点类似于随机森林选特征的过程：根据“ pij pij对问题集的推断期望的增益”来选择问题。
不过对于该算法我有一处疑问：第一轮迭代结束后， δ δ的值倘若比较大，会导致在后续的迭代中第9行和第12行的条件均不能得到满足，岂不是只能选到一个问题就结束了？（有看懂的小伙伴欢迎留言探讨。针对该疑问，我也会在论文作者答复后进行更新。）

一个例子

偏序关系如上图所示，假设预算 B=2 B=2。
对于SQS算法：

1. 计算得到每个实体对的推荐期望；根据前文计算单个实体对推断期望的公式，以 E(p55) E(p55)和 E(p22) E(p22)为例， E(p55)=0.52times3+0.48times1=2.04 E(p55)=0.52times3+0.48times1=2.04， E(p22)=0.52times1+0.48times2=1.48 E(p22)=0.52times1+0.48times2=1.48，其他结果见下图SQS的Iteration 1那一行
2. 选择推断期望最高的问题 p55 p55加入问题集 Q Q，并分发到众包平台获取答案
3. 假设答案是YES，去掉 p11 p11,  p33 p33,  p44 p44。图中剩余 p22 p22,  p25