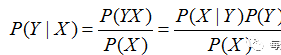数据挖掘十大算法（九）：朴素贝叶斯 python和sklearn实现

第三个算法终于算是稍有了解了，其实当你结合数据了解了它的实现原理后，你会发现确实很朴素。这里对朴素贝叶斯算法做一个介绍和总结，包括（原理、一个代码示例、sklearn实现），皆为亲自实践后的感悟，下面进入正文。

原理：

首先我们需要了解概率论的一些简单知识：

最后推导出的就是贝叶斯公式，这里说一下我的感悟：上面的公式如果就这样不结合数据来看，是很容易理解的，我用了几分钟便了解了这个高中学过的东西。但是在我将它和实际数据之间联系起来时，却花了几个小时。毕竟得到一个公式只是基础，如果不能在数据上运用得当那也是无用武之地。下面就这个问题说一下：

朴素贝叶斯的原理：根据一些先验概率计算Y变量属于某个类别的后验概率

    先验概率：是指现有数据根据以往的经验和分析得到的概率

    后验概率：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小

    一个通俗的理解：你求出了你在百思图买了一双白鞋的概率，那么如何得知你买了一双白鞋而这双白鞋就在百思图的概率呢。

 

这就是利用先验概率来求得后验概率的问题，再拿一个数据说明（引入他人的）：

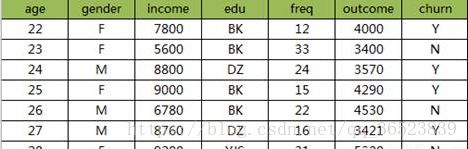
上表中的信息反映的是某P2P企业判断其客户是否会流失(churn)，而影响到该变量的因素包含年龄、性别、收入、教育水平、消费频次、支持。那根据这样一个信息，我该如何理解朴素贝叶斯的思想呢？再来看一下朴素贝叶斯公式：

从公式中可知，如果要计算X条件下Y发生的概率，只需要计算出后面等式的三个部分，X事件的概率（P(X)），是X的先验概率、Y属于某类的概率（P(Y)），是Y的先验概率、以及已知Y的某个分类下，事件X的概率（P(X|Y)），是后验概率。从上表中，是可以计算这三种概率值的。即：

P(X)指在所有客户集中，某位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率；

P(Y)指流失与不流失在所有客户集中的比例（4:3）；

P(X|Y)指在已知流失的情况下，一位22岁的本科女性客户，其月收入为7800元，在12次消费中合计支出4000元的概率。

如果需要选出某样本属于哪类，则需要根据该条样本求出它属于每个类的概率，选择最大概率的那个类。

由于是比较概率，而非求出值，所以P(X)是可以忽略的，同时P(Y)很容易求出，所以P(X|Y)越大，那么P(Y|X)就越大。但是单上面的数据我们是不可能求出P(X|Y)概率，因为X代表的是许多的特征而每个特征之间有着一定的关系（如 收入：消费频率 正相关），而引入朴素贝叶斯理论则可以求了。

朴素贝叶斯之所以朴素是因为它默认X的每个特征都是独立的，回归原始。故而P(X|Y)的概率就可以计算为：

即求出每个特征的概率，再相乘便可以求出P(X|Y)的概率。（这里提个醒概率值较小，相乘后出现下溢出四舍五入可能为0，所以可以引入ln来计算每个特征概率，由于ln(a*b) = ln(a)+ln(b)所以可以避免这个问题）那么如何求出X各个特征的概率呢？下面我引入一个个机器学习实战的例子：

示例：过滤网站恶意留言

一个很简单的例子，我本来想使用DataFrame来重新实现，但是这样可能比原来还复杂了，所以引用了原来的numpy结构来处理。

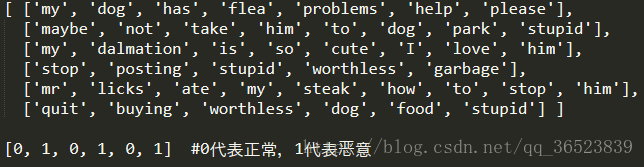
说明：有一堆已经清理好的留言单词及它的所属类，现在根据已有的数据求一条新的留言所属分类。

样本数据如上：六条已经划分好了的留言数据集，以及各自对应的分类。具体看下面的代码及注释：

from numpy import *

#加载数据
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]
    return postingList, classVec

#合并所有单词，利用set来去重，得到所有单词的唯一列表
def createVocabList(dataSet):
    vocabSet = set([])
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

#优化词集模型= 为 词袋模型+=，将单词列表变为数字向量列表
def bagOfWords2VecMN(vocabList, inputSet):
    returnVec = [0] * len(vocabList)    #获得所有单词等长的0列表
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1   #对应单词位置加1
    return returnVec

# 返回的是0、1各自两个分类中每个单词数量除以该分类单词总量再取对数ln 以及0、1两类的比例
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 样本数
    numWords = len(trainMatrix[0])  # 特征数
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # 1类所占比例
    p0Num = ones(numWords)
    p1Num = ones(numWords)  #初始化所有单词为1
    p0Denom = 2.0
    p1Denom = 2.0  #初始化总单词为2        后面解释为什么这四个不初始化为0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:       #求1类
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]     #求0类
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num / p1Denom)  # numpy数组 / float = 1中每个单词/1中总单词
    p0Vect = log(p0Num / p0Denom)  # 这里为什么还用ln来处理，后面说明
    return p0Vect, p1Vect, pAbusive

#P(X|C)判断各类别的概率大小（这里是0、1）
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)  # 相乘后得到哪些单词存在，再求和，再+log(P(C))
    p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1) # 由于使用的是ln，这里其实都是对数相加
    if p1 > p0:
        return 1
    else:
        return 0

#封装调用的函数
def testingNB():
    listOPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(bagOfWords2VecMN(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses))
    #上面求出了0、1两个类中各单词所占该类的比例，以及0、1的比例

    #下面是预测两条样本数据的类别
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = array(bagOfWords2VecMN(myVocabList, testEntry)) #先将测试数据转为numpy的词袋模型 [0 2 0 5 1 0 0 3 ...]
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb)) #传值判断

    testEntry = ['stupid', 'garbage']
    thisDoc = array(bagOfWords2VecMN(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))

if __name__=="__main__":
    testingNB()

从多个例子中选了这个最简单，但思路完整的例子。以上只有0、1两个类，如果有多个类别，个人觉得则可以使用字典来保存各类的比例。如果需要分类许多邮件等，预先获得它们的分类，使用正则匹配、清洗获取每个单词，将每封邮件转为上述示例中的一条列表，最后做相同的处理。这便是一个样例扩展。

这里重点说明代码中的两点，千万留心：

    1：我们初始化单词列表和总单词数时，初始化为1和2，并不是0，这是因为——利用贝叶斯分类器对文档进行分类时，要计算多个概率的乘积以获得文档属于某个类别的概率，即计算p(w0|c)p(w1|c)p(w2|c)。如果其中一个特征概率值为0，那么最后的乘积也为0.为降低这种影响，可以将所有词出现数初始化为1，并将分母初始化为2。

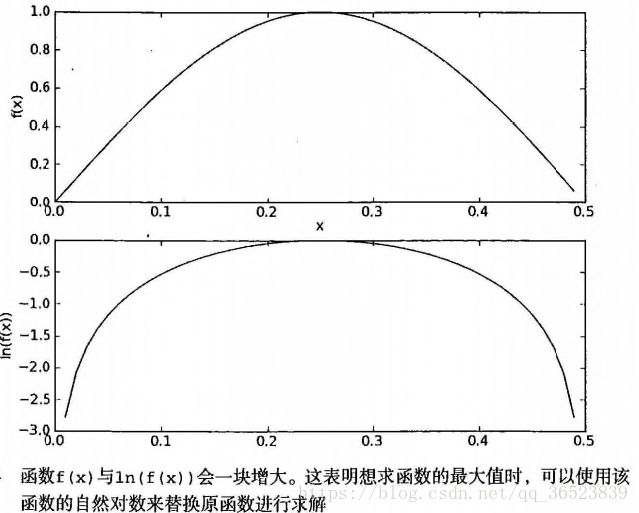
    2：另一个问题是下溢出，由于太多小数相乘造成的。当计算乘积p(w0|c)p(w1|c)p(w2|c...p(wn|c)时，由于大部分因子都很小，所以程序会下溢出得不到正确的答案。（多个相乘，python四舍五入得到0）一种解决办法是对乘积取自然对数。代数中的这个公式可以解决我们的问题：ln(a*b) = ln(a) + ln(b)，对数处理后将乘转化为加，来避免下溢出问题。同时，采用自然对数不会有任何损失。引用一张图：

当然第二个问题我是想不到的，这是作者的思想，个人觉得很不错，所以采用了。

 

----------------------------------------------------------------------------------------------------------------------------------------

下面将使用sklearn来实现朴素贝叶斯算法。

sklearn实现：

在sklearn中实现了三类朴素贝叶斯：GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)

所以由于需要介绍的内容太多，所以这里给一篇文章介绍sklearn的朴素贝叶斯，翻译自官方文档，本人转载了，如果需要请参考《sklearn——朴素贝叶斯》

 

本文有部分资料参考下面的文章，在此感谢

参考文章：https://www.zhihu.com/question/19960417

参考文章：https://www.cnblogs.com/yemanxiaozu/p/7680761.html

参考文章：https://blog.csdn.net/ten_sory/article/details/81237169

《机器学习实战》