2.3 浮点数的表示与运算

浮点数表示法是指以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。所以，在位数有限的情况下，既扩大了数的表示范围，又保持了数的有效精度。

浮点数表示为 （可以想象下科学计数法）

r是浮点数阶码的底（隐含），与尾数的基数相同，通常r=2。E和M都是有符号的定点数，E称为阶码，M称为尾数。

阶码是整数，阶符Jf和阶码的位数m共同反映浮点数的表示范围及小数点的实际位置；数符Sf代表浮点数的符号；尾数的位数n反映浮点数的精度。

规格化浮点数，为了提高运算的精度，需要充分地利用尾数的有效数位，通常采用浮点数规格化形式，即规定尾数的最高数位必须是一个有效值。

左规：当浮点数运算的结果为非规格化时要进行规格化处理，将尾数算数左移一位，阶码减1（基数为2时）的方法称为左规，左规可能要进行多次。

右规：当浮点数运算的结果尾数出现溢出，将尾数算术右移一位，阶码加1（基数为2时）的方法称为右规。当需要右规时，只需要进行一次。

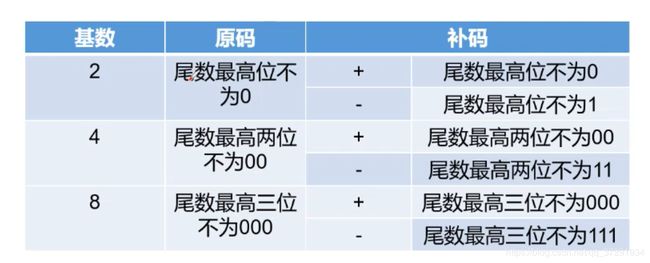
下面是基数不同时候的规格化标准

IEEE754标准

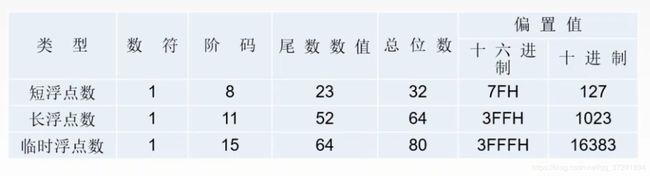
IEEE754标准规定常用的浮点数格式有短浮点数（单精度，float型） ,长浮点数（双精度，double型），临时浮点数

短浮点数与长浮点数都采用隐含尾数最高数位的方法，故可多表示一位尾数。临时浮点数又称扩展精度浮点数，无隐含位。

阶码以移码存储，尾码以原码存储。

 规格化的短浮点数的真值为 

其中，s=0表示正数，s=1表示负数；短浮点数E的取值1~254（8位表示），M为23位，共32位。（偏执值为127而非128，空出8位全1来表示无穷大，阶码值E的范围为1~254，空出全0表示非规格化数）

浮点数的加减运算

浮点数运算时阶码运算和尾数运算分开进行。浮点数的加减法采用补码。

1> 对阶 

对阶的目的是使两个操作数的小数点位置对齐，即使得两个数的阶码相等。为此，先求阶差，然后小阶向大阶看齐的原则，将阶码小的尾数右移一位（基数为2）,阶码加1，直到两个数的阶码相等为止。

2> 尾数求和

将对阶后的尾数按定点数加（减）运算规则运算。

3> 规格化

以双符号为例，当尾数的最高数值位与符号位不同时，即为规格化形式。规格化分为左规与右规。

左规：当尾数出现00.0xxx..x或11.1xxx...x时，需左规，即尾数左移1位，和的阶码减1，直到尾数为00.1xxx...x或11.0xxx...x

右规：当尾数求和结果溢出，需要右规，即尾数右移一位，和的阶码加1。

4> 舍入

在对阶和右规的过程中，可能会将尾数低位丢失，引起误差，影响精度。常见的舍入方法有：“0”舍“1”入法和恒置“1”法。

“0”舍“1”入法：类似于十进制数运算中的“四舍五入”法，即在尾数右移时，被移去的最高数值位为0，则舍去；被移去的最高数值位为1，则在尾数的末位加1。这样做可能会使尾数又溢出，此时需再做一次右规。

恒置“1”法：尾数右移时，无论丢掉的最高数值位是“1”还是“0”，都使右移后的尾数末位恒置为“1”。这种方法同样有使尾数变大和变小两种可能。

5> 溢出判断

尾数之和（差）出现01.xxx或10.xxxx时，并不表示溢出，只能将此数右规后，再根据阶码来判断浮点数运算结果是否溢出。

浮点数的溢出与否是由阶码的符号决定的。比如双符号位“01”，“10”表示上溢和下溢。所以阶码符号位不同表示溢出。