机器学习与评分卡
机器学习简介
什么是机器学习
- 如果一个系统能够通过执行某个过程改变它的性能,这就是学习(什么是学习)
- 不用编程去指定机器做什么,而是让机器有能力自己学习
- 首先定义任务T,经验E,表现P,如果机器有一个任务T,随着经验E的增多,表现P也会变好,则表示机器正在经验E中学习
三要素
- 模型(机器学习的成果,条件概率分布或决策函数)
- 策略(计算模型的方式)
- 算法
生活中的机器学习应用
- 垃圾邮件分类
- AlphaGo围棋AI
- 医疗行业
- 人声识别
监督学习
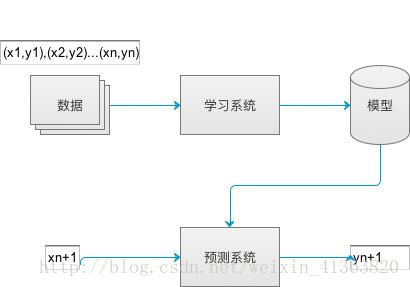
学习一个模型,使模型对给定输入做出相应的预测输出,流程如下图
其中自变量x为自变量,是实例的特征向量;y为因变量,是实例的结果。
监督学习主要解决分类与回归两类问题
监督学习实例
已知房价,平米数的训练集如下:
| 平米数 | 房价(万) |
|---|---|
| 50 | 50 |
| 80 | 70 |
| 100 | 90 |
| 130 | 110 |
| 150 | ??? |
给定一个平米数,预测该面积房价。
无监督学习
从数据中自主学习,分析数据的类别结构
评分卡介绍
什么是评分卡(信贷场景中)
- 以分数的形式来衡量风险几率的一种手段
- 对未来一段时间内违约/逾期/失联概率的预测
- 通常评分越高越安全
- 根据使用场景分为反欺诈评分卡、申请评分卡、行为评分卡、催收评分卡
为什么要开发评分卡
- 风险控制的一个环节,根据已有数据提供逾期概率指标参考
评分卡的特性
- 稳定性
- 预测能力
- 等价于逾期概率
评分卡开发的常用模型
- 逻辑回归
- 决策树
- 组合模型
基于逻辑回归的评分卡理论依据
一个事件发生的几率(Odds),是指该事件发生的概率与该事件不发生概率的比值。若一个客户违约概率为p,则其正常的概率为1-p,由此可得:
Odds=p1−pOdds=p1−p
此时,客户违约的概率p可以表示为:
p=Odds1+Oddsp=Odds1+Odds
评分卡表达式为:
Score=A−Blog(Odds)Score=A−Blog(Odds)
其中A、B为常数。由于log函数在(0→+∞)(0→+∞)单调递增,所以当用户违约几率Odds越大时,Score评分越低。
通过给定
(1)某特定Odds时的Score值S0S0;
(2)该特定Odds值翻倍时Score增加值PD0PD0;
通过给定值S0S0与PD0PD0带入评分卡表达式,可求得A、B。
通过以上分析,求该用户评分Score的问题则转化为求用户违约对数几率log(Odds)log(Odds)的问题。
依照二元逻辑回归构造预测函数
hθ(x)=g(θTx)=11+e−θTxhθ(x)=g(θTx)=11+e−θTx
其中hθ(x)hθ(x)表示结果取1的概率。
推倒可得该事件的对数几率log(Odds)log(Odds)如下:
log(Odds)=logp1−p=loghθ(x)1−hθ(x)=log11+e−θTx1−11+e−θTx=θTxlog(Odds)=logp1−p=loghθ(x)1−hθ(x)=log11+e−θTx1−11+e−θTx=θTx
可以发现:在逻辑斯蒂回归模型中,输出Y=1的对数几率是输入条件x的线性函数。
θTx=∑i=1nθixi=θ0+θ1x1+θ2x2+...+θnxnθ=⎡⎣⎢⎢⎢θ0θ1...θn⎤⎦⎥⎥⎥,x=⎡⎣⎢⎢⎢x0x1...xn⎤⎦⎥⎥⎥θTx=∑i=1nθixi=θ0+θ1x1+θ2x2+...+θnxnθ=[θ0θ1...θn],x=[x0x1...xn]
由此可得log(Odds)=θ0+θ1x1+...+θnxnlog(Odds)=θ0+θ1x1+...+θnxn
回到信贷业务中
目标:寻找最理想的参数估计θθ使得模型预测的概率相对已有样本最准确。
方法:损失函数最小化求得θθ
逻辑回归的损失函数为对数损失函数(具体可由极大似然估计推倒):
L(θ) =1m∑i=1mCost(hθ(x(i)),y(i))=−1m[∑i=1m(y(i)⋅log(hθ(x(i)))+(1−y(i))⋅log(1−hθ(x(i)))]L(θ)=1m∑i=1mCost(hθ(x(i)),y(i)) =−1m[∑i=1m(y(i)⋅log(hθ(x(i)))+(1−y(i))⋅log(1−hθ(x(i)))]
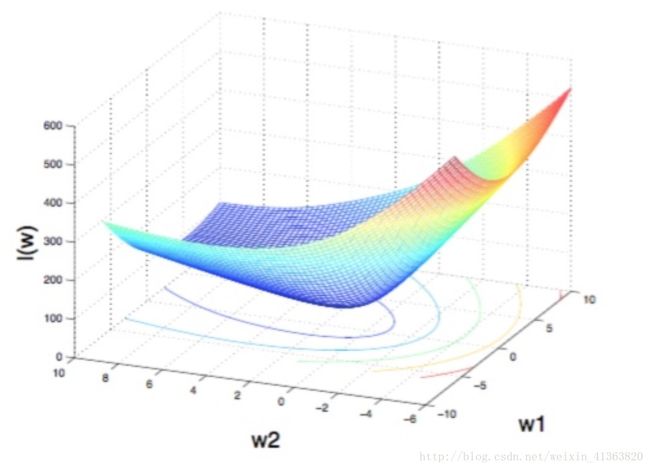
利用梯度下降法求得minL(θ)minL(θ),得到θθ
Repeat {
θj:=θj−α∂∂θj∑i=1m(hθ(x(i))−y(i))x(i)jθj:=θj−α∂∂θj∑i=1m(hθ(x(i))−y(i))xj(i)
}(同时更新所有θjθj)
数据处理流程
数据可视化
可以通过数据可视化来验证我们对数据分布的一些猜想,使我们对数据分布有一个清晰的认识和理解,并且由此设计一些合理的人工规则。
方式:
- 各种图形展现工具
用途:
- 理解数据
- 方便数据探索
- 辨别分析离群点
数据清洗
1.检验异常样本
根据对具体业务的理解和认识去除一些异常极端的数据。例如在对网页浏览量的分析,可能需要去除爬虫用户的浏览数据。
2.缺省字段的处理
数据样本的某些特征字段可能有缺省值,需根据缺省值多少与特征类型区分处理
- 缺省值很多时直接舍弃。作为特征加入的话,可能反倒带入噪声,影响最后的结果。
- 非连续特征缺省量适中时,将Nan作为一个新类别加入至特征中
- 连续特征缺省量适中时,考虑给定一个step(比如age,我们可以考虑每隔2/3岁为一个步长),然后把它离散化,之后把NaN作为一个type加到属性类目中
- 缺省值很少时利用填充的办法进行处理。例如用均值、中位数、众数填充,模型填充等
特征分箱
分箱的定义
- 将连续变量离散化
- 将多状态的离散变量合并成少状态
分箱的重要性及其优势
- 离散特征的增加和减少都很容易,易于模型的快速迭代;
- 稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
- 离散化后的特征对异常数据有很强的鲁棒性;
- 离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
- 可以将缺失作为独立的一类带入模型。
WOE(Weight of Evidence)编码
评分卡模型中一般会将特征进行WOE编码。WOE是一种有监督的编码方式,将预测类别的集中度的属性作为编码的数值。
优势
- 将特征的值规范到相近的尺度上。 (经验上讲,WOE的绝对值波动范围在0.1~3之间)。
- 具有业务含义。(自变量取某个值时对因变量正负比例的一种影响)
缺点
- 每个箱都包含好坏两个类别,计算成本增加
WOE计算公式
WOE=log(Gi/GtotalBi/Btotal)WOE=log(Gi/GtotalBi/Btotal)
其中Gi,BiGi,Bi分别为自变量第i箱好样本个数与坏样本个数
求得WOE值取代原特征值做自变量进行训练。
数据采样
在数据正负样本不均衡情况下,当然正负样本不要求1:1,但是也不能太大。假如正负样本比例 1:10,把这样不均衡的数据直接放进模型中进行训练,准确率会很高,因为大部分都可以预测为负样本。但是训练出的模型泛化能力很弱。这时需要对数据进行采样,使得数据样本均衡。通常有四种办法来进行采样。
- 从负样本中抽取部分样本出来和正样本结合
- 正样本重复若干次
- SMOTE(原理及实现)
- 代价敏感学习
评分卡模型训练
算法
- 使用逻辑回归算法进行训练
两类错误
- 将坏人预测为正常借款人
- 将正常人预测为坏人
注意:在借贷业务中以上两种错误带来的代价不用!
应对
- 在目标函数或损失函数中增加逾期权重。
- 较差验证选择合适权