Python中杨辉三角的理解（廖雪峰教程例）

在看到廖雪峰教程生成器一节习题杨辉三角时，一开始感觉很苦恼，没有思路，网上的各种解答也只是梳理程序执行过程，而没有抽象化解决问题的思路

注意：看此教程前请先学习生成器的原理，yield返回的用法规律，不然可能会懵逼。

下面我按照自己的理解写下思路：

首先附上我们需要求得的杨辉三角：

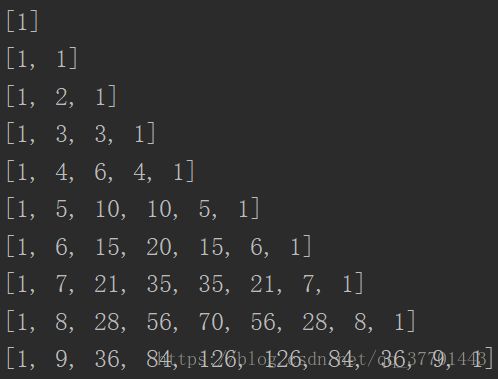
[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

[1, 5, 10, 10, 5, 1]

[1, 6, 15, 20, 15, 6, 1]

[1, 7, 21, 35, 35, 21, 7, 1]

[1, 8, 28, 56, 70, 56, 28, 8, 1]

[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]

很显然，是按照一行一个数列（list）实现的，也就是说，我们得在程序中不断的返回每一行的list并且打印出来

 

第一步：先找规律，抽象化问题：

首先我们观察到，第一行为[1]，我们直接赋给一个变量：初始化数列 p = [1]

其次我们观察到，下面的每一行的开头结尾都是[1],那么我们可以推导出每一行的规律为：[1]+.........+[1]

那么我们发现，从第三行开始中间的 [2]，第四行中间的 [3，3]，第五行中间的 [4,6,4] 等等以此类推才是我们需要推导的部分

第一行：[1] 设 p = [1]

第二行：[1]+[1] 设 p = [1,1]

第三行：[1]+[2]+[1] 设 p = [1,2,1]

第四行：[1]+[3]+[3]+[1]设 p = [1,3,3,1]

....

经过找规律，我们发现，每一个新的list中间的部分，都等于上一行list的：第0个元素+第1个元素，第1个元素+第2个元素，第2个元素+第3个元素,.......

加上头尾也就是[1] +[p[0]+p[1]]+[p[1]+p[2]].....+[1]

比如上面第三行：p[0] = 1, p[1] = 2, p[2] = [1]

那么第四行就是：[1] + [1+2] (# p[0]+p[1])+ [2+1](# p[1]+p[2])+ [1]

后面以此类推

 

既然核心点是这个除去首位两个 [1] 的中间部分：[p[0] + p[1]]+[p[1] + p[2]]+[p[2] + p[3]]........

我们很容易得到规律：[p[i] + p[i+1]]# for i  in range(x)

如果还没看懂，你可以找一张纸，将每一行都按照这个规律写出来：

new p代表本行list的中间部分，p代表上一行list：

 

[1]

[1]+[1]

[1]+[2]+[1] new p = p[0] + p[1] / i = 0,1 需要 i in range(1)

# range(1) = 0,根据[p[i] + p[i+1]]即可实现p[0]+p[0+1]

[1]+[3]+[3]+[1] new p = p[0] + p[1], p[1] + p[2] /i = 0,1,2 需要 i in range(2)

[1]+[4]+[6]+[4]+[1] new p = p[0] + p[1], p[1] + p[2], p[2] + p[3] /i = 0,1,2,3 需要 i in range(3)

[1]+[5]+[10]+[10]+[5]+[1] new p = p[0] + p[1], p[1] + p[2], p[2] + p[3], p[3] + p[4] /i = 0,1,2,3,4需要 i in range(4)

 

 

i的规律为上一行list元素个数-1，也就是len(p) - 1

至此，已经可以得出推导式：

 

[1] + [p[i] + p[i + 1] for i in range(len(p) - 1)] + [1]

 

补全程序代码：

 

def triangles():
    p = [1]
    while True:
        yield p#generator函数与普通函数的差别：在执行过程中，遇到yield就中断，下次又继续执行
        p = [1] + [p[i] + p[i+1] for i in range(len(p)-1)] + [1]
n = 0
for t in triangles():
    print(t)
    n = n + 1
    if n == 10:
        break

结果：