神经网络
神经网络
7.1 什么是人工神经网络
人工神经网络受到生物神经网络的启发。构造人工神经元来模仿生物神经元来工作。
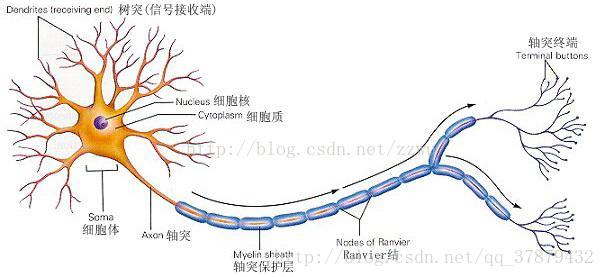
生物神经网络的基本工作原理:一个神经元的输入端有多个树突,主要是用来接收输入信息的。输入信息进过突触处理,将输入的信息累加,当处理后的输入信息大于某一个特定的阈值,就会把信息通过轴突传输出去,这时称神经元被激活。相反,当处理后的输入信息小于阈值时,神经元就处于抑制状态,它不会像其他神经元传递信息。或者传递很小的信息。
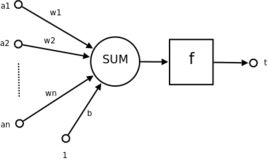
上图是人工神经网络的模型。sum :加权 f:激活函数
人工神经网络分为两个阶段:
1 :接收来自其他m个神经元传递过来的信号,这些输入信号通过与相应的权重进行加权求和传递给下个阶段。(预激活阶段)
2:把预激活的加权结果传递激活函数
生物神经网络 人工神经网络
细胞核 神经元
树突 输入
轴突 输出
突触 权重
【突触使神经细胞的膜电位发生变化,且电位的信号开始累加】
7.2 感知机
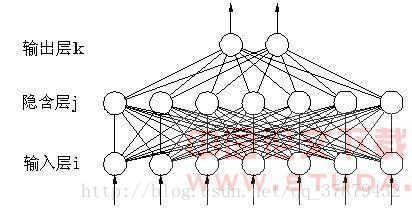
如图是单层感知机模型(只有输入层和输出层)。单层感知机本质上是高维空间中,构造出来的合理的边界超平面(b+sum(wixi),把不同类别的数据集分离。因此对于线性可分,或者近似线性可分的数据集有很好的效果。
异或问题属于线性不可分问题。
多层感知机(MLP):1991年提出的全局逼近定理为我们提供了理论依据:对于一个含有隐藏层的前馈神经网络,如果隐藏层可以由任意多的神经元组成,那么神经网络能够逼近实数范围内的任意连续函数。
对于分类问题,隐藏层的作用就是把线性不可分的数据,通过线性变换(预激活阶段)和非线性变换(激活阶段)的操作,使得数据变为线性可分。
7.3激活函数
激活函数是神经网络设计的一个核心单元。在神经网络中,把处于在活跃状态的神经元称为激活态,处于非活跃状态的神经元称为抑制态。激活函数赋予了神经元自我学习和适应的能力。
激活函数的作用是为了在神经网络中引入非线性的学习和处理能力。
常用的激活函数(满足1 非线性 2 可微性 3 单调性)
1 sigmoid函数
2 tanh函数
3 ReLU函数
7.4 反向传播和梯度消失
反向传播算法(BP算法)仍然是当前神经网络最受欢迎的优化方法。
反向传播由前向和后向两个操作构成。
前向传播利用当前的权重参数和输入数据,从下往上(即从输入层到输出层),求取预测结果,并利用预测结果与真实值求解出损失函数的值。
反向操作则是利用前向操作求解损失函数,从上往下(输出到输入),求解网络的参数梯度。
经过前向和反向两个操作后,完成一次迭代过程。
损失函数
机器学习算法有模型,策略和算法三个要素构成。当选择一种算法模型后,下一步需要考虑的使用什么样的策略或准则来选择最优模型。
损失函数是机器学习用来衡量一次预测结果好坏的函数,它是一个非负实数值函数。用L(Y,f(X))来表示,常用的损失函数有四种。
1 0-1损失函数 比较的是预测值F(x)与真实值Y是否相同。
0-1损失函数是一个非凸函数,在求解过程中,存在很多不足,而且它只关心预测值和真实值是否相同。没有考虑预测值和真实值之间的距离。因而只做指标,不具有优化。
2 平方损失函数 是线性回归模型最常用的最优化的目标函数。
3 对数损失函数 常用与分类模型的最优化目标函数
4 HInge损失函数 有时也称最大间隔目标函数,是SVM采用的最优化目标函数
欠拟合(梯度消失)
梯度消失:根源在于激活函数,回顾前面参数的求导过程。对预激活输出求导都牵扯到激活函数的求导,传统的激活函数(如sigmoid )函数为列。
它的导数的范围都小于1 sigmoid的函数的取值范围是【0,1/4】也就是说,每对激活函数求导,该层比上一层减少1/4。这样梯度的计算是随着层数的增加而呈现指数级的递减趋势,离输出层越远,梯度减少的越明显。
为了防止神经网络在训练过程中梯度消失的问题。
采用合理的激活函数,如ReLU ,maxout来取代传统的sigmoid函数。
过拟合
过拟合是机器学习中常见的难题。过拟合一般指的是在模型选择的过程中,选择的模型参数过多,导致对训练数据的预测很好,但对未知数据的预测很差的现象。
在深度神经网络中,网络的层数更深,而训练的样本往往更少。过拟合往往很严重。
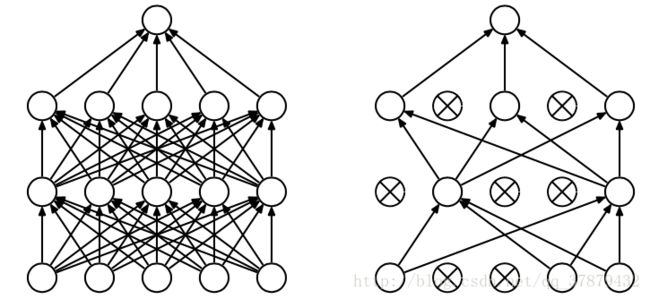
Dropout结合单模型和多模型的优点,是解决过拟合一个强有力的武器。
Dropout的思想是每一层迭代的过程中,会随机让网络某些节点(神经元)不参与训练,同时把这些暂时丢弃的神经元的相关的所有边全部去掉,相应的权重不会在这一次迭代中更新,每次迭代训练都会重复这个操作。
丢掉的神经元只是暂时不更新,下一次迭代会重新参与随机化的Dropout。