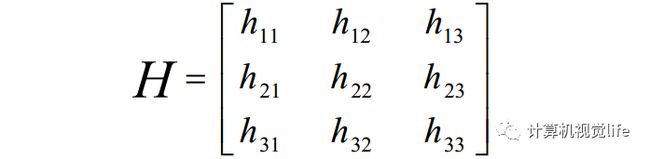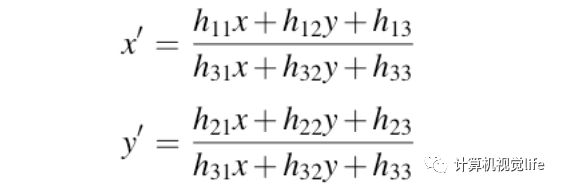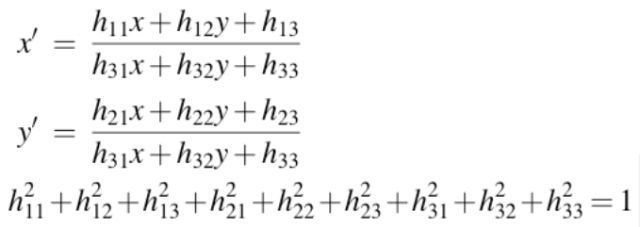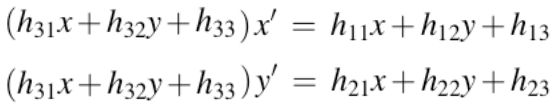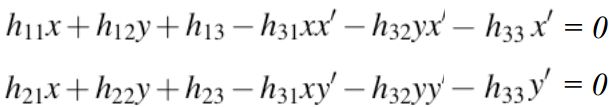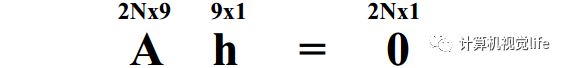单应性变换

转载http://www.sohu.com/a/223594989_100007727

单应性

单应性变换，可简单理解为用来描述物体在世界坐标系和像素坐标系之间的位置映射关系，对应的变换矩阵称为单应性矩阵。

单应性在计算机视觉中的应用

单应性在图像校正、图像拼接、相机位姿估计、视觉SLAM等领域有非常重要的作用。

1.图像校正

    用单应性矩阵进行图像校正，如下图所示，至少需要四个对应点就可以实现。

2.视角变换

    单应性矩阵用于视角变换，如下图所示，可将左边普通视图转换为右边的俯瞰视图

3.图像拼接

    使用单应性矩阵，将不同角度拍摄的图像都转换到同一视角下，实现图像拼接。如下图所示，使用单应性矩阵可以将image1和image2都变换到同一平面。

 

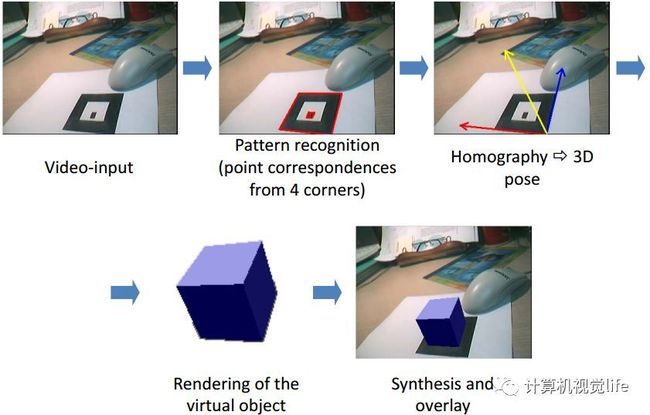
4.增强现实（AR）

    平面二维标记图案（marker）经常用来做AR展示。根据marker不同视角下的图像可以方便的得到虚拟物体的位置姿态并进行显示，如下图所示。

如何估计单应矩阵？

    首先，假设两张图像中的对应点对对齐次坐标为（x',y',1）和（x,y,1），单应矩阵H定义为：

则有：

矩阵展开后有3个等式，将第3个等式代入前两个等式中可得：

也就是说，一个点对对应两个等式。

单应矩阵H有几个自由度？

    8个，如果给定一个单应矩阵H，给它的元素乘上同一个数，得到的单应a*H和H的作用相同，因为新单应矩阵无非把齐次点x1变成了齐次点a*x1，都是一回事。因此可以把a假设成1/h22，那么H就变成了只有8个自由元素的矩阵。

8自由度下H计算过程有两种方法

第一种，直接设置h33=1，上述等式变为

第二种，给H添加约束条件，将H矩阵模变为1，如下

以第二种方法继续推导，将上述等式乘以分母展开，得到如下，

整理得到，得到

假如已知两幅图片中对应的N个点对（特征点匹配对），可以得到如下线性方程组，

写成矩阵形式，

    由于单应矩阵H包含了||H||=1约束，因此根据上图的线性方程，8自由度的H我们至少需要4对对应的点才能计算出单应矩阵，这也回答了前面图像校正中提到的为何至少需要四个点对的根本原因。然而，在真实的应用场景中，计算的点对中都会包含噪声，比如点的位置偏差几个像素，甚至出现特征点对误匹配的现象，如果只使用4个点对来计算单应矩阵，那会出现很大的误差。因此，为了使得计算更精确，一般都会使用远大于4个点对来计算单应矩阵。另外上述方程组采用直接线性解法通常很难得到最优解，所以实际中一般会用其他优化方法。如奇异值分解，LM算法等进行求解。

总结一下大致过程，

    1.打印一张棋盘格标定图纸，将其贴在平面物体的表面。

    2.拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现。

    3.对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点（角点，也就是下图中黑白棋盘交叉点，中间品红色的圆圈内就是一个角点）。我们定义打印的棋盘图纸位于世界坐标系Zw=0的平面上，世界坐标系的原点位于棋盘图纸的固定一角（比如下图中黄色点）。像素坐标系原点位于图片左上角。

    4.因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对（越多计算结果越鲁棒），就可以根据LM等优化方法得到其单应矩阵H。

注：计算单应矩阵一般不需要自己写函数实现，OpenCV中就有现成的函数可以调用，对应的C++函数是：

             Mat findHomography(InputArray srcPoints, InputArray dstPoints, int method=0,

                      double ransacReprojThreshold=3, OutputArray mask=noArray() )

从函数的定义来看，只要输入匹配点对，指定具体计算方法即可输出结果。