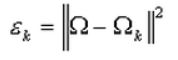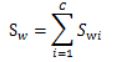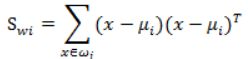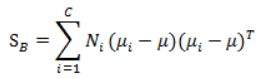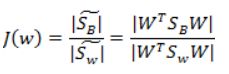基于PCA和LDA的人脸识别

一、系统设计

1.1研究背景及意义

随着信息技术的不断发展,人们对方便快捷的身份验证和识别系统的要求不断提高。人脸识别技术因具有直接、友好、快捷、方便、易为用户所接受等特点,成为了身份验证的最理想依据,也早已成为了模式识别领域研究的热点。众多科研人员通过多年潜心研究,也做出了许多的成果,但是在实际应用中,现有的人脸识别产品大多因识别率不高、稳定性差等缺点无法满足实际需要。

针对这一现状,本文研究了EigenFace、FisherFace两种人脸特征提取算法,在此基础上设计了基于PCA+LDA算法的人脸识别新方案,并对PCA+LDA算法做了改进。同时还对PCA特征子空间的维数与识别率的关系进行了研究。

1.2系统开发环境

软件环境：Windows10

1.3系统使用工具

PyCharm2018.3+Anaconda3+OpenCV

1.4系统功能需求

①人脸检测：调用分类器，将人脸从一张图片中分析并用适当的框架标识出来

②数据库存储：能够根据情况更新人脸数据库中的数据，用于训练；

③人脸识别：能够根据数据库中所存储的人脸信息，识别出输入的未知人脸

④动态识别：通过摄像头的视频捕捉，能够实时地识别出每一帧图像中的人脸图像

• 界面设计：需要设计对程序的输入输出显示的功能进行界面的设计

1.5系统数据设计

数据来源：

• yale人脸数据库：其中共有165张100*100的bmp格式灰度图像，分为15人，每人11张

② 通过调用摄像头自行拍摄的照片，分为2人。每人11张。

二、算法思想

2.1EigenFace特征脸法

EigenFace是基于PCA（主成分分析）的人脸识别算法。PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。一般情况下，在数据挖掘和机器学习中，数据被表示为向量。很多机器学习算法的复杂度和数据的维数有着密切关系，甚至与维数呈指数级关联。如果维数较小，也许还无所谓，但是实际机器学习中处理成千上万甚至几十万维的情况也并不罕见，在这种情况下，机器学习的资源消耗是不可接受的，因此我们必须对数据进行降维。

主成分分析（PCA）的原理就是将一个高维向量x，通过一个特殊的特征向量矩阵U，投影到一个低维的向量空间中，表征为一个低维向量y，并且仅仅损失了一些次要信息。也就是说，通过低维表征的向量和特征向量矩阵，可以基本重构出所对应的原始高维向量，如图1。

 

图2-1

在人脸识别中，特征向量矩阵U称为特征脸（EigenFace）空间，因此其中的特征向量ui进行量化后可以看出人脸轮廓。

2.2FisherFace方法

假设有C个人的人脸图像，每个人可以有多张图像，所以按人来分，可以将图像分为C类，这节就是要解决如何判别这C个类的问题。判别之前需要先处理下图像，将每张图像按照逐行逐列的形式获取像素组成一个向量，和第一节类似设该向量为x，设向量维数为n，设x为列向量（n行1列）。这里的n有可能成千上万，比如100x100的图像得到的向量为10000维，所以第一节里将x投影到一个向量的方法可能不适用了，比如图2：

 

图2-2

平面内找不到一个合适的向量，能够将所有的数据投影到这个向量而且不同类间合理的分开，所以我们需要增加投影向量w的个数。

FisherFace是基于线性判别分析（Linear Discriminant Analysis, 以下简称LDA）。LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

三、算法实现

3.1EigenFace实现步骤

(1)获取包含M张人脸图像的集合dataMat，每张图转化为一列，将每一列进行合并，转为矩阵，最后得到图像矩阵dataMat。

(2)计算平均图像，对行求均值后得到平均脸矩阵MeanMat，若还原回像素矩阵如图3-1，并获得偏差矩阵。每张人脸都减去这个平均图像，最后得到偏差矩阵diffMat。

   

图3-1求均值后得到的平均脸

(3)求协方差矩阵,并计算特征值和特征向量。但是在这里，协方差矩阵的维度过大，无法计算，计算量大且无法储存，因此使用如下的方法：

设 T 是预处理图像的矩阵，每一列对应一个减去均值图像之后的图像。则，协方差矩阵为  ，并且对 S 的特征值分解为

 

然而， 是一个非常大的矩阵。因此，如果转而使用如下的特征值分解

   

 

此时，我们发现如果在等式两边乘以T，可得到

这就意味着，如果 ui 是的一个特征向量，则是 S 的一个特征向量。

这里的T 就是偏差矩阵，最后我们得的一个特征向量，再用T与之相乘就是协方差矩阵的特征向量u。而此时我们求的特征向量每一行如果变成图像大小的矩阵，就可以看做是一个新的人脸，称为特征脸，如图4-2。

图4-2 特征脸

(4)由于当前问题是小样本问题，即样本维数远远大于样本数，而特征值分解仅适用于方阵，因此这里我们需要用到与特征值分解原理相同，但是适用于任意矩阵特征值的奇异值分解得到协方差矩阵特征向量。

假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵

A的SVD为：

其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足UTU=I,VTV=I。

(5)主成分分析。在求得的特征向量和特征值中，越大的特征值对于我们区分越重要，也就是我们说的主成分，我们只需要那些大的特征值对应的特征向量，而那些十分小甚至为0的特征值对于我们来说，对应的特征向量几乎没有意义。在这里我们选取的特征向量维数是40维，在大多数应用中，40维已经足够代表样本的特征。

(6) 进行人脸识别。此时我们导入一个新的人脸，我们使用上面主成分分析后得到的特征向量，来求得一个每一个特征向量对于导入人脸的权重向量。利用求得导入人脸的权重向量与样本集的权重向量的欧氏距离，来判断未知人脸与训练人脸之间的差距。欧氏距离：

3.2FisherFace实现步骤

(1)与PCA类似，得到训练集dataMat及需要降至的维度d(d=classNum-1)，减去均值，得到偏差矩阵。

(2)计算类内散度矩阵Sw，Sw定义如下：

其中，

代表类别i的类内散列度，它是一个m×n的矩阵。

(3)计算类间散度矩阵SB，SB定义如下：

代表每个类别到μ距离的加和，Ni代表类别内i的个数classInnum，也就是某个人的人脸图像个数。

(4)投影方向是多维，求每类中心相对于全样本中心的散列度之和，得到：

最后化为：

同PCA类似，求解矩阵的特征向量，然后取前d个特征值最大的特征向量。

四、算法改进

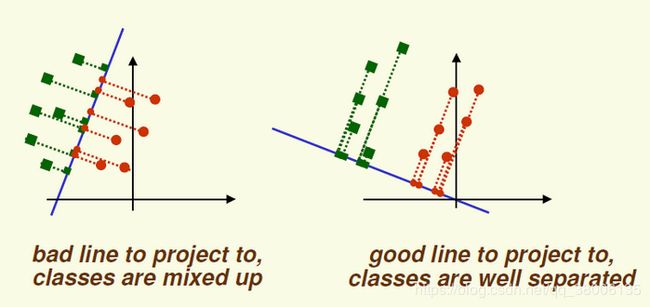
图4-1

通过PCA降维后的数据不能进行分类，与LDA相比缺少一个独立标识每个数据的标签label。做回归时，如果特征太多，会产生不相关特征引入、过度拟合等问题。如图4-1左，PCA所做的只是将整组数据整体映射到最方便这组数据的坐标轴上，映射时没有利用任何数据内部的分类信息。因此，虽然采用了PCA进行降维，整组数据在表示上更加方便（降低了维数并将信息损失降到最低），但在分类上会变得更加困难。如图4-1右，在增加了分类之后，两组输入映射到了另外一个坐标轴上，有了这样一个映射，两组数据之间的就变得更易区分了(在低维上就可以区分，减少了很大的运算量)。

但是，在当前实验中，我们对LDA算法进行了改进，LDA降维采用的数据集并不是原始的照片，而是PCA降维后的值，原因如下：

(1)通过PCA降维后数据量会明显减少，提高程序性能。

(2)多重共线性预测变量之间相互关联，多重共线性空间会导致解空间的不稳定，从而导致结果的不连贯。

(3)高维空间本身具有稀疏性，一维正态分布有68%的值落于正负标准差之间，而在十维空间上只有0.02%，过多的变量会妨碍查找规律的建立。

(4)仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。

五、结果及分析

共进行了十次测试，每次用十张新的照片与库中的照片进行比对，最后得到正确率。

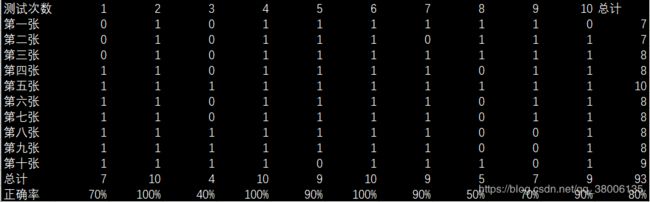
5.1EigenFace正确率测试

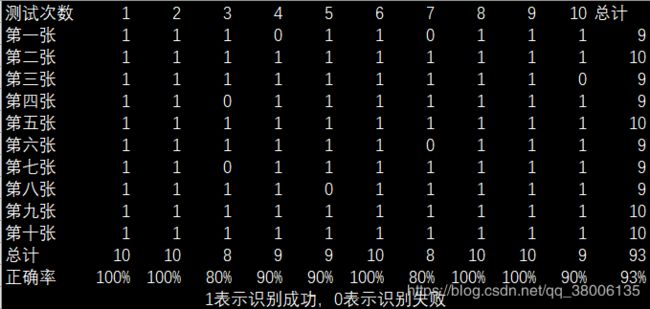
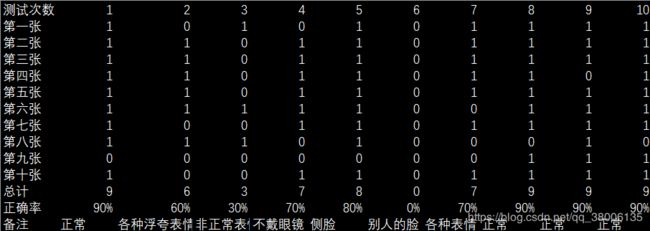
5.2改进后的FisherFace正确率测试

5.3对比及分析

可以明显看出，改进后的算法正确率要高得多。

但是由于算法本身的限制，如果要得到更准确的结果，对样本的要求较高，光照、人的表情等各个方面都需要考虑，因此我们更换了不同的样本进行测试，来研究样本的选取。

当样本选取正常表情、光照较明亮时，正确率很高；当样本中人脸表情较浮夸，测试时人的表情正常时，准确率较低。因此，样本集应该尽量多地包括到人脸的各种表情及考虑到光照，应该尽量光线明亮。

另外，在降维的维数选择上，我们进行了测试，来判断对当前应用来说，选取多少维是合适的。

对当前应用来说，维数选取22维已经可以代表特征，但是为了程序的可扩展性，我们还是选取了最佳的40维。

 

 

参考文献

[1]Dan Kalman.A Singularly Valuable Decomposition:The SVD of a Matrix·http://www-users.math.umn.edu/~lerman/math5467/svd.pdf

[2]J.R.Parker.图像处理与计算机视觉算法及应用(第2版):清华大学出版社，2012

[3]A Tutorial on Principal Component Analysis·https://www.cs.cmu.edu/~elaw/papers/pca.pdf

[4]周志华.机器学习.清华大学出版社，2016

[5]基于PCA和LDA的人脸识别技术的研究.伍威 李晋惠. http://www.docin.com/p-1385093618.html

 

github地址：https://github.com/Gonlandoo/Face_Recognition

给个星哟