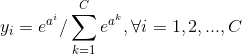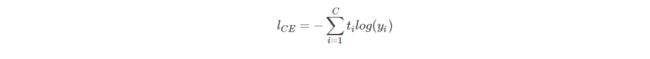SoftMax函数，交叉熵损失函数与熵，对数似然函数

深度学习以及机器学习中都会用到SoftMax函数，交叉熵损失函数与熵，对数似然函数等一些数学方面的知识，此文作为个人学习笔记。

1.softmax函数

（1）定义

多分类问题中，我们可以使用SoftMax函数，对输出的值归一化为概率值，映射到（0，1）区间。

这里假设在进入softmax函数之前，已经有模型输出C值，其中C是要预测的类别数，模型可以是全连接网络的输出a，其输出个数为C，即输出为a1,a2,...,aC。

所以对每个样本，它属于类别ii的概率为： 

经过上式的运算之后，yi被归一化到了[0,1]区间，并且所有类别的yi之和为1.

（2)导数

对softmax函数进行求导，其中aj(j=1,2,..i,...C)是自变量，yi是因变量。实际上所求取的应当是yi对aj的偏导：

所以求偏导分为两种情况：i是否等于j。

 

这样就得到了softmax函数对于变量的偏导数。这在后续的计算损失函数的偏导时会用到。

 

2.熵，相对熵与交叉熵

（1）信息量  

         

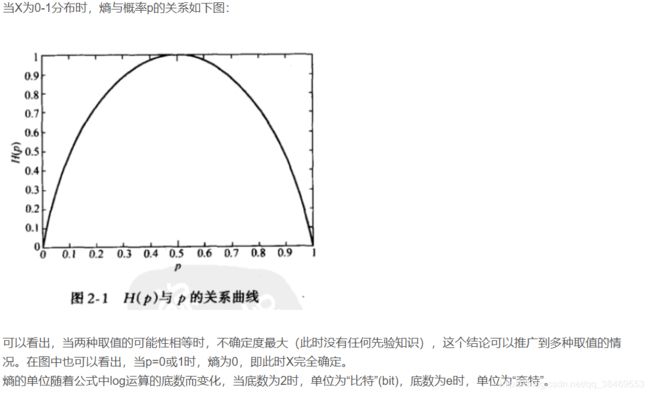
（2）熵

在某次考试结果公布前，小明的考试结果有多大的不确定度呢？你肯定会说：十有八九不及格！因为根据先验知识，小明及格的概率仅有0.1,90%的可能都是不及格的。怎么来度量这个不确定度？求期望！不错，我们对所有可能结果带来的额外信息量求取均值（期望），其结果就能够衡量出小明考试成绩的不确定度了。

   

    

（3）相对熵

  

（4）交叉熵

   

注意：

上述最后得到的交叉熵损失函数是基于“p和q都服从0-1分布”而推出来的。而实际在神经网络中，对于某个样本进行分类预测时，预测值和真实值（标签值）都服从0-1分布，如下所述：

回到我们多分类的问题上，真实的类标签可以看作是分布，对某个样本属于哪个类别可以用One-hot的编码方式，是一个维度为C的向量，比如在5个类别的分类中，[0, 1, 0, 0, 0]表示该样本属于第二个类，其概率值为1。我们把真实的类标签分布记为p，该分例子中，当第i个样本的ti=1时表示该样本属于该类别。

同时，分类模型经过softmax函数之后，也是一个概率分布，所以我们把模型的输出的分布记为q，它也是一个维度为C的向量，例如现在q的分布为：[0.1, 0.8, 0.05, 0.05, 0]。 

此时用样本真实标签值与预测值的交叉熵就可以作为损失函数了：

对于所有的类别求损失之和：

（5）损失函数求导

    

上述就是多分类问题中损失函数对于单个输出aj的偏导数，后续进行权重更新时进行反向传播就会用到这个偏导。

 

3.对数似然函数

机器学习里面，对模型的训练都是对Loss function进行优化，在分类问题中，我们一般使用最大似然估计（Maximum likelihood estimation）来构造损失函数。对于输入的x，其对应的类标签为t，我们的目的是找到使p(t|x)最大的模型f(x),y=f(x)为模型的预测值。

在二分类问题中：

可以看到，多分类问题中，上述通过最大似然估计得到的损失函数与通过交叉熵得到的损失函数相同。

 

参考：

https://blog.csdn.net/behamcheung/article/details/71911133

https://blog.csdn.net/rtygbwwwerr/article/details/50778098#commentBox