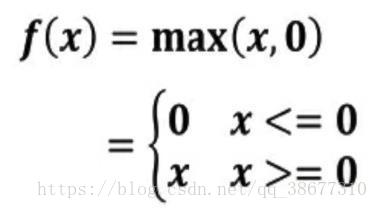Tensorflow笔记——(四)神经网络优化
神经元模型:用数学公式表示为:f(xw+b),f () 为激活函数。神经网络是以神经元为基本单元构成的。
激活函数:引入非线性激活因素,提高模型的表达力。
常用的激活函数有 relu、sigmoid、tanh 等。
① 激活函数 relu: 在 Tensorflow 中,用 tf.nn.relu()表示
relu()数学表达式 relu()数学图形
② 激活函数 sigmoid:在 Tensorflow 中,用 tf.nn.sigmoid()表示
sigmoid ()数学表达式 sigmoid()数学图形
③ 激活函数 tanh:在 Tensorflow 中,用 tf.nn.tanh()表示
tanh()数学表达式 tanh()数学图形
神经网络的复杂度:可用神经网络的层数和神经网络中待优化参数个数表示
神经网路的层数:一般不计入输入层,层数 = n 个隐藏层 + 1 个输出层
神经网路待优化的参数:神经网络中所有参数 w 的个数 + 所有参数 b 的个数
例如:
输入层 隐藏层 输出层
在该神经网络中,包含 1 个输入层、1 个隐藏层和 1 个输出层,该神经网络的层数为 2 层。
在该神经网络中,参数的个数是所有参数 w 的个数加上所有参数 b 的总数,第一层参数用三行四列的二阶张量表示(即 12 个线上的权重 w)再加上 4 个偏置 b;第二层参数是四行两列的二阶张量()即
8 个线上的权重 w再加上 2 个偏置 b。总参数 = 3*4+4 + 4*2+2 = 26。
损失函数(loss):用来表示预测值(y)与已知答案(y_)的差距。在训练神经网络时,通过不断改变神经网络中所有参数,使损失函数不断减小,从而训练出更高准确率的神经网络模型。
常用的损失函数有均方误差、自定义和交叉熵等。
①均方误差 mse:n 个样本的预测值 y 与已知答案 y_之差的平方和,再求平均值。
在 Tensorflow 中用 loss_mse = tf.reduce_mean(tf.square(y_ - y))
例如:
预测酸奶日销量 y,x1 和 x2 是影响日销量的两个因素。
应提前采集的数据有:一段时间内,每日的 x1 因素、x2 因素和销量 y_。采集的数据尽量多。在本例中用销量预测产量,最优的产量应该等于销量。由于目前没有数据集,所以拟造了一套数
据集。利用 Tensorflow 中函数随机生成 x1、 x2,制造标准答案 y_ = x1 + x2,为了更真实,求和后还加了正负 0.05 的随机噪声。
我们把这套自制的数据集喂入神经网络,构建一个一层的神经网络,拟合预测酸奶日销量的函数。
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
rdm = np.random.RandomState(SEED)
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)]for (x1, x2) in X]
#定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
#定义损失函数及反向传播方法。
#定义损失函数为MSE,反向传播方法为梯度下降。
loss_mse = tf.reduce_mean(tf.square(y_ - y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
#生成会话,训练STEPS轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 20000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 32
end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
sess.run(train_step, feed_dict={x : X[start : end], y_ : Y_[start : end]})
if i % 500 == 0:
print("After {:} training steps, w1 is: ".format(i))
print(sess.run(w1),"\n")
print("Final w1 is:\n",sess.run(w1))运行结果:
After 19000 training steps, w1 is:
[[0.974931 ] [1.0206276]]
After 19500 training steps, w1 is:
[[0.9777026] [1.0181949]]
Final w1 is:
[[0.98019385] [1.0159807 ]]由上述代码可知,本例中神经网络预测模型为 y = w1*x1 + w2*x2,损失函数采用均方误差。通过使损失函数值(loss)不断降低,神经网络模型得到最终参数 w1=0.98,w2=1.02,销量预测结果为 y = 0.98*x1 + 1.02*x2。由于在生成数据集时,标准答案为 y = x1 + x2,因此,销量预测结果和标准答案已非常接近,说明该神经网络预测酸奶日销量正确。
②自定义损失函数:根据问题的实际情况,定制合理的损失函数。
例如:
对于预测酸奶日销量问题,如果预测销量大于实际销量则会损失成本;如果预测销量小于实际销量则会损失利润。在实际生活中,往往制造一盒酸奶的成本和销售一盒酸奶的利润是不等价的。因此,需要使用符合该问题的自定义损失函数。
自定义损失函数为:loss = ∑fn(y_, y)
其中,损失定义成分段函数:
f(y_, y) = profit * (y_-y) y_ > y
cost *(y-y_) y >= y_
损失函数表示,若预测结果 y 小于标准答案 y_,损失函数为利润乘以预测结果 y 与标准答案 y_之差;若预测结果 y 大于标准答案 y_,损失函数为成本乘以预测结果 y 与标准答案 y_之差。
用 Tensorflow 函数表示为:
loss = tf.reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))
1、 若酸奶成本为 1 元,酸奶销售利润为 9 元,则制造成本小于酸奶利润,因此希望预测的结果 y 多一些。采用上述的自定义损失函数,训练神经网络模型。
#酸奶成本1元,酸奶利润9元
#预测少了损失大,故不要预测少,故生成的模型会多预测一些
#导入模块,生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
COST = 1
PROFIT = 9
rdm = np.random.RandomState(SEED)
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)]for (x1, x2) in X]
#定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
#定义损失函数及反向传播方法。
#定义损失函数为MSE,反向传播方法为梯度下降。
#定义损失函数使得预测少了的损失大,于是模型应该偏向多的方向预测
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_)*COST, (y_ - y)*PROFIT))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
#生成会话,训练STEPS轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 20000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 32
end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
sess.run(train_step, feed_dict={x : X[start : end], y_ : Y_[start : end]})
if i % 500 == 0:
print("After {:} training steps, w1 is: ".format(i))
print(sess.run(w1),"\n")
print("Final w1 is:\n",sess.run(w1))运行结果:
After 19000 training steps, w1 is:
[[1.0171654]
[1.038825 ]]
After 19500 training steps, w1 is:
[[1.0208615]
[1.0454264]]
Final w1 is:
[[1.020171 ]
[1.0425103]]由代码执行结果可知,神经网络最终参数为 w1=1.03, w2=1.05,销量预测结果为 y =1.03*x1 +
1.05*x2。由此可见,采用自定义损失函数预测的结果大于采用均方误差预测的结果,更符合实际需求。
2、若酸奶成本为 9 元,酸奶销售利润为 1 元,则制造成本大于酸奶利润,因此希望预测结果 y 小一些。采用上述的自定义损失函数,训练神经网络模型。
#酸奶成本9元,酸奶利润1元
#预测少了损失大,故不要预测少,故生成的模型会多预测一些
#导入模块,生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
COST = 9
PROFIT = 1
rdm = np.random.RandomState(SEED)
X = rdm.rand(32, 2)
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)]for (x1, x2) in X]
#定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
#定义损失函数及反向传播方法。
#定义损失函数为MSE,反向传播方法为梯度下降。
#重新定义损失函数,使得预测多了的损失大,于是模型应该偏向少的方向预测
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_)*COST, (y_ - y)*PROFIT))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
#生成会话,训练STEPS轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 20000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 32
end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
sess.run(train_step, feed_dict={x : X[start : end], y_ : Y_[start : end]})
if i % 500 == 0:
print("After {:} training steps, w1 is: ".format(i))
print(sess.run(w1),"\n")
print("Final w1 is:\n",sess.run(w1))After 19000 training steps, w1 is:
[[0.9630599]
[0.976308 ]]
After 19500 training steps, w1 is:
[[0.967159 ]
[0.97354174]]
Final w1 is:
[[0.9661967 ]
[0.97694933]]由执行结果可知,神经网络最终参数为 w1=0.96,w2=0.97,销量预测结果为 y =0.96*x1 + 0.97*x2。因此,采用自定义损失函数预测的结果小于采用均方误差预测的结果,更符合实际需求。
3、交叉熵(Cross Entropy):表示两个概率分布之间的距离。交叉熵越大,两个概率分布距离越远,两个概率分布越相异;交叉熵越小,两个概率分布距离越近,两个概率分布越相似。
交叉熵计算公式:H(y_ , y) = −∑y_ ∗ log y
用 Tensorflow 函数表示为:ce= -tf.reduce_mean(y_* tf.log(tf.clip_by_value(y, 1e-12, 1.0)))
例如:
两个神经网络模型解决二分类问题中,已知标准答案为 y_ = (1, 0),第一个神经网络模型预测结果为
y1=(0.6, 0.4),第二个神经网络模型预测结果为 y2=(0.8, 0.2),判断哪个神经网络模型预测的结果更接近标准答案。
根据交叉熵的计算公式得:
H1((1,0),(0.6,0.4)) = -(1*log0.6 + 0*log0.4) ≈ -(-0.222 + 0) = 0.222
H2((1,0),(0.8,0.2)) = -(1*log0.8 + 0*log0.2) ≈ -(-0.097 + 0) = 0.097
由于 0.222>0.097,所以预测结果 y2 与标准答案 y_更接近,y2 预测更准确。
softmax 函数:将 n 分类的 n 个输出(y1,y2…yn)变为满足以下概率分布要求的函数。
softmax 函数应用:在 n 分类中,模型会有 n 个输出,即 y1,y2…yn,其中 yi 表示第 i 种情况出现的可能性大小。将 n 个输出经过 softmax 函数,可得到符合概率分布的分类结果。
在 Tensorflow 中,一般让模型的输出经过 sofemax 函数,以获得输出分类的概率分布,再与标准答案对比,求出交叉熵,得到损失函数,用如下函数实现:
ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
cem = tf.reduce_mean(ce)
学习率 learning_rate:表示了每次参数更新的幅度大小。学习率过大,会导致待优化的参数在最小值附近波动,不收敛;学习率过小,会导致待优化的参数收敛缓慢。
在训练过程中,参数的更新向着损失函数梯度下降的方向。参数的更新公式为:
假设损失函数为 loss = (w + 1)^2。梯度是损失函数 loss 的导数为 ∇=2w+2。如参数初值为 5,学习率为 0.2,则参数和损失函数更新如下:
1 次 参数 w:5 5 - 0.2 * (2 * 5 + 2) = 2.6
2 次 参数 w:2.6 2.6 - 0.2 * (2 * 2.6 + 2) = 1.16
3 次 参数 w:1.16 1.16 – 0.2 * (2 * 1.16 + 2) = 0.296
4 次 参数 w:0.296
损失函数 loss = (w + 1)2 的图像为:
由图可知,损失函数 loss 的最小值会在(-1,0)处得到,此时损失函数的导数为 0,得到最终参数 w = -1。
#设损失函数 loss=(w+1)^2,令w初值是常数5
#反向传播就是求最优w,即最小loss对应的w值
import tensorflow as tf
#定义待优化参数w初值赋5
w = tf.Variable(tf.constant(5, dtype=tf.float32))
#定义损失函数loss
loss = tf.square(w+1)
#定义反向传播方法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#生成会话,训练40轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
for i in range(40):
sess.run(train_step)
w_val = sess.run(w)
loss_val = sess.run(loss)
print("After {} steps: w is {}, loss is {}".format(i, w_val, loss_val)) 运行结果:
After 33 steps: w is -0.9999998211860657, loss is 3.197442310920451e-14
After 34 steps: w is -0.9999998807907104, loss is 1.4210854715202004e-14
After 35 steps: w is -0.9999999403953552, loss is 3.552713678800501e-15
After 36 steps: w is -0.9999999403953552, loss is 3.552713678800501e-15
After 37 steps: w is -0.9999999403953552, loss is 3.552713678800501e-15
After 38 steps: w is -0.9999999403953552, loss is 3.552713678800501e-15
After 39 steps: w is -0.9999999403953552, loss is 3.552713678800501e-15学习率的设置
学习率过大,会导致待优化的参数在最小值附近波动,不收敛;学习率过小,会导致待优化的参数收敛缓慢。
例如:
① 对于上例的损失函数 loss = (w + 1)^2。则将上述代码中学习率修改为 1,其余内容不变。实验结果如下:
After 33 steps: w is -7, loss is 36
After 34 steps: w is 5, loss is 36
After 35 steps: w is -7, loss is 36
After 36 steps: w is 5, loss is 36
After 37 steps: w is -7, loss is 36
After 38 steps: w is 5, loss is 36
After 39 steps: w is -7, loss is 36由运行结果可知,损失函数 loss 值并没有收敛,而是在 5 和-7 之间波动。
② 对于上例的损失函数 loss = (w + 1)2。则将上述代码中学习率修改为 0.0001,其余内容不变。实验结果如下:
After 33 steps: w is 4.953, loss is 35.546
After 34 steps: w is 4.952, loss is 35.549
After 35 steps: w is 4.956, loss is 35.542
After 36 steps: w is 4.923, loss is 35.541
After 37 steps: w is 4.955, loss is 35.542
After 38 steps: w is 4.951, loss is 35.542
After 39 steps: w is 4.952, loss is 35.542由运行结果可知,损失函数 loss 值缓慢下降,w 值也在小幅度变化,收敛缓慢。
指数衰减学习率:学习率随着训练轮数变化而动态更新
用 Tensorflow 的函数表示为:
global_step = tf.Variable(0, trainable=False) learning_rate = tf.train.exponential_decay( LEARNING_RATE_BASE,
global_step,
LEARNING_RATE_STEP, LEARNING_RATE_DECAY,
staircase=True/False)
其中,LEARNING_RATE_BASE 为学习率初始值,LEARNING_RATE_DECAY 为学习率衰减率,global_step 记录了当前训练轮数,为不可训练型参数。学习率 learning_rate 更新频率为输入数据集总样本数除以每次喂入样本数。若 staircase 设置为 True 时,表示 global_step / learning rate step 取整数,学习率阶梯型衰减;若 staircase 设置为 false 时,学习率会是一条平滑下降的曲线。
例如:
在本例中,模型训练过程不设定固定的学习率,使用指数衰减学习率进行训练。其中,学习率初值设置为 0.1,学习率衰减率设置为 0.99,BATCH_SIZE 设置为 1。
#设损失函数 loss=(w+1)^2,令w初值是常数10
#反向传播就是求最优w,即最小loss对应的w值
#使用指数衰减的学习率,在迭代初期得到较高的下降速度
#可以在较小的训练轮数下取得更有收敛度
import tensorflow as tf
LEARNING_RATE_BASE = 0.1 #最初学习率
LEARNING_RATE_DECAY = 0.99 #学习率衰减率
LEARNING_RATE_STEP = 1 #喂入多少轮BATCH_SIZE后,更新一次学习率,一般设为:总样本数/BATCH_SIZE
#运行了几轮BATCH_SIZE的计数器,初值给0,设为不被训练
global_step = tf.Variable(0, trainable=False)
#定义指数下降学习率
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, LEARNING_RATE_STEP, LEARNING_RATE_DECAY, staircase=True)
#定义待优化参数,初始值给5
w = tf.Variable(tf.constant(5, dtype=tf.float32))
#定义损失函数loss
loss = tf.square(w+1)
#定义反向传播方法
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
#生成会话,训练40轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
for i in range(40):
sess.run(train_step)
learning_rate_val = sess.run(learning_rate)
global_step_val = sess.run(global_step)
w_val = sess.run(w)
loss_val = sess.run(loss)
print(i, learning_rate_val, global_step_val, w_val, loss_val)运行结果:
33 0.071055345 34 -0.98955023 0.00010919763
34 0.0703448 35 -0.9910353 8.036616e-05
35 0.069641344 36 -0.9922965 5.9343653e-05
36 0.06894493 37 -0.99336946 4.396406e-05
37 0.068255484 38 -0.99428374 3.2675678e-05
38 0.06757293 39 -0.9950641 2.436331e-05
39 0.066897206 40 -0.9957312 1.8222867e-05由结果可以看出,随着训练轮数增加学习率在不断减小。
滑动平均:记录了一段时间内模型中所有参数 w 和 b 各自的平均值。利用滑动平均值可以增强模型的泛化能力。
滑动平均值(影子)计算公式: 影子 = 衰减率 * 影子 +(1 - 衰减率)* 参数
用 Tesnsorflow 函数表示为:
ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY,global_step)
其中,MOVING_AVERAGE_DECAY 表示滑动平均衰减率,一般会赋接近 1 的值,global_step 表示当前训练了多少轮。
ema_op = ema.apply(tf.trainable_variables())
其中,ema.apply()函数实现对括号内参数求滑动平均,tf.trainable_variables()函数实现把所有待训练参数汇总为列表。
with tf.control_dependencies([train_step, ema_op]):
train_op = tf.no_op(name='train')
其中,该函数实现将滑动平均和训练过程同步运行。
查看模型中参数的平均值,可以用 ema.average()函数。 例如:
在神经网络模型中,将 MOVING_AVERAGE_DECAY 设置为 0.99,参数 w1 设置为 0,w1 的滑动平均值设置为 0。
①开始时,轮数 global_step 设置为 0,参数 w1 更新为 1,则 w1 的滑动平均值为:
w1 滑动平均值=min(0.99,1/10)*0+(1– min(0.99,1/10)*1 = 0.9
③ 当轮数 global_step 设置为 100 时,参数 w1 更新为 10,以下代码 global_step 保持为 100,每次执行滑动平均操作影子值更新,则滑动平均值变为:
w1 滑动平均值=min(0.99,101/110)*0.9+(1– min(0.99,101/110)*10 = 0.826+0.818=1.644
③再次运行,参数 w1 更新为 1.644,则滑动平均值变为:
w1 滑动平均值=min(0.99,101/110)*1.644+(1– min(0.99,101/110)*10 = 2.328
④再次运行,参数 w1 更新为 2.328,则滑动平均值:
w1 滑动平均值=2.956
import tensorflow as tf
#1.定义变量及滑动平均类
#定义一个32位浮点变量,初始值为0,
#这个代码不断更新w1参数,优化w1参数,滑动平均做了一个w1的影子
w1 = tf.Variable(0, dtype=tf.float32)
#定义当前训练轮数,初始值为0,不可被优化(训练)
global_step = tf.Variable(0, trainable=False)
#实例化滑动平均类,给删减率为0.99,当前轮数为global_step
MOVING_AVERAGE_DECAY = 0.99
ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
#ema.apply后的括号里是更新列表,每次运行sess.run(ema_op)时,
#对更新列表中的元素求滑动平均均值
#在实际应用中会使用tf.trainable_variables()自动将所有待训练的参数汇总为列表
ema_op = ema.apply(tf.trainable_variables())
#2. 查看不同迭代中变量取值变化
with tf.Session() as sess:
#初始化
init_op = tf.global_variables_initializer()
sess.run(init_op)
#用ema.average(w1)获取w1滑动平均值(要运行多个节点,作为列表中的元素列出,在sess.run中)
#打印出当前参数w1和w1滑动平均值
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
#参数w1的值赋为1
sess.run(tf.assign(w1, 1))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
#更新step和w1的值,模拟出100轮迭代后,参数w1变为10
sess.run(tf.assign(global_step, 100))
sess.run(tf.assign(w1, 10))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
#每次sess.run会更新一次w1的滑动平均值
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
sess.run(ema_op)
print(sess.run([w1, ema.average(w1)]))
运行结果:
[0.0, 0.0]
[1.0, 0.9]
[10.0, 1.6445453]
[10.0, 2.3281732]
[10.0, 2.955868]
[10.0, 3.532206]
[10.0, 4.061389]
[10.0, 4.547275]
[10.0, 4.9934072]从运行结果可知,最初参数 w1 和滑动平均值都是 0;参数 w1 设定为 1 后,滑动平均值变为 0.9;当迭代轮数更新为 100 轮时,参数 w1 更新为 10 后,滑动平均值变为 1.644。随后每执行一次,参数w1 的滑动平均值都向参数 w1 靠近。可见,滑动平均追随参数的变化而变化。
过拟合:神经网络模型在训练数据集上的准确率较高,在新的数据进行预测或分类时准确率较低,说明模型的泛化能力差。
正则化:在损失函数中给每个参数 w 加上权重,引入模型复杂度指标,从而抑制模型噪声,减小过拟合。
使用正则化后,损失函数 loss 变为两项之和:
loss = loss(y 与 y_) + REGULARIZER*loss(w)
其中,第一项是预测结果与标准答案之间的差距,如之前讲过的交叉熵、均方误差等;第二项是正则化计算结果。
正则化计算方法:
① L1 正则化:
用 Tesnsorflow 函数表示: loss(w) = tf.contrib.layers.l1_regularizer(REGULARIZER)(w)
② L2 正则化:
用 Tesnsorflow 函数表示: loss(w) = tf.contrib.layers.l2_regularizer(REGULARIZER)(w)
用 Tesnsorflow 函数实现正则化:
tf.add_to_collection('losses',
tf.contrib.layers.l2_regularizer(regularizer)(w)
loss = cem + tf.add_n(tf.get_collection('losses'))
例如:
用 300 个符合正态分布的点 X[x0, x1]作为数据集,根据点 X[x0, x1]计算生成标注 Y_,将数据集标注为红色点和蓝色点。
标注规则为:当 x02 + x12 < 2 时,y_=1,标注为红色;当 x02 + x12 ≥2 时,y_=0,标注为蓝色。 我们分别用无正则化和有正则化两种方法,拟合曲线,把红色点和蓝色点分开。在实际分类时,
如果前向传播输出的预测值 y 接近 1 则为红色点概率越大,接近 0 则为蓝色点概率越大,输出的预测值 y 为 0.5 是红蓝点概率分界线。
matplotlib 模块:Python 中的可视化工具模块,实现函数可视化 终端安装指令:sudo pip install matplotlib
函数 plt.scatter():利用指定颜色实现点(x,y)的可视化 plt.scatter (x 坐标, y 坐标, c=”颜色”)
plt.show()
收集规定区域内所有的网格坐标点:
xx, yy = np.mgrid[起:止:步长, 起:止:步长] #找到规定区域以步长为分辨率的行列网格坐标点
grid = np.c_[xx.ravel(), yy.ravel()] #收集规定区域内所有的网格坐标点
plt.contour()函数:告知 x、y 坐标和各点高度,用 levels 指定高度的点描上颜色
plt.contour (x 轴坐标值, y 轴坐标值, 该点的高度, levels=[等高线的高度])
plt.show()
#0. 导入模块,生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
BATCH_SIZE = 30
seed = 2
#基于seed产生随机数
rdm = np.random.RandomState(seed)
#随机数返回300行2列的矩阵,表示300组坐标(x0, x1)作为输入数据集
X = rdm.randn(300, 2)
#从X这个300行2列的矩阵中取出一行,判断,如果两个坐标的平方小于2
#给Y赋值为1,其余赋值为0
#作为输入数据集的标签(正确答案)
Y_ = [int(x0*x0 + x1*x1 < 2) for (x0, x1) in X]
#遍历Y中的每一个元素,1赋值为"red",其余赋值为"blue"
#这样使得显示更加直观
Y_c = [['red' if y else 'blue'] for y in Y_]
#对数据集X和标签Y进行shape整理,第一个元素为-1,表示随第二个元素计算得到
#第二个元素多少列,把X整理为n行2列,把Y整理为n行1列
X = np.vstack(X).reshape(-1, 2)
Y_ = np.vstack(Y_).reshape(-1, 1)
print(X)
print(Y_)
print(Y_c)
#用plt.scatter画出数据集X各行中第0列和第一列元素的点
#用各行Y_c的值表示颜色
plt.scatter(X[:,0], X[:,1], c = np.squeeze(Y_c))
plt.show()
#定义神经网络的输入、参数和输出,定义前向传播过程
def get_weight(shape, regularizer):
w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
return w
def get_bias(shape):
b = tf.Variable(tf.constant(0.01, shape=shape))
return b
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
w1 = get_weight([2, 11], 0.01)
b1 = get_bias([11])
y1 = tf.nn.relu(tf.matmul(x, w1)+b1)
w2 = get_weight([11, 1], 0.01)
b2 = get_bias([1])
y = tf.matmul(y1, w2)+b2; #输出层不过激活
#定义损失函数
loss_mse = tf.reduce_mean(tf.square(y-y_))
loss_total = loss_mse + tf.add_n(tf.get_collection("losses"))
#定义反向传播方法;不含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 100000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 300
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
if i%10000 == 0:
loss_mse_v = sess.run(loss_mse, feed_dict={x:X, y_:Y_})
print("After {} steps, loss is {}".format(i, loss_mse_v))
#xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成二维网络坐标点
xx, yy = np.mgrid[-3:3:0.01, -3:3:0.01]
#将xx, yy拉直,合并成一个2列的矩阵,得到一个网络坐标的集合
grid = np.c_[xx.ravel(), yy.ravel()]
#将网络坐标喂入神经网络,probs为输出
probs = sess.run(y, feed_dict={x:grid})
#probs的shape调整成xx样子
probs = probs.reshape(xx.shape)
print("w1:\n",sess.run(w1))
print("b1:\n",sess.run(b1))
print("w2:\n",sess.run(w2))
plt.scatter(X[:,0], X[:,1], c= np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[0.5])
plt.show()
#定义反向传播方法:包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 100000
for i in range(STEPS):
start = (i*BATCH_SIZE)%300
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
if i%10000 == 0:
loss_v = sess.run(loss_total, feed_dict={x:X, y_:Y_})
print("After {} steps, loss is {}".format(i, loss_v))
xx, yy = np.mgrid[-3:3:0.01, -3:3:0.01]
grid = np.c_[xx.ravel(), yy.ravel()]
probs = sess.run(y, feed_dict={x:grid})
probs = probs.reshape(xx.shape)
print("w1:\n",sess.run(w1))
print("b1:\n",sess.run(b1))
print("w2:\n",sess.run(w2))
print("b2:\n",sess.run(b2))
plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c))
plt.contour(xx, yy, probs, levels=[0.5])
plt.show()
执行代码,效果如下:
首先,数据集实现可视化,x0 + x1 < 2 的点显示红色, x0 + x1 ≥2 的点显示蓝色,如图所示:
接着,执行无正则化的训练过程,把红色的点和蓝色的点分开,生成曲线如下图所示:
最后,执行有正则化的训练过程,把红色的点和蓝色的点分开,生成曲线如下图所示:
对比无正则化与有正则化模型的训练结果,可看出有正则化模型的拟合曲线平滑,模型具有更好的泛化能力。
总结
搭建模块化神经网络八股
前向传播:由输入到输出,搭建完整的网络结构描述前向传播的过程需要定义三个函数:
def forward(x, regularizer): w=
b= y=
return y
第一个函数 forward()完成网络结构的设计,从输入到输出搭建完整的网络结构,实现前向传播过程。该函数中,参数 x 为输入,regularizer 为正则化权重,返回值为预测或分类结果 y。
def get_weight(shape, regularizer):
w = tf.Variable( )
tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
return w
第二个函数 get_weight()对参数 w 设定。该函数中,参数 shape 表示参数 w 的形状,regularizer表示正则化权重,返回值为参数 w。其中,tf.variable()给 w 赋初值,tf.add_to_collection()表示将参数 w 正则化损失加到总损失 losses 中。
def get_bias(shape):
b = tf.Variable( )
return b
第三个函数 get_bias()对参数 b 进行设定。该函数中,参数 shape 表示参数 b 的形状,返回值为参数b。其中,tf.variable()表示给 b 赋初值。
反向传播:训练网络,优化网络参数,提高模型准确性。
def backward( ):
x = tf.placeholder( ) y_ = tf.placeholder( )
y = forward.forward(x, REGULARIZER)
global_step = tf.Variable(0, trainable=False)
loss =
函数 backward()中,placeholder()实现对数据集 x 和标准答案 y_占位,forward.forward()实现前向传播的网络结构,参数 global_step 表示训练轮数,设置为不可训练型参数。
在训练网络模型时,常将正则化、指数衰减学习率和滑动平均这三个方法作为模型优化方法。
在 Tensorflow 中,正则化表示为:首先,计算预测结果与标准答案的损失值
①MSE: y 与 y_的差距(loss_mse) = tf.reduce_mean(tf.square(y-y_))
②交叉熵:ce = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
y 与 y_的差距(cem) = tf.reduce_mean(ce)
③自定义:y 与 y_的差距
其次,总损失值为预测结果与标准答案的损失值加上正则化项
loss = y 与 y_的差距 + tf.add_n(tf.get_collection('losses'))
在 Tensorflow 中,指数衰减学习率表示为: learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE,
global_step,
数据集总样本数 / BATCH_SIZE,
LEARNING_RATE_DECAY,
staircase=True)
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
在 Tensorflow 中,滑动平均表示为:
ema=tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY,
global_step)
ema_op = ema.apply(tf.trainable_variables())
with tf.control_dependencies([train_step, ema_op]):
train_op = tf.no_op(name='train')
其中,滑动平均和指数衰减学习率中的 global_step 为同一个参数。
用 with 结构初始化所有参数
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
for i in range(STEPS):
sess.run(train_step, feed_dict={x: , y_: })
if i % 轮数 == 0:
其中,with 结构用于初始化所有参数信息以及实现调用训练过程,并打印出 loss 值。
判断 python 运行文件是否为主文件 if name ==' main__':
backward()
该部分用来判断 python 运行的文件是否为主文件。若是主文件,则执行 backword()函数。 例如:
用 300 个符合正态分布的点 X[x0, x1]作为数据集,根据点 X[x0, x1]的不同进行标注 Y_,将数据集标注为红色和蓝色。标注规则为:当 x0 + x1 < 2 时,y_=1,点 X 标注为红色;当 x0 + x1 ≥2 时, y_=0,点 X 标注为蓝色。我们加入指数衰减学习率优化效率,加入正则化提高泛化性,并使用模块化设计方法,把红色点和蓝色点分开。
代码总共分为三个模块: 生成数据集(generateds.py) 、前向传播(forward.py) 、反向传播(backward.py)。
①生成数据集的模块(generateds.py)
②前向传播模块(forward.py)
③反向传播模块(backward.py)