深度学习损失函数：交叉熵cross entropy与focal loss
前面
本文主要做两件事情：
1.交叉熵原理
2.引出focal loss原理
其中，交叉熵这里：https://blog.csdn.net/tsyccnh/article/details/79163834
这篇博文写的很详细，很明白，但博士没有总结，我在这里按自己理解重新总结了下，看不太明白的读者建议直接看原文会明白很多。focal的几篇参考：
论文链接：https://arxiv.org/abs/1708.02002
https://blog.csdn.net/u014380165/article/details/77019084
https://blog.csdn.net/dreamer_on_air/article/details/78187565
以下是个人对交叉熵-focal loss的理解汇总，欢迎指正。
一、cross entropy
1 信息量
信息论中有：当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。
注意文中的对数函数的底均为自然数e
2 熵
考虑另一个问题，对于某个事件，有
种可能性，每一种可能性都有一个概率
我们现在有了信息量的定义，而熵用来表示所有信息量的期望，即：
不管单类还是多类图像分类以及目标识别问题，均可以看做0-1分布问题（二项分布的特例），对于这类问题，熵的计算方法可以简化为如下算式：
3 相对熵（KL散度）
相对熵又称KL散度,如果我们对于同一个随机变量 
有两个单独的概率分布 
和
，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。
可以理解为：如果用
来描述目标问题，而不是用
来描述目标问题，得到的信息增量。
在机器学习中，往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。用来表示模型所预测的分布，比如[0.7,0.2,0.1] ，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，等价于。
KL散度的计算公式：
4 交叉熵
由KL散度的计算公式得：
5 应用在深度学习中：
单标签多分类问题：
n是标签类别数
多标签多类分类问题：
多标签多类问题中，每一张图可能会被归为多种标签，每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个类别进行计算，每一个类别只有两种可能值，所以是一个二项分布，每个类别对应的交叉熵公式为：
举例，如一副图片中同时存在青蛙和老鼠，下图是计算结果：
| * | 猫 | 青蛙 | 老鼠 |
|---|---|---|---|
| Label | 0 | 1 | 1 |
| Pred | 0.1 | 0.7 | 0.8 |
例子中的loss计算为：
那么这幅图的loss为（假设数据集只有三个类别）：
另外有分段函数形式的交叉熵函数变体，为了更直观，不妨用来表示predict结果，用
表示gt_label，再引入一个变量
，此时交叉熵可表示为：
对于一个n类的多分类图像问题的一幅图的loss，有：
其中
是该图第
类的预测score，
是该图第类的ground truth，要么是0，要么是1。
个人更喜欢分段函数形式的交叉熵写法，不但写起来简答明了，更重要的是，我们在确定交叉熵公式的时候，不必纠结面对的分类问题是单标签多分类还是多标签单分类，因为分段函数的写法cover了这两种情况。
二、focal loss
focal loss是用来解决困难样本训练问题，以及解决训练样本的imbalance问题。
论文中作者探究one-stage目标检测网络不如rtwo-stage检测网络框架效果好的原因，认为在于one-stage训练的过程中没有two-stage的RPN过程来做proposal，所以会有大量的简单负样本在分类器的训练过程中干扰loss，导致训练模型结果不好。
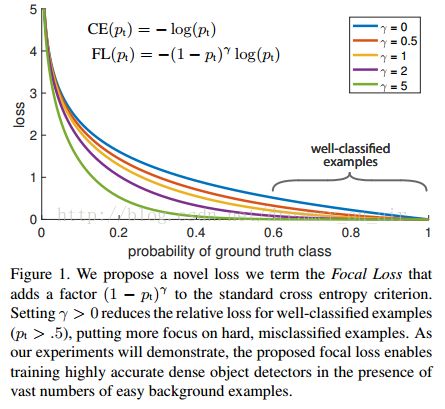
focal loss利用很简单的原理，解决了imbalance，使得目标识别检测AP有几个百分点的提升。其公式是交叉熵损失函数的变种：
可以看到在原有交叉熵loss的基础上增加了一个预测概率
和超参数
，其中的存在就是如果这个样本预测的已经很好了（也就是
接近于1）那么这个样本产生的loss就接近于0，的作用是对这个接近的速度做控制，把loss画出来如下图：
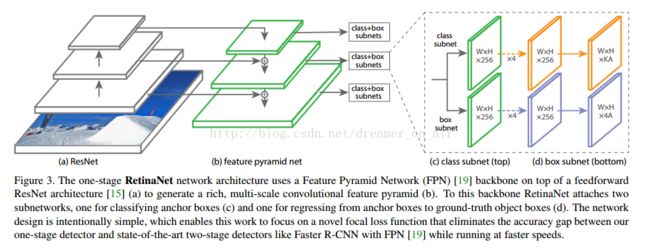
作者因此取了一个很好听的名字RetinaNet，值得一提的是：focal loss初始化的时候加了bias：b = − log((1 − π)/π),其中π = 0.01，用来防止最开始的几轮迭代时梯度不稳定。以下是RetinaNet的基本原理示意图。
作者还增加了平衡权重因子
，解决正负样本不平衡问题，从而有
，
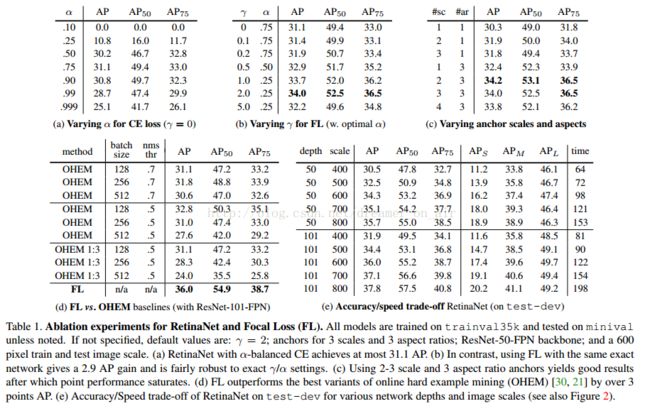
论文实验结果：
