Topic: Binary Search

33. Search in Rotated Sorted Array
这道题我做了不止一次，附上几次的代码：

class Solution {
public:
    int search(vector& nums, int target) 
    {
        int l = 0, r = nums.size();
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] >= nums[l])
            {
                if (target >= nums[l] && target < nums[mid]) r = mid;
                else l = mid + 1;
            }
            else
            {
                if (target <= nums[r-1] && target > nums[mid]) l = mid + 1;
                else r = mid;
            }
        }
        return -1;
    }
};

（2）这是最近一次做的，现在觉得比较intuitive：

首先我们知道，target这个值要么找不到，要么就是在0~nums.size()-1之间。所以r=nums.size()-1。经过以下循环后，l和r将收敛于一个index，这个index的值未被比较过，所以要判断是否等于target。因为我们update r的条件和r的初始值的设置，此index肯定不会out of bound。Edge case：nums为空，此时进行nums[l]操作时要先行判断。

class Solution {
public:
    int search(vector& nums, int target) 
    {
        if (nums.empty()) return -1;
        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target) return mid;
            else if (nums[mid] >= nums[l])
            {
                if (target >= nums[l] && target < nums[mid]) r = mid - 1;
                else l = mid + 1;
            }
            else 
            {
                if (target > nums[mid] && target <= nums[r]) l = mid + 1;
                else r = mid - 1;
            }
        }
        return nums[l] == target ? l : -1;
    }
};

（3）不好意思又做了一遍，这次是这样的

class Solution {
public:
    int search(vector& nums, int target) 
    {
        int l = 0, r = nums.size();
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target) return mid;
            if (nums[mid] == nums[l]) l++;
            else if (nums[mid] > nums[l])
            {
                if (target >= nums[l] && target < nums[mid]) r = mid;
                else l = mid + 1;
            }
            else
            {
                if (target <= nums[r-1] && target > nums[mid]) l = mid + 1;
                else r = mid;
            }
        }
        return -1;
    }
};

这个代码跟81. Search in Rotated Sorted Array II是一毛一样的！原谅我做了这么多遍才发现能有这个操作。。。因为array里只有两个数的时候，有可能l和mid相等。

81. Search in Rotated Sorted Array II
这道题如果遇到2201222这样的情况就无法根据nums[mid] >= nums[l]来判断inorder区间了，我们要将l往右移再进行判断直到nums[mid] > nums[i]。由于我们在前面已经判断了nums[mid] == target而不符合，可以放心地相信target和nums[mid]不一致，放心地移。

那下一个判断会不会出现nums[mid] == nums[r-1]的情况，答案是不可能。如果右边是排序好的，那么左边也一定是排序好的（重合元素已被排除），所以不可能到这个if。如果右边是乱序的，那左边就是排序好的，肯定也去了上一个if。

class Solution {
public:
    bool search(vector& nums, int target) 
    {
        int l = 0, r = nums.size();
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target) return true;
            else if (nums[mid] == nums[l]) l++;
            else if (nums[mid] > nums[l])
            {
                if (target >= nums[l] && target < nums[mid]) r = mid;
                else l = mid + 1;
            }
            else
            {
                if (target > nums[mid] && target <= nums[r-1]) l = mid + 1;
                else r = mid;
            }
        }
        return false;
    }
};

153. Find Minimum in Rotated Sorted Array
这道题我们为了找规律可以先列出一些例子：
0 1 2 3 4 5 6 7
7 0 1 2 3 4 5 6
6 7 0 1 2 3 4 5
5 6 7 0 1 2 3 4
4 5 6 7 0 1 2 3
3 4 5 6 7 0 1 2
2 3 4 5 6 7 0 1
1 2 3 4 5 6 7 0
观察发现，若中间项（标粗）与最右边项相比，中<右，那么右边肯定是升序的，因此我们二分法往左走，同时要把中间这项保留（5 6 7 0 1 2 3 4）。若中>右，说明右边包含最小值，往右走，同时不用把中间项保留。

34. Search for a Range
做这种题首先判断所找的元素在array里吗，然后列出一些例子来检验。一般包括>3个元素的例子，然后2个元素的例子，1个元素的例子，0个元素的例子。

这道题要找的元素不一定在array里，所以用size表示右边界。
（1）找左边界：要注意l==r了以后，我们找到的也不一定是target，比如[10]找5这个例子。所以要判断nums[l]==target是否成立。但是我们在index的时候要注意nums[l]有可能是out of bound了哦。如果out of bound说明元素肯定没找到，不然l和r是会汇合的。
（2）找右边界：因为我们在往右挪的同时也要保持记录此刻的数，所以每次都要更新一下end。我们可以保证不用查其它情况，比如l会不会go out of bound，不可能，因为通过（1）我们知道target肯定存在。

再比如会不会我们找到的end不是真正的end，最后真正的end没有找到。不可能，唯一这样可能出现的情况是，在r-l==1的时候，nums[l]==target, nums[r]==target，再l=mid+1的时候，我的l和r就会重合，但是我还有一个最后的end就被漏掉了。但这种情况是不可能的，因为我们维护的右边界的值肯定不是target。右边界值是target的情况有两种，一种是一开始就是target，那不可能因为我们一开始是nums.size()，第二种是当target==nums[mid]的时候，我们不会移动r，而是移动l，所以说我们维护的右边界的值肯定不是target。所以在r-l==1的时候，nums[l]==target，我们再l=mid+1的时候，l和r重合的时候，end就已经找到了。

class Solution {
public:
    vector searchRange(vector& nums, int target) 
    {
        int l = 0, r = nums.size();
        int begin = -1;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if (l == nums.size() || nums[l] != target) return {-1, -1};
        else begin = l;
        
        l = 0, r = nums.size();
        int end;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (nums[mid] == target)
            {
                end = mid;
                l = mid + 1;
            }
            else if (nums[mid] < target) l = mid + 1;
            else r = mid;
        }
        return {begin, end};
    }
};

278. First Bad Version
由于bad version一定在array里，当我们找到一个bad version的时候，我们要往左看看有没有更早出现的，这时候我们要包括mid这个边界作为右边界，因为这样可以保证两个指针重合的时候，所返回的一定是一个bad version。如果我们找到的不是bad version，那valid的一定在右边。

这道题如果有follow up可以问如果array里有duplicates怎么办，如果不一定有个bad version怎么办。后者可以通过l是不是null ptr来看有没有bad version，而更新条件呢是一样的，r=mid。因为我们要保证说两个重合的时候，返回的l一定是个bad version。

// Forward declaration of isBadVersion API.
bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) 
    {
        int l = 1, r = n;
        while (l < r)
        {
            int mid = l + (r - l) / 2;
            if (isBadVersion(mid)) r = mid; // bad version in the left, including the boundary
            else l = mid + 1;
        }
        return l;
    }
};

4. Median of Two Sorted Arrays
这道题用getKthElement来做最方便，奇偶性的区分只要调用两次函数即可。getKthElement有很多做法：
（1）用two pointer做，O（k）
（2）logm+logn：找出两个array中点，若俩中点的index相加小于k，说明k肯定不在更小的array[mid]的左边。若俩中点的index相加大于k，说明k肯定不在更大的array[mid]的右边。

这种解法的代码：

（3）logk：这种方法很容易理解，但是写起来在index manipulation中需要注意非常多的edge case。在两个array中找出第k/2个元素，并进行比较。代码：

class Solution {
private:
    double findNth(int n, vector& nums1, vector& nums2, int l1, int r1, int l2, int r2)
    {
        // ensures the size of arr1 < the size of arr2
        if (r1 - l1 > r2 - l2) return findNth(n, nums2, nums1, l2, r2, l1, r1);
        // if arr1 is empty
        if (l1 > r1) return nums2[l2 + n - 1];
        // a base case
        if (n == 1) return min(nums1[l1], nums2[l2]);
        
        // r1 - l1 is the last element of the array
        // n / 2 means there are n / 2 elements in the left subarray 
        int halfN1 = min(r1 - l1 + 1, n / 2), halfN2 = min(r2 - l2 + 1, n / 2);
        // we want to -1 because want to compare the kth element
        if (nums1[l1+halfN1-1] > nums2[l2+halfN2-1])
        {
            // n - halfN2 because we can be sure that halfN2 elements are certainly in the left of the kth elements
            // we have deleted the interval [l2, halfN2]
            return findNth(n - halfN2, nums1, nums2, l1, min(l1 + halfN1, r1), l2 + halfN2, r2);
        }
        return findNth(n - halfN1, nums1, nums2, l1 + halfN1, r1, l2, min(l2 + halfN2, r2));
    }
    
public:
    double findMedianSortedArrays(vector& nums1, vector& nums2) 
    {
        if (nums1.empty() && nums2.empty()) return 0;
        int ele = nums1.size() + nums2.size();

        // odd: 9, then the 5th largest & 5th largest
        // even: 10, then the 5th largest & 6th largest
        int m1 = ele / 2 + 1, m2 = (ele - 1) / 2 + 1;
        double mid1 = findNth(m1, nums1, nums2, 0, nums1.size() - 1, 0, nums2.size() - 1);
        if (m1 == m2) return mid1;
        double mid2 = findNth(m2, nums1, nums2, 0, nums1.size() - 1, 0, nums2.size() - 1);
        return (mid1 + mid2) / 2;
    }
};

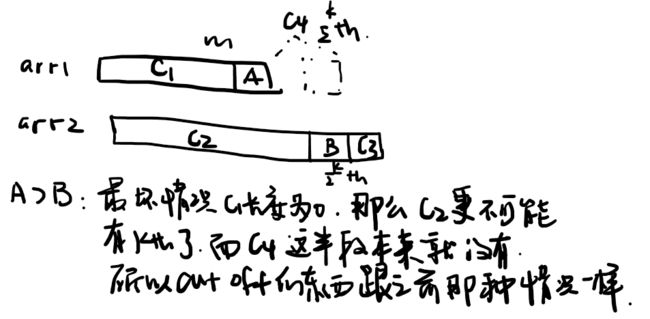
首先了解big picture：

Edge case/细节处理：
（1）我们在trim elements的时候要不要把第k/2个元素也trim掉？如果A>B的话，A是有可能是第K个元素的，所以我们要保留A。但B不可能是第K个元素，所以我们要去除B。
（2）arr1和arr2的长度是有可能小于k/2的，也就是说k/2这个index可能会out of bound。这时候我们就要取一下min。图例是arr1的k/2 out of bound的情况。

（3）因为k/2有可能是除不尽的，比如k=3的情况，k/2=1，如图示我们假设第一个1小于第二个1（共享一段代码，即我们只分if (nums1[l1+halfN1-1] > nums2[l2+halfN2-1])和if (nums1[l1+halfN1-1] <= nums2[l2+halfN2-1])两种情况来讨论）。

（4）根据（3）进行代码调整。调整前为l1 + halfN1 - 1，而由于我们想保留右半段多一个元素，改成l1 + halfN1，但这时候可能出现l1 + halfN1out of bound的情况，比如：[2], [1,3,4]，进行update的时候我们发现第一个array出现了index为1的情况，这显然是不允许的，因此我们取一遍min(l1 + halfN1, r1)。

时间复杂度上，由于k<=m+n，而我们每次trim都把必然不是kth smallest element的k/2个元素给trim掉了，所以时间为logk=log(m+n)。

这道题的edge case……真的是要多写一些test case然后有针对性地调整代码。第三个第四个edge case是比较难发现的。

50. Pow(x, n)
思路一：首先对n进行edge case的处理。然后用二分法递归来做，分奇数偶数两种情况讨论。时间O（logn），空间O（logn）。
思路二：根据power的规律，把非2次数的数转化为2的次数的数来做。比如13=1101，看到1我们就把数乘到result里去，否则就只乘x。原因如图示。

时间也是O（logn），因为我们把n>>=1执行了logn次。空间O（1）。

Edge case：
（1）n=0时，return 1；
（2）n为负数时，x=1/x，n = -n；
（3）n为INT_MIN时，-n会out of bound。所以我们先把n转换成long long再做。
（4）n转换成long long之后，记得要用转换后的nLong来进行比较，不要用之前的n了（很容易出粗心的bug）

29. Divide Two Integers
对input的error checking和处理：
（1）若divisor = 0
（2）若divisor = -1而dividend=INT_MIN，造成overflow
（3）判断符号
（4）由于之后的操作要进行位移，把int转换成long long来做，并取绝对值

思想方法就是用dividend一直减去divisor。由于我们追求类似logn的复杂度，需要进行bit shift，所以每次将divisor进行bit shift，当大于dividend时再开始第二轮。这么一来的时间复杂度，内循环为logn，外循环：我们获得的divisor一定是>n/2了，不然我们还能继续除（copy <<= 1无非就是乘以2的意思）。所以每一次的外循环都能使n减半，也就是说外循环也运行logn次。所以时间复杂度是O（（logn）^2）。空间复杂度O（1）。

class Solution {
public:
    int divide(int dividend, int divisor) 
    {
        if (!divisor) return INT_MAX;
        if (dividend == INT_MIN && divisor == -1) return INT_MAX;
        int sign = ((dividend > 0) ^ (divisor > 0)) == 1 ? -1 : 1;
        
        long long d = llabs(dividend);
        long long s = llabs(divisor);
        int res = 0;
        while (d >= s)
        {
            long long copy = s;
            int temp = 1;
            while (d >= copy << 1)
            {
                copy <<= 1;
                temp <<= 1;
            }
            res += temp;
            d -= copy;
        }
        return sign * res;
    }
};

287. Find the Duplicate Number
这道题挺灵活的考察了二分法和two pointer。

思路一：二分法。以前的二分一般是对sum array进行二分查找。这次怎么说呢？我们取1~n的中间数mid并且数有多少个元素比mid小。如果说>size/2的话，说明重复的元素在mid以下，不然的话在mid及以上。每次数要O（n）时间，一共数logn次，所以时间是nlogn。

思路二：fast slow pointer。这种有n+1个数而index是1~n的，多半可以用index之间的关系来做。我们要想出一种办法来检验index重复到达。光这么想就只能想到hashmap。但实际上这个问题等价于查圈是不是，就是一个node到了不只一次。因此我们用fast slow pointer，与linked list查圈类似。O（n）即可。

240. Search a 2D Matrix II
很棒的一道题，严格意义上不算是“二分法”，有很巧妙的insight。matrix是从左到右，从上到下sorted的，我们能得出的最直观信息是矩阵右下角的数值最大，那么如果target比这个数大，就返回false。然后从这个思路，就得不到什么信息了。

换一种思路，对于第一行最后一列来说，如果target比这个值大，那么我们只要看下一行开始的就行了，因为右边没有列了。如果target比这个值小，那么我们只要看以上一列为结尾的就行了，因为上面没有行了。如果target等于这个值，就return true。

时间：O（m+n），空间：O（1）。

222. Count Complete Tree Nodes
思路一：一直往左走算出左子树最深，一直往右走算出右子树最右枝深度。若两者相等，则返回总节点数，若两者不相等，则再往左、往右递归。这样的时间：对于每个node算高度是nlogn，每次把问题一分为二，两个subproblem都要照顾到，遍历的节点数总共为n个，时间是O（nlogn）。

思路二：左子树算出深度（一直往左走），右子树算出深度（右子树也一直往左走）。若两者相等，知道左子树的complete的。若两者不等，知道右子树是complete的。因此我们可以算出complete的那个子树的nodes，然后递归另一个子树的nodes。这样一来，每次把问题一分为二，但只要递归一个subproblem，也就是说每次把问题减半了，我们所要遍历的node一共是logn个，每次求高度是logn，所以时间复杂度为O（logn）^2。

378. Kth Smallest Element in a Sorted Matrix
思路一：用range做bs，左是第一个（左上）矩阵元素，右是最后一个（右下）。根据“是否有k个元素小于mid”这个条件不断逼近直到左右相遇，就能得到我们求的第k大元素。

再详述一下，我们要求的是<=mid的值有k个，那么mid就是第k小的数。我们在算个数的时候，用的是upper_bound这个函数，也就是说会把所有跟mid一样的数都给数进去。那么数完以后，count值必然要>=k才行，不然也就是说<=mid的值

第二种情况，cnt>k，也就是说<=mid的值>k个。比如[1,2,3,3,3,5]，k=4，mid=3，count=5，满足cnt>k。这时候我们可以发现，第k大的数其实已经被找到了。再比如[1,2,2,2,2,5]，k=4，mid=3，count=5，满足cnt>k，但是我们要找的数是2，而不是mid=3，所以第k大的数还没有被找到。综合上述两种情况，当cnt>k时，我们的solution<=mid，因此我们使得r=mid。

第三种情况，cnt=k，也就是说<=k的值=k个。这时候也要分mid的值在矩阵中和不在矩阵中两种情况。比如[1,2,3,3,5]，k=4，mid=3，count=4，满足cnt=k，第k大的数就是mid=3。再比如[1,2,2,2,5]，k=4，mid=3，count=4，满足cnt=k，但第k大的数还没找到因为mid=3但我们要找的是2。因此我们也使得r=mid。

第一种情况可以说是“排除不可能”，第二、第三两种是“保持可能”。根据上述三种情况的分类讨论，我们保持着left<=solution<=right这个invariant。当循环终止，由于left==right，我们便得到了solution=left。那么现在的关键点就在于，如何证明最终相遇时的left和right存在在矩阵中，因为我们用mid=left+(right-left)/2的时候，mid是不一定在矩阵中的。

我们要确定的是，solution肯定是在矩阵中的，而l和r的作用无非在于越来越靠近solution。l和r可能在某一点可能是不在矩阵中的数，但是当l=r=solution的时候，就会在矩阵中，因为solution在矩阵中。这里我们想证明的是l最终在矩阵中，但因为l=solution而solution在矩阵中，我们可以把问题转化为了证明solution最终在矩阵中。而by definition，solution就是在矩阵中的。

时间：log(max-min)*nlogn（对一个nxn的矩阵）。

思路二：总的思路与思路一一样，但是在寻找小于mid的数的时候我们可以做到O（n）的复杂度。因为column也是sorted的，我们可以用“贪吃蛇”的方法来做。

思路三：参见评论区的O（#row）做法，以后再细看。

35. Search Insert Position
这道题是找lower_bound，自己写的时候注意，由于我们可能找到nums array之外去，r=nums.size()而不是size()-1，最后返回的是r。

74. Search a 2D Matrix
转换为一个array做。注意，由于元素可能不被找到，我们使得r=nums.size()，这样当l与r重合的时候，我们能保证每一个矩阵中可能的元素都是被遍历到的。尤其是比矩阵中的最大值还大的时候，如果用nums.size()-1，r-l=1的时候，如果元素不是矩阵中的最后一个元素，我们可以保证r被检查过，因为r从r=mid来。如果元素是矩阵中的最后一个元素，我们不能保证r被检查过。

162. Find Peak Element
这题是376作业里的一道bs。找local max/min。

367. Valid Perfect Square
l<=r的时候，我们要让l=mid+1,r=mid-1。另外注意

475. Heaters
将heaters array sort，然后对每间房屋，在heaters array里进行bs，分别与最近的左和右heater比较。由于只要有一个heater房屋就能热，我们取两者左右距离的最小值，而每次对result都进行max操作。注意lower_bound out of bound的情况。

441. Arranging Coins
采取l<=r, r=mid-1, l=mid+1的条件。注意overflow。

270. Closest Binary Search Tree Value
思想方法很简单，但是test case……我觉得这么无聊的test case不是很有必要吧，各种overflow什么的。

658. Find K Closest Elements
思路一：用bs先找到closest然后用双指针做。注意closest的candidate指针要一直跟。

思路二：定义comparator直接sort。

class Solution {
public:
    vector findClosestElements(vector& arr, int k, int x) 
    {
        sort(arr.begin(), arr.end(), [x](int a, int b) { return abs(a - x) == abs(b - x) ? a < b : abs(a - x) < abs(b - x); });
        vector res(arr.begin(), arr.begin() + k);
        sort(res.begin(), res.end());
        return res;
    }
};

230. Kth Smallest Element in a BST
inorder traverse中，每次一个节点的左节点遍历完之后增加count，当count==k时将value记下。由于我们一直在增加count，我们可以利用count的值来判断是否应该终止寻找而返回。

436. Find Right Interval
思路一：建立两个map，一个start和一个end array，一个result array，进行bs。
思路二：只sort interval，然后直接bs。这里注意因为map以vector作为key的话要自己来定义hash function，所以可以用map来做，在map中进行bs。

class Solution {
public:
    vector findRightInterval(vector& intervals) 
    {
        vector res(intervals.size());
        map m;
        for (int i = 0; i < intervals.size(); ++i) m[intervals[i].start] = i;
        for (auto &item: m)
        {
            int end = intervals[item.second].end;
            auto ptr = m.lower_bound(end);
            res[item.second] = ptr == m.end() ? -1 : ptr->second;
        }
        return res;
    }
};

思路三：将end和start的vector排序之后发现，由于end是升序的，那么这一个end如果在start中找不到比这个end更大的start，下一个end更找不到。因此我们只要遍历一遍end，每次遍历的时候，从上次结束的地方开始遍历start即可。这个方法是最巧妙的。

454. 4Sum II
这题用hashtable的思路更好吧。bs只不过用vector替代了hashmap，寻找的方式不一样而已，基本思路都是一样的。

300. Longest Increasing Subsequence
这题用DP很明显O（n^2）。用bs很巧妙。我们维护一个一直是排序好的array，每一次新进来一个元素，在这个array里找这个元素，如果这个元素比array里的所有元素都大，就append到array尾，反之就用lower_bound找到这个元素应该被插入的位置（lower_bound因为我们需要的是strictly increasing subsequence）。最后得到的subsequence长度就是结果，但是里面的值不一定是结果哦。

392. Is Subsequence
这题还蛮适合当一面面试题的，先考察会不会做，然后考察能不能优化。当有两个array/list/string，一个比较大，另一个比较小，十有八九要遍历小的，在大的那个里面做bs。那问题是现在t里的字母不是排序好的，我们怎么来做bs呢？

关于“全是英语小写字母”的问题，我们常会建立一个长度为26的char array。我们将t中所有字母的index都保存在这个array（vector>）中，注意这个array中的每个entry都是排序好的，因为我们是按t的index在遍历。最后遍历一遍s，对每个char在array中寻找entry，如果entry为空，或者entry中的index没有比上一个有效index（记为prev）更大的index了，就返回false，否则遍历完s就返回true。

69. Sqrt(x)
167. Two Sum II - Input array is sorted
374. Guess Number Higher or Lower
350. Intersection of Two Arrays II
278. First Bad Version
35. Search Insert Position - lower_bound
很明显的二分法

感谢以下作答：

“因为使用mid = (L+R)/2这种计算方式的话，当R-L=1时，mid是等于L的。而此时如果恰好执行了L=mid，那就意味着在这次iteration中，L的值没有变化，即搜索范围没有变，于是就死循环了。

至于R的取值方式不同，更多地是反映出实现者的思路不同：如果取成nums.size()，则可能意味着你认为目标可能出现在[L, R)中；hi取成nums.size()-1，意味着你认为目标一定会出现在[L, R]中。持前种思路的人，r = mid会更自然，而持后一种思路的人，则更可能会写r=mid-1 (当然他写成r = mid也是一样可以的)。

一个有助于你快速判断是否会死循环的方法，是考虑R-L=1的情况。在这种情况下target可能有小于，等于A[L], 小于，等于，大于A[R]共5种情况。快速验证一下这五种情况是否都能正常退出并返回正确值即可。”——from stellari。”

Topic: Binary Search

感谢以下作答：

你可能感兴趣的:(Topic: Binary Search)