问题提出
一个集合中有N个点,N个点中有许多的相连的,任意给出两个点,如何才能快速地知道这两个点是否是相连(间接相连也算)的 ? 如果不相连,如何才能快速高效地实现连接?这样的问题在计算机网络的连接和电子电路中都有出现。
设计API
为了说明问题,我们设计了一份API来封装所需要的基本操作:初始化整个集合,连接两个点,判断包含两个点的一条连接链,判断两个点是否相连,返回链的数量。
//public class UF
// UF(int N) 初始化整个集合
// void union(int p, int q) 在p,q之间添加一条连接
// int find(int p) p所在的链的标识符
// boolean connected(int p, int q) 如果p和q存在于同一条链之中则返回true
// int count() 统计集合中链的数量
//
当初始化所有的点组成的集合的时候,用1~N-1来表示所有的点。如果两个点在不同的链当中,可以用union来将两条链连接,find方法用来返回某个点所在的连通链的标识符,connected用来判断两个点是否相连(即是否在一条链上),count方法用来返回整个集合当中链的条数。
在我们的实现当中,我们将使用一个大小为N的数组来表示N个点,数组的index即是每一个点的名称,每个index下存储的东西就是该点所属链的标识符。
最初版本的实现-quick find
import java.util.Scanner;
public class UF {
private int[] id; //分量id,以触点作为索引
private int count; //分量数量
public UF(int N){
count = N;
id = new int[N];
for (int i = 0;i < N;i++){
id[i] = i;
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int find(int p){
return id[p];
}
public void union(int p , int q){
//将p和q所属的分量归并(连接两条链)
int pID = find(p);
int qID = find(q);
//如果p和q已经在相同的分量当中则不需要采取任何行动
if (pID==qID) return;
for (int i = 0; i < id.length; i++){
if (id[i] == pID) id[i] = qID;
}
count--;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
System.out.println("Input the length of array!");
int N = sc.nextInt();
UF uf = new UF(N);
while (sc.hasNext()){
int p = sc.nextInt();
int q = sc.nextInt();
if (uf.connected(p,q)) continue;
uf.union(p,q);
System.out.println(p+""+q);
}
System.out.println(uf.count + "components");
}
}
这一实现方案在检查两个点是否连接是效率非常的高,然而在连接两条链是效率却十分低下。例如p所在的分量的标识符为1,q所在的分量的标识符为2,当想把p和q所在的分量归并的时候,就需要遍历整个数组,将所有标识符为1的索引里的标识符改为2。这样就导致当我们将N个点全部连通的时候,调用了union方法N-1次,union方法里面又一个循环,这就相当于是两个循环,所以这个算法的运行时间对于得到少量连通分量的应用来说是平方级别的。当使用100万个点和200万条连接的时候,这个算法运行了几十分钟。
第一次改进后的实现-quick union
import java.util.Scanner;
public class UF {
private int[] id; //分量id,以触电作为索引
private int count; //分量数量
public UF(int N){
count = N;
id = new int[N];
for (int i = 0;i < N;i++){
id[i] = i;
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int find(int p){
while (p != id[p]) p = id[p];
return p;
}
public void union(int p , int q){
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
id[pRoot] = qRoot;
count--;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
System.out.println("Input the length of array!");
int N = sc.nextInt();
UF uf = new UF(N);
while (sc.hasNext()){
int p = sc.nextInt();
int q = sc.nextInt();
if (uf.connected(p,q)) continue;
uf.union(p,q);
System.out.println(p+""+q);
}
System.out.println(uf.count + "components");
}
}
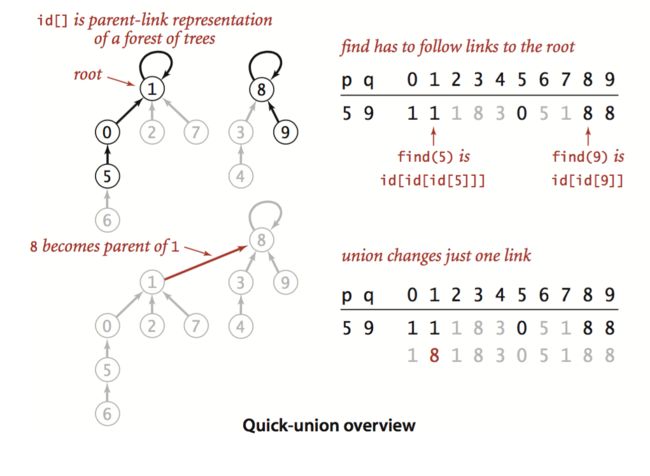
这一次的改进主要是为了加快union算法的速度。这一次我们不是使用一条链上的点用同一个标识符的方式,而是使用类似于链表的方式,比如点1和点2相连,就在索引2里面放置值1,而独立的一个点则索引和里面放置的值都是索引值。在这个算法里面,find方法显然比上面要慢一些,确定任意两个点是否连通的方式是分别由两个点的索引里面所存的下一个节点的索引一路上溯到它们所在的链的根节点,如果是同一个根节点,那么就是连通的,否则就不连通,如果想要他们连通,就使用改良后的union方法将两个根节点连接起来--由其中一个根节点的索引中存储另一个根节点的索引值。然而这种改良在很多情况下并没有比未改良的方法快(简单分析和实践都已经证明),而且在一种特殊的输入下:01,12,23,34,45,……这个链会变成一条超长的链表,而不是树的形状,这样就和未改进没有区别,依然类似于遍历数组。
第二次改进后的实现-加权quick-union算法
幸运的是,我们只需要稍微改变一下上面的算法,就能保证上面的问题不再出现。
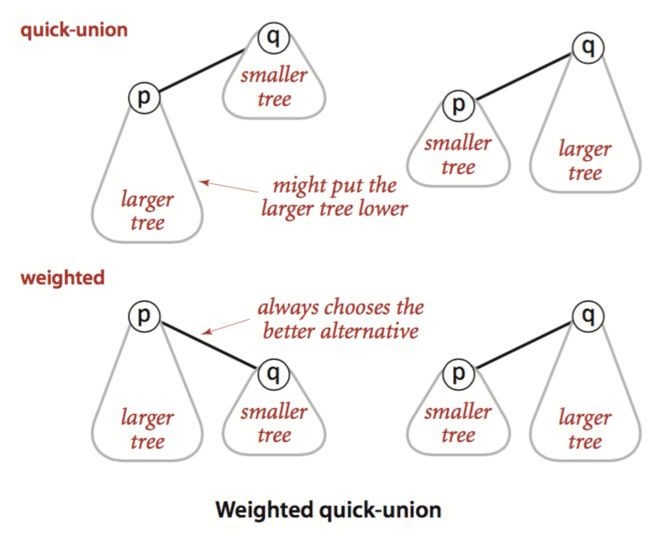
与其胡乱的将一棵树连接到另一棵树,我们更应该总是将一棵较小的树添加到一棵较大的树上,这样我们就能够限制树的高度,从而保证查找的时间复杂度为lgN。
import java.util.Scanner;
public class UF {
private int[] id; //分量id,以触点作为索引
private int[] size; //由触电索引的各个节点所对应的分量的大小
private int count; //分量数量
public UF(int N){
count = N;
id = new int[N];
for (int i = 0;i < N;i++){
id[i] = i;
}
size = new int[N];
for (int i = 0;i < N;i++){
size[i] = 1;
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int find(int p){
while (p != id[p]) p = id[p];
return p;
}
public void union(int p , int q){
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
if (size[pRoot] < size[qRoot]){
id[pRoot] = id[qRoot];
size[qRoot] += size[pRoot];
}else {
id[qRoot] = id[pRoot];
size[pRoot] += size[qRoot];
}
count--;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
System.out.println("Input the length of array!");
int N = sc.nextInt();
UF uf = new UF(N);
while (sc.hasNext()){
int p = sc.nextInt();
int q = sc.nextInt();
if (uf.connected(p,q)) continue;
uf.union(p,q);
System.out.println(p+""+q);
}
System.out.println(uf.count + "components");
}
}
这样就能保证在将N个节点完全连接起来的时候的时间复杂度为NlgN,这样的时间复杂度已经复合解决很多大型问题的要求。
最优算法-路径压缩的加权quick-union算法
在理想情况下,我们都希望所有的节点都直接连接在它的根节点上,这样就只需一次操作就能找到其根节点,能表现出常数时间,这种方法被称为路径压缩方法。
public int find(int p){
int temp = p;
while (p != id[p]) p = id[p];
id[temp] = id[p];
return p;
}
将find方法如此修改就可以实现路径压缩。
此时quick-union算法的速度已经比一开始的时候快了很多很多。
资源以及参考
本笔记是学习普林斯顿大学算法课程以及阅读其教材《算法》第四版所作
用于跑着玩的拥有100万个点和200万条链接的文件(直接下载链接文件即可)
http://algs4.cs.princeton.edu/15uf/largeUF.txt
命令行运行:
cd到.java文件所在文件夹,执行一下命令,如果.java文件中含有包名,注意将其删除
% javac UF.java
% java UF < largeUF.txt