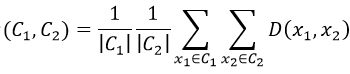一些聚类算法
Birch层次聚类 ,KMeans原形算法 ,AGNES层次算法, DBSCAN密度算法, LVQ原形算法
简单做一个个人想法记录,其实聚类算法来说大体上的思路都非常简单,无非是找点或者区域,计算它们之间的距离(这个距离为抽象意义上的距离,不同的内容有不同的距离表示方式),然后根据一定规则(一般都是以最近为相邻),然后叠加在一起。
简单来说:聚类就是如何确认某些点或区域,再根据这些选好的点与区域再进行距离计算,从而进行划分。
简单代码可见:https://github.com/AresAnt/ML-DL
Kmeans算法:(原形聚类方法)
最简单的Kmeans算法的思路,首先我们要确定划分几个类(即K值)。
假设这里需要划分3个类:
- 先初始化三个随机样本点。(随机点一定是要在样本范围之内,一般来说可以以随机挑选三个样本点作为起始样本点)
- 对全样本进行遍历,与三个随机点进行计算,与哪个随机点近就划分进入哪个随机点的区域内。
- 一次划分完毕后,对区域内所有的点间距离进行平均计算。假设当前区域内划分进来了m-1个样本点,加上随机点,总共为m个样本在这片区域内。两两计算它们之间的距离,总共需要循环计算 m (m-1) 次,然后除以这片区域内的样本数量。即
$$ {\frac{1}{m}}{\sum^{m}_{i=1,i- 算出后的点,即为新的随机样本点(也称为算质心),然后重复以上的过程,不断的更替质心直到最后确定。
LVQ算法:(原形聚类方法)
LVQ算法是假设数据样本带有类别标记的,学习过程中利用样本的这些监督信息来辅助聚类。
(简单描述,其实它的做法与KMeans类似,也是相当于是一个找质心点的过程,这里为找原形向量,每一行的向量其实对应的就是上述所提到的质心点)
算法流程:
输入:样本集D = {(x1,y1),(x2,y2),....,(xm,ym)} (设 D1 = (x1,y1))
原形向量的个数q,各原形向量的类别标记 { t1,t2,t3,t4,..,tq } 【这个划分的意思是指,假设我上述样本集中的 yi 为两类,即 0,1, 那么我可以设置原形向量的类别为 { 1,1,0,0,1} (意思为1分类的样本最后会划分为3个簇,0分类的样本最后会划分为2个簇】
学习率 α (0~1)
过程:
- 初始化一组原形向量 P = {(p1,t1),(p2,t2) ,...,(pq,tq)} (这个初始化一般以随机改 ti
分类下的样本作为 pi)
# 初始化原形向量,这里做简单操作,假设希望找到 3个好瓜的簇,2个坏瓜的簇,总共五个簇
good = np.where(rowdata_y == 1)[0]
bad = np.where(rowdata_y == 0)[0]
vectorlist = random.sample(list(good),3) + random.sample(list(bad),2)
P_x = np.zeros((k,rowdata_x.shape[1]))
P_y = np.zeros((k,rowdata_y.shape[1]))
for i in range(len(vectorlist)):
P_x[i] = rowdata_x[vectorlist[i]]
P_y[i] = rowdata_y[vectorlist[i]]
- 循环迭代:
从样本 D 中随机抽取一个样本(xi,yi)进行向量校正(类似前面的移动质心点)
找出最小的原形向量 pj
if D.yi == P.tj:
P.pj = P.pj + α * ( D.xi - P.pj )
else:
P.pj = P.pj - α * ( D.xi - P.pj )
- 输出原形向量 P
缺点:LVQ算法的质心点移动取决于进来计算的随机点,这个点的进来顺序有关,如果进来的点都过于的奇特,那么质心点的改变也会特别的奇怪。需要一定量的迭代次数来进行更正。不过因为随机点是随机产生,随机产生符合正太分布,正态分布的点数为样本中心点质量有关。
AGNES 层次聚类算法:(层次聚类算法)
层次聚类算法可以有“自底向上”的聚合策略,也可以采用“自顶向下”的分拆策略。(2分-Kmeans就是“自顶向下”的策略)
AGNES是“自底向上”的聚合策略,它简单的先将每个样本点看做是一个簇,然后通过计算相应的距离,选取最小的两个簇合成为以个簇,以此反复,计算量庞大。
算法思路,对于数据集D,D={x_1,x_2,…,x_n}:
将数据集中的每个对象生成一个簇,得到簇列表C,C={c_1,c_2,…,c_n}
a) 每个簇只包含一个数据对象:c_i={x_i};
重复如下步骤,直到C中只有一个簇:
a) 从C中的簇中找到两个“距离”最近的两个簇:min〖D(c_i,c_j)〗;
b) 合并簇c_i和cj,形成新的簇c(i+j);
c) 从C中删除簇c_i和cj,添加簇c(i+j)
稍微注意一下簇间距离运算的方式:
在上面描述的算法中涉及到计算两个簇之间的距离,对于簇C_1和C_2,计算〖D(C_1,C〗_2),有以下几种计算方式:
单连锁(Single link):
两个簇之间最近的两个点的距离作为簇之间的距离,该方式的缺陷是受噪点影响大,容易产生长条状的簇。
全连锁(Complete link)
两个簇之间最远的两个点的距离作为簇之间的距离,采用该距离计算方式得到的聚类比较紧凑。
平均连锁(Average link)
两个簇之间两两点之间距离的平均值,该方式可以有效地排除噪点的影响。
Birch层次聚类算法:(层次聚类算法)
不做多余赘述,可以查看该链接:http://www.jianshu.com/p/e0c4f19f7ab1
DBSCAN密度聚类算法:(密度聚类算法)
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
该算法利用基于密度的聚类的概念,即要求聚类空间中的一定区域内所包含对象(点或其他空间对象)的数目不小于某一给定阈值。DBSCAN算法的显著优点是聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类。但是由于它直接对整个数据库进行操作且进行聚类时使用了一个全局性的表征密度的参数,因此也具有两个比较明显的弱点:
(1)当数据量增大时,要求较大的内存支持I/O消耗也很大;
(2)当空间聚类的密度不均匀、聚类间距差相差很大时,聚类质量较差
DBSCAN密度聚类算法从样本的密度角度来考察样本之间的可连接性。简单来说,就是对一个样本点它,以它为中心,它周边一定区域内所含样本数达到阈值,则该样本点就属于一个领域内,且该样本所含区域范围内的样本点即为一个密度云,然后进行向外扩充。
基本定义:
- 领域:对于 xj 属于 数据集D,其领域包含样本集与xj的距离不大于 γ 的样本,即 N(xj) = { xj属于D | dist ( xi , xj ) <= γ }
- 核心对象: 若 xj 的领域中至少包含 MinPts 个样本,即 | N(xj)| >= MinPts ,则 xj 为一个核心对象
- 密度直达: 若xj位于xi的领域中,且xi也是一个核心对象,则称xj有xi密度直达
- 密度可达: 对xi与xj,若存在样本序列 p1,p2,..,pn,其中 p1 = xi , pn = xj ,且 pi+1 是由 pi 密度直达,则称xj由xi密度可达
- 密度相连:对xi与xj,若存在xk使得xi,xj均有xk密度可达,则xi,xj密度相连【我们做聚类主要就是找到一个样本点(简称密度云)的最大密度相连】
算法流程:
输入:样本集 D = { x1,x2,x3,...,xn }
领域参数 { γ , MinPts}
过程:
- 先找出整个样本中的核心对象集合 T
- 随机选取核心对象集合中的一个对象作为起始对象,寻找它的领域样本点集 L
- 对寻找出来的样本点集 L 做核心对象判断,符合核心对象的形成一个新的小核心对象点集 P,再对 P 重复第二步,直到循环结束输出一个全体的样本点集 E
- 原来的核心对象集合 T - E ,留下来的为剩下的核心对象集合, E 为分好的簇,重复第二步直到核心对象集合 T 中没有核心对象
高斯混合聚类(概率模型聚类)
简单来说这个聚类方式就是,我事先告诉算法有需要有几个分类,然后通过随机样本,然后以随机后的样本求其后验分布。求出其后验分布后(簇的划分即为后验概率最大的一方)。再通过求出的后验概率去对原先假设的样本进行更新迭代,使其趋向于最优解(这时候就是通过极大似然估计去逼近最优值,来更新样本)这里我们可以假设我们的分类概率是一个隐变量,那么这样子的求解方式就是EM算法:详见(另一篇文章)
其实EM算法与反向传播的概念基本上是相同,在反向传播中,我们先假设一个参数求出一个 y值解,将这个解值去与真实值比较,后会产生一个损失函数,目的是使损失函数不断的减小从而更新假设值。EM算法其实也是相同的,稍微不同的是,这里没有真实值去进行逼近,而是通过对每次的假设与极大似然估计进行逼近,在两者达到一定阈值或者到一定迭代次数时候即为最佳。
算法流程:
输入:样本集 D = { x1,x2,x3,...,xm }
高斯混合成分个数k
过程:
初始化高斯混合分布函数 a,u,Z
a = 1 / k
u = 随机的选择连续函数在高斯分布中的值
Z = (还有待研究)
- 先计算其所有的样本K的对于D中每个样本的后验概率
- 更新a,u,Z的值(通过极大似然估计),迭代循环到第一步
- 根据后验概率选择分类