最近重温了一下线段树,发现暑假学得太囫囵吞枣,某些细节没有真正理解,学算法还是要脚踏实地啊(日常鸡汤)!下面来总结一下线段树。
线段树是什么?有什么用?
线段树类似区间树,它在各个节点保存一条线段(数组中的一段子数组),主要用于高效解决连续区间的动态查询问题,由于二叉结构的特性,它基本能保持每个操作的复杂度为O(logn)。
你可能会问:查询区间和可以用O(n)的复杂度预处理一个前缀和数组,然后就可以O(1)地查询某段区间和;查询区间最值,也就是RMQ问题,也可以用O(nlogn)的复杂度预处理ST表,然后O(1)地查询区间最值。那么为什么要使用线段树呢?
线段树的精髓就在于它能在支持区间动态修改的前提下保持每个操作O(logn)的复杂度,这是其他两者做不到的。
线段树能进行的操作主要有:1)单点更新,区间查询 2)区间更新,区间查询 3)区间更新,单点查询
除了上述操作,线段树还可以解决区间染色和矩形面积交、面积并等问题。
线段树基本知识
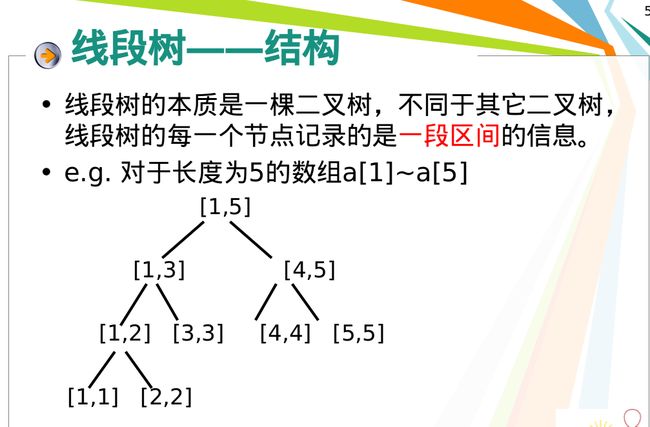
线段树的结构:
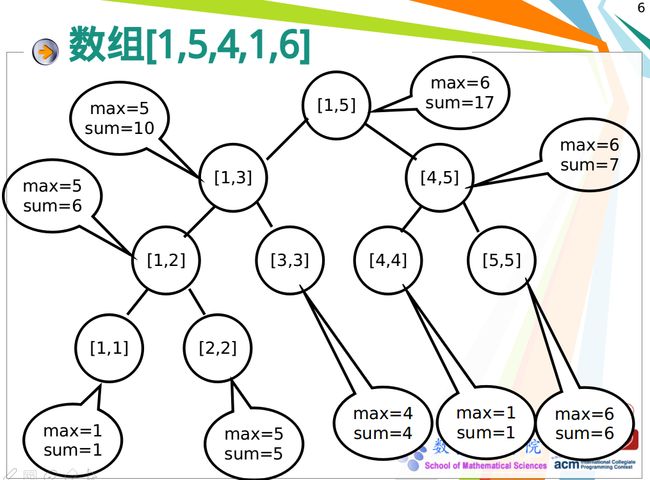
建立一个线段树的示意图(可以维护区间和或最值):
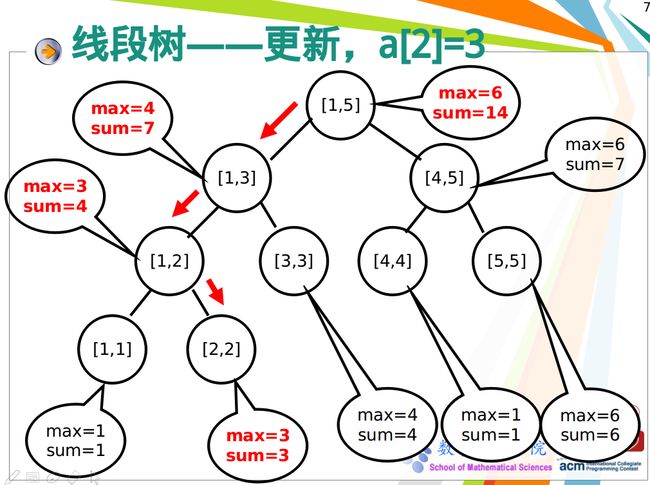
单点修改后重新调整线段树:
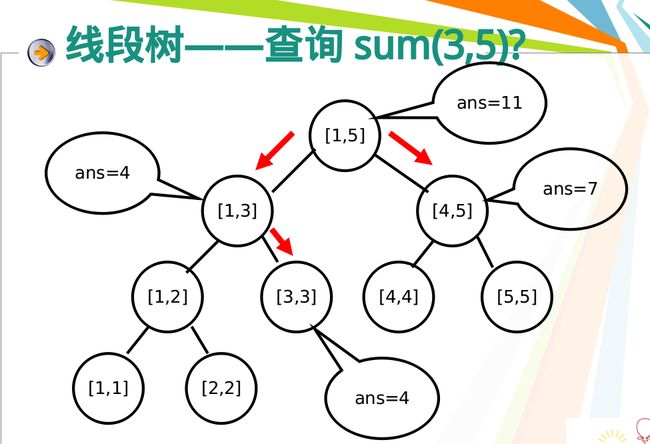
区间查询区间最值:
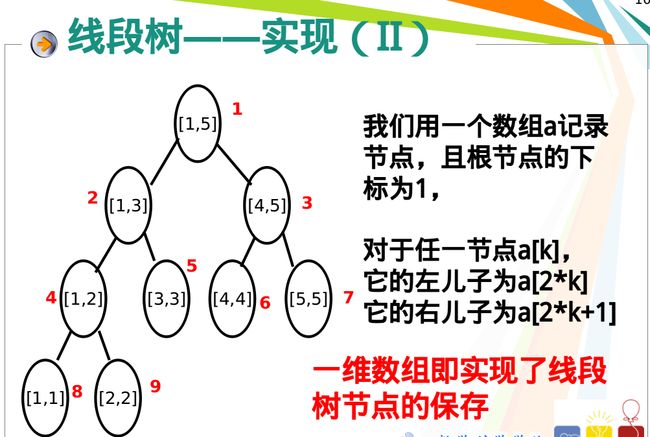
线段树的结点关系:
线段树的代码实现
下面给出建立线段树和进行各种操作的模板,关键点在代码的注释中有解释:
/*node:区间结点号 begin:该node的区间左边界 end:该node的区间右边界
left:查询区间的左边界 right:查询区间的右边界 pos:查询区间的点*/
/*线段树:求和或最值
单点更新,区间查询
区间更新,单点查询(lazy标记表示本节点的信息已经根据标记更新过了,但是本节点的子节点仍需要进行更新。lazy初始为0,区间加上k给该区间管理的结点的lazy加k,push_down给子节点加(end-begin+1)*k)
区间更新,区间查询
lson 2*node
rson 2*node+1
[begin,end]
[begin,mid] [mid+1,end] 其中mid为(begin+end)/2 */
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
int segTree[maxn*4];
int lazy[maxn*4];
void pushUp(int node){//pushUp自底向上更新区间和与最值
segTree[node]=segTree[lson]+segTree[rson];//segTree[node]=max(segTree[lson],segTree[rson])
}
void pushDown(int node,int begin,int end){//pushDown自顶向下更新lazy数组和给结点加上lazy数组的值
if(!lazy[node]) return;//lazy[node]为0直接return
segTree[lson]+=(mid-begin+1)*lazy[node];
segTree[rson]+=(end-mid)*lazy[node];
lazy[lson]+=lazy[node];
lazy[rson]+=lazy[node];//给左右孩子传递lazy,是+=不是=,因为孩子节点可能被多次延迟标记又没有向下传递
lazy[node]=0;//把父节点的lazy置为0
}
void build(int node,int begin,int end){//建树
lazy[node]=0;
if(begin==end){//begin==end表示管理的是结点
scanf("%d",&segTree[node]);//按照顺序输入结点,由于建树类似于树的先根遍历,所以建立的线段树的叶子结点从左到右的值就是输入的顺序
//segTree[node]=a[begin] 用于任意顺序输入,先将输入存入a数组,下标从1开始,begin = end = index
return;//输入完成后要return,否则会继续访问左右孩子,可能越界
}
build(lson,begin,mid);
build(rson,mid+1,end);
pushUp(node);
}
void update(int node,int begin,int end,int pos,int k){//单点更新
if(posend) return;//管理的区间不包含pos,直接return
if(begin==end){
segTree[node]+=k;
return;
}
update(lson,begin,mid,pos,k);
update(rson,mid+1,end,pos,k);
pushUp(node);
}
int query(int node,int begin,int end,int left,int right){//区间查询
if(left>end||right=end) return segTree[node];//查询区间包含查询结点
pushDown(node,begin,end);
int sum=0;//int maxx=-1
sum+=query(lson,begin,mid,left,right);//maxx=max(maxx,query(lson,begin,mid,left,right))
sum+=query(rson,mid+1,end,left,right);//maxx=max(maxx,query(rson,mid+1,end,left,right))
return sum;
}
void update(int node,int begin,int end,int left,int right,int k){//区间更新
if(left>end||right=end){//更新区间包含结点
segTree[node]+=(end-begin+1)*k;
lazy[node]+=k;
return;
}
pushDown(node,begin,end);
update(lson,begin,mid,left,right,k);
update(rson,mid+1,end,left,right,k);
pushUp(node);
}
例题
一、单点更新,区间查询
HDU1166 敌兵布阵
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1166
代码:
#include
#define maxn 50005
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
using namespace std;
int segTree[maxn*4];
int T,N,a,b;
char command[10];
void pushUp(int node){
segTree[node]=segTree[lson]+segTree[rson];
}
void build(int node,int begin,int end){
if(begin==end){
scanf("%d",&segTree[node]);
return;
}
build(lson,begin,mid);
build(rson,mid+1,end);
pushUp(node);
}
void update(int node,int begin,int end,int pos,int k){
if(posend) return;
if(begin==end){
segTree[node]+=k;
return;
}
update(lson,begin,mid,pos,k);
update(rson,mid+1,end,pos,k);
pushUp(node);
}
int query(int node,int begin,int end,int left,int right){
if(left>end||right=end) return segTree[node];
int sum=0;
sum+=query(lson,begin,mid,left,right);
sum+=query(rson,mid+1,end,left,right);
return sum;
}
int main(){
scanf("%d",&T);
int cas=1;
while(T--){
scanf("%d",&N);
build(1,1,N);
printf("Case %d:\n",cas++);
while(scanf("%s",command)!=EOF){
if(command[0]=='E') break;
scanf("%d%d",&a,&b);
if(command[0]=='Q')
cout< HDU 1754 I Hate It
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1754
代码:
#include
#define maxn 200005
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
using namespace std;
int segTree[4*maxn];
int N,M,A,B;
char C[3];
void pushUp(int node){
segTree[node]=max(segTree[lson],segTree[rson]);
}
void build(int node,int begin,int end){
if(begin==end){
scanf("%d",&segTree[node]);
return;
}
build(lson,begin,mid);
build(rson,mid+1,end);
pushUp(node);
}
void update(int node,int begin,int end,int pos,int k){
if(posend) return;
if(begin==end){
segTree[node]=k;//直接修改
return;
}
update(lson,begin,mid,pos,k);
update(rson,mid+1,end,pos,k);
pushUp(node);
}
int query(int node,int begin,int end,int left,int right){
if(left>end||right=end) return segTree[node];
int maxx=0;
maxx=max(maxx,query(lson,begin,mid,left,right));
maxx=max(maxx,query(rson,mid+1,end,left,right));
return maxx;
}
int main(){
while(scanf("%d%d",&N,&M)!=EOF){
build(1,1,N);
while(M--){
scanf("%s%d%d",C,&A,&B);
if(C[0]=='Q'){
printf("%d\n",query(1,1,N,A,B));
}
else{
update(1,1,N,A,B);
}
}
}
}
二、区间更新,区间查询
POJ 3468 A Simple Problem with Integers
题目链接:http://poj.org/problem?id=3468
代码:
#include
#define maxn 100005
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
using namespace std;
typedef long long ll;
ll segTree[4*maxn];
ll lazy[4*maxn];
ll N,Q,A,B,C;
char command[3];
void pushUp(ll node){
segTree[node]=segTree[lson]+segTree[rson];
}
void pushDown(ll node,ll begin,ll end){
if(!lazy[node]) return;
segTree[lson]+=(mid-begin+1)*lazy[node];
segTree[rson]+=(end-mid)*lazy[node];
lazy[lson]+=lazy[node];
lazy[rson]+=lazy[node];
lazy[node]=0;
}
void build(ll node,ll begin,ll end){
lazy[node]=0;
if(begin==end){
scanf("%lld",&segTree[node]);
return;
}
build(lson,begin,mid);
build(rson,mid+1,end);
pushUp(node);
}
ll query(ll node,ll begin,ll end,ll left,ll right){
if(left>end||right=end) return segTree[node];
pushDown(node,begin,end);
ll sum=0;
sum+=query(lson,begin,mid,left,right);
sum+=query(rson,mid+1,end,left,right);
return sum;
}
void update(ll node,ll begin,ll end,ll left,ll right,ll k){
if(left>end||right=end){
segTree[node]+=(end-begin+1)*k;
lazy[node]+=k;
return;
}
pushDown(node,begin,end);
update(lson,begin,mid,left,right,k);
update(rson,mid+1,end,left,right,k);
pushUp(node);
}
int main(){
scanf("%lld%lld",&N,&Q);
build(1,1,N);
while(Q--){
scanf("%s",command);
if(command[0]=='Q'){
scanf("%lld%lld",&A,&B);
printf("%lld\n",query(1,1,N,A,B));
}
else{
scanf("%lld%lld%lld",&A,&B,&C);
update(1,1,N,A,B,C);
}
}
}
HDU 1698 Just A Hook
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1698
代码:
#include
#define maxn 100005
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
using namespace std;
int segTree[4*maxn];
int lazy[4*maxn];
int T,N,Q,X,Y,Z;
void pushUp(int node){
segTree[node]=segTree[lson]+segTree[rson];
}
void build(int node,int begin,int end){
lazy[node]=0;
if(begin==end){
segTree[node]=1;
return;
}
build(lson,begin,mid);
build(rson,mid+1,end);
pushUp(node);
}
void pushDown(int node,int begin,int end){
if(!lazy[node]) return;
segTree[lson]=(mid-begin+1)*lazy[node];//+=改成=,直接更新到底部
segTree[rson]=(end-mid)*lazy[node];
lazy[lson]=lazy[node];
lazy[rson]=lazy[node];
lazy[node]=0;
}
void update(int node,int begin,int end,int left,int right,int k){
if(left>end||right=end){
segTree[node]=(end-begin+1)*k;//+=改成=,直接更新到底部
lazy[node]=k;//+=改成=,因为此时lazy即使没有下传也不叠加
return;
}
pushDown(node,begin,end);
update(lson,begin,mid,left,right,k);
update(rson,mid+1,end,left,right,k);
pushUp(node);
}
int query(int node,int begin,int end,int left,int right){
if(left>end||right=end) return segTree[node];
pushDown(node,begin,end);
int sum=0;
sum+=query(lson,begin,mid,left,right);
sum+=query(rson,mid+1,end,left,right);
return sum;
}
int main(){
scanf("%d",&T);
int cas=1;
while(T--){
scanf("%d%d",&N,&Q);
build(1,1,N);
while(Q--){
scanf("%d%d%d",&X,&Y,&Z);
update(1,1,N,X,Y,Z);
}
printf("Case %d: The total value of the hook is %d.\n",cas++,query(1,1,N,1,N));
}
}
三、区间染色问题
ZOJ 1610 Count the Colors
题目链接:https://vjudge.net/problem/11553/origin
代码:
#include
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
#define maxn 8005
using namespace std;
int col[maxn*4];//col[node]表示node管辖的区间的颜色
int sum[maxn];//表示某点的颜色
int res[maxn];
void pushDown(int node){
col[lson]=col[rson]=col[node];
col[node]=-1;
}
void update(int node,int begin,int end,int left,int right,int k){
if(left>end||right=end){
col[node]=k;
return;
}
if(col[node]!=-1) pushDown(node);
update(lson,begin,mid,left,right,k);
update(rson,mid+1,end,left,right,k);
}
//不用建树,直接在query里存储颜色即可,因为染色不用求区间和或者最值
void query(int node,int begin,int end,int left,int right){
if(begin==end){
sum[begin]=col[node];//存储每个点的颜色
return;
}
if (col[node] != -1) pushDown(node);
query(lson,begin,mid,left,right);
query(rson,mid+1,end,left,right);
}
int main(){
int n,x1,x2,c;
while(scanf("%d",&n)!=EOF){
memset(col,-1,sizeof(col));
memset(sum,-1,sizeof(sum));
memset(res,0,sizeof(res));
for(int i=0;i=L
update(1,0,maxn-1,x1,x2-1,c);//为防止重叠,更新区间[L,R-1]
/*注意begin=0 end=maxn-1 而不是begin=1 end=n 因为只是涂n次,不一定在1-n范围内涂 */
}
query(1,0,maxn-1,0,maxn-1);
for(int i=0; i POJ 2528 Mayor's posters
题目链接:http://poj.org/problem?id=2528
代码:
/*解法:离散化,如下面的例子(题目的样例),因为单位1是一个单位长度,将下面的
1 2 3 4 6 7 8 10
— — — — — — — —
1 2 3 4 5 6 7 8
离散化 X[1] = 1; X[2] = 2; X[3] = 3; X[4] = 4; X[5] = 6; X[7] = 8; X[8] = 10
于是将一个很大的区间映射到一个较小的区间之中了,然后再对每一张海报依次更新在宽度为1~8的墙上(用线段树),最后统计不同颜色的段数。
但是只是这样简单的离散化是错误的,
如三张海报为:1~10 1~4 6~10
离散化时 X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 6, X[ 4 ] = 10
第一张海报时:墙的1~4被染为1;
第二张海报时:墙的1~2被染为2,3~4仍为1;
第三张海报时:墙的3~4被染为3,1~2仍为2。
最终,第一张海报就显示被完全覆盖了,于是输出2,但实际上明显不是这样,正确输出为3。
新的离散方法为:在相差大于1的数间加一个数,例如在上面1 4 6 10中间加5(算法中实际上1,4之间,6,10之间都新增了数的)
X[ 1 ] = 1, X[ 2 ] = 4, X[ 3 ] = 5, X[ 4 ] = 6, X[ 5 ] = 10
这样之后,第一次是1~5被染成1;第二次1~2被染成2;第三次4~5被染成3
最终,1~2为2,3为1,4~5为3,于是输出正确结果3。*/
#include
#include
#include
#define lson (node<<1)
#define rson ((node<<1)|1)
#define mid ((begin+end)>>1)
using namespace std;
#define maxn 10005
//不用建树,直接在query里记录hash即可,因为染色不用求区间和或者最值,也不用pushUp
int m, li[maxn], ri[maxn];
int poster[maxn<<3], col[maxn<<4], ans; //col记录当前该位置最上面一层的海报种类,即染色问题的颜色
//poster记录海报位置
bool hash[maxn];//hash用于标记某种种类的海报是否计算过,若已计算过标记为true,不再重复计算
void pushDown(int node) {
col[lson] = col[rson] = col[node];//类似lazy标记,向下传递后清空
col[node] = -1;
}
void update(int node,int begin, int end,int left, int right, int k) {
if(left>end||right= left && end <= right) {
col[node] = k;
return;
}
if(col[node] != -1) pushDown(node);
update(lson,begin,mid,left,right,k);
update(rson,mid+1,end,left,right,k);
}
void query(int node,int begin,int end) {
if (begin == end) {
if (!hash[col[node]]) {
ans++;
hash[col[node]] = true;
}
return;
}
if (col[node] != -1) pushDown(node);
query(lson,begin,mid);
query(rson,mid+1,end);
}
int binarySearch(int ll, int hh, int xx) {
int mm;
while (ll <= hh) {
mm = (ll + hh) >> 1;
if (poster[mm] == xx) return mm;
else if (poster[mm] > xx) hh = mm - 1;
else ll = mm + 1;
}
return -1;
}
int main()
{
int t, n, i;
scanf ("%d", &t);
while (t--) {
memset(col, -1, sizeof (col));//-1表示没有染色
memset (hash, false, sizeof (hash));/*因为本题墙的长度为10000000,
直接做会超时,而实际海报数量只有10000,考虑把每张海报左右两端的两段映射到小范围计算,
所以考虑离散化,但传统离散化会出错,要如果有两个位置相邻的数字数值不相邻,考虑在中间
插入一个比大的数小1的数*/
int cnt = 0;
scanf ("%d", &n);
for (i = 1; i <= n; i++) {
scanf ("%d %d", &li[i], &ri[i]);
poster[++cnt] = li[i];
poster[++cnt] = ri[i];
}
sort(poster+1, poster+cnt+1);
m = 1;
for (i = 2; i <= cnt; i++) {
if (poster[i] != poster[i-1]) poster[++m] = poster[i];//去重
}
for (i = m; i > 1; i--) {
if (poster[i] - poster[i-1] > 1) poster[++m] = poster[i] - 1;//在末尾加入要增加的点
}
sort(poster+1, poster+m+1);//重新排序
for (i = 1; i <= n; i++) {
int l = binarySearch(1, m, li[i]);//在离散化后的poster数组里二分查找每一组的左右端点
int r = binarySearch(1, m, ri[i]);
update(1,1,m,l,r,i);
}
ans = 0;
query(1, 1, m);
printf("%d\n", ans);
}
return 0;
}
四、矩形面积交/面积并
HDU 1542 Atlantis(矩形面积并)
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1542
代码:
#include
#define lson (rt<<1)
#define rson ((rt<<1)|1)
#define mid ((l+r)>>1)
#define maxn 2005
using namespace std;
int n;
double y[maxn];
//沿x轴扫描,沿y轴建树,线段树的结点是纵向的线段,最下面一层结点以排序后相邻的y1,y2为边界
struct LINE // 存储线段信息;
{
double x; // 该线段的x坐标;
double y_up,y_down; // 竖向线段的上下端点;
int flag;//矩形的左边界为1,右边界为-1
}line[maxn];
struct node//线段树的结点,不再是单个点,是一个区间
{
double l,r; // 区间的左右边界,即某段扫描线的上下端点
double x; // 记录上一个横坐标位置,用于求面积;
int cover; // 记录覆盖的线段数;即同一方向的线段数;由flag累加
bool flag; // 标记只有一个区间的节点,即在线段树最底层的结点,我们将一个个连续的区间离散化成一个结点;
}node[maxn<<2];
bool cmp(LINE a,LINE b)
{
return a.x=node[rt].r||r<=node[rt].l) return 0; // 该方向结点不包含所要查询的区间;
if(node[rt].flag){ // 找到只有一个区间的叶子结点;
if(node[rt].cover>0){
double pre=node[rt].x;
double ans=(x-pre)*(node[rt].r-node[rt].l); // 计算面积;
node[rt].x=x; // 更新定位x位置,便于下次计算面积;
node[rt].cover+=flag; // 更新覆盖的线段数;
return ans;
}
else{
node[rt].x=x;
node[rt].cover+=flag;
return 0;//没有产生面积并也要return 0
}
}
double ans1,ans2;
ans1=Insert_query(lson,x,l,r,flag);
ans2=Insert_query(rson,x,l,r,flag);
return ans1+ans2;
}
int main()
{
int Case=0;
double x1,x2,y1,y2;
while(~scanf("%d",&n)&&n){
int cnt=0;
for(int i=0;i HDU 1255 覆盖的面积(矩形面积交)
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=1255
代码:
#include
#define lson (rt<<1)
#define rson ((rt<<1)|1)
#define mid ((l+r)>>1)
#define maxn 2005
using namespace std;
int T,N;
double y[maxn];
struct LINE{
double x;
double y_up,y_down;
int flag;
}line[maxn];
struct node{
double l,r;
double x;
int cover;
bool flag;
}node[maxn<<2];
bool cmp(LINE a,LINE b){
return a.x=node[rt].r||r<=node[rt].l) return 0;
if(node[rt].flag){
if(node[rt].cover>1){
double pre=node[rt].x;
double ans=(x-pre)*(node[rt].r-node[rt].l);
node[rt].x=x;
node[rt].cover+=flag;
return ans;
}
else{
node[rt].x=x;
node[rt].cover+=flag;
return 0;
}
}
double ans1,ans2;
ans1=Insert_query(lson,x,l,r,flag);
ans2=Insert_query(rson,x,l,r,flag);
return ans1+ans2;
}
int main(){
scanf("%d",&T);
while(T--){
int cnt=0;
scanf("%d",&N);
while(N--){
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
y[cnt]=y1;
line[cnt].x=x1;
line[cnt].y_down=y1;
line[cnt].y_up=y2;
line[cnt++].flag=1;
y[cnt]=y2;
line[cnt].x=x2;
line[cnt].y_down=y1;
line[cnt].y_up=y2;
line[cnt++].flag=-1;
}
sort(y,y+cnt);
sort(line,line+cnt,cmp);
build(1,0,cnt-1);
double area=0;
for(int i=0;i