折半查找法又称为二分查找法。
(一)基本思想
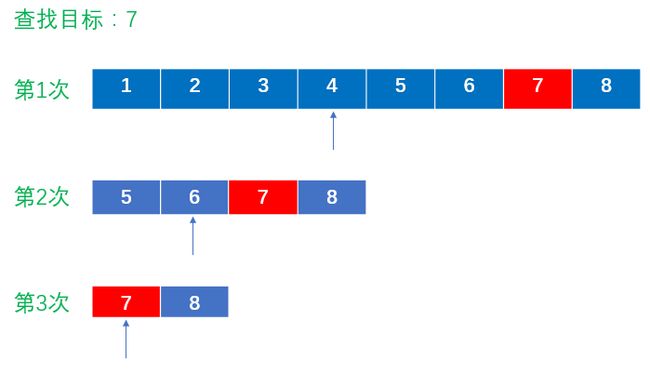
假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。
重复以上过程,直到找到满足条件的记录,此时查找成功;或直到子表不存在为止,此时查找不成功。
(二)时间复杂度
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x
时间复杂度就是求while循环的次数。
假设总共有n个元素,每次查找的区间大小就是n,n/2,n/4,…,n/2^k,其中k就是循环的次数。
由于n/2^k取整后>=1,令n/2^k=1, 可得k=log2(n),(以2为底n的对数)。
所以时间复杂度可以表示为O(h)=O(log2(n))
(三)优缺点
优点是比较次数少,查找速度快,平均性能好;
缺点是要求待查表为有序表,且插入删除困难。
因此,折半查找方法适用于不经常变动而查找频繁的有序列表。
(四)代码实现
1 C语言,递归实现
#include
int recur_bin_search(int a[], int low, int high, int key)
{
if(low > high)
{
return -1;
}
int mid = (low + high) / 2;
if(key == a[mid])
{
return mid;
}
else if(key < a[mid])
{
return recur_bin_search(a, low, mid - 1, key);
}
else
{
return recur_bin_search(a, mid + 1, high, key);
}
}
int main()
{
int a[] = {1, 2, 3, 4, 5, 6, 7, 8};
int num = 7;
int size = sizeof(a) / sizeof(int);
int index = recur_bin_search(a, 0, size - 1, num);
if(-1 == index)
{
printf("Not found\n");
}
else
{
printf("Index of %d is %d\n", num, index);
}
return 0;
}
运行结果:
Index of 7 is 6
2 C++,非递归实现实现
#include
using namespace std;
#ifndef SEARCH_METHODS
#define SEARCH_METHODS
template
int BinSearch(T array[], int n, T key)
{
int mid, low ,high;
T midvalue;
low = 0;
high = n - 1;
while(low <= high)
{
mid = (low + high) / 2;
midvalue = array[mid];
if(key == midvalue)
{
return mid;
}
else if(key < midvalue)
{
high = mid-1;
}
else
{
low = mid+1;
}
}
return -1;
}
#endif
int main()
{
int a[] = {1, 2, 3, 4, 5, 6, 7, 8};
int num = 7;
int size = sizeof(a) / sizeof(int);
int index = BinSearch(a, size, num);
if(-1 == index)
{
cout << "Not found" << endl;
}
else
{
cout << "Index of " << num << " is " << index << endl;
}
return 0;
}
3 Java,非递归实现
package com.z;
public class Search {
public static int binarySearch(int a[], int goal) {
int low = 0;
int high = a.length-1;
while (low <= high) {
int middle = (low + high)/2;
if (goal == a[middle]) {
return middle;
} else if (a[middle] > goal) {
high = middle - 1;
} else {
low = middle + 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] src = new int[] {1, 2, 3, 4, 5, 6, 7, 8};
int index = binarySearch(src, 7);
if( -1 == index) {
System.out.println("The goal not found.");
} else {
System.out.println("The index of the goal is: " + index);
}
}
}
运行结果:
The index of the goal is: 6
4 Python,递归和非递归实现
#coding:utf-8
a = [1, 2, 3, 4, 5, 6, 8, 10, 20, 30, 40]
b = 9
c = 5
#-----------------递归二分查找-------------------------
def recur_bin_search(array, left, right, key):
mid = left + (right - left) / 2
if(left > right):
print 'The number not found'
return -1
else:
if(array[mid] > key):
return recur_bin_search(array, left, mid - 1, key)
elif(array[mid] < key):
return recur_bin_search(array, mid + 1, right, key)
else:
print 'The number has found, the index is: '
return mid
print recur_bin_search(a, 0, len(a) - 1, b)
#-------------------非递归二分查找---------------------
def bin_search(array, key):
low = 0
high = len(array) - 1
while low <= high:
mid = (low + high) / 2
if key == a[mid]:
print 'The number has found, the index is: '
return mid
elif a[mid] < key:
low = mid + 1
else:
high = mid - 1
print 'The number not found'
return -1
print bin_search(a, c)
#-------------------------------------------------------
input('Press any key to exit')
运行结果:
The number not found
-1
The number has found, the index is:
4
更多内容请关注微信公众号