一、语言模型
语言模型计算特定序列中多个单词的出现概率。一个 m 个单词的序列 的概率定义为 。
传统的语言模型为了简化问题,引入了马尔科夫假设,即句子的概率通常是通过待预测单词之前长度为n的窗口建立条件概率来预测:
简单来说就是每次考虑都当前词前面所有的词的信息显然对是很冗余的,因为离当前词越远的词通常和当前词没多少联系了,那么就干脆我们就取离当前词最近的几个词的信息来替代当前词前面所有词的信息。嗯,人之常情,很好理解。
例如,考虑一种情况,有一篇文章是讨论西班牙和法国的历史,然后在文章的某个地方,你读到一句话 “The two country went on a battle”;显然,这句话中提供的信息不足以确定文章所讨论的两个国家的名称(法国和西班牙)。
二、循环神经网络
传统的翻译模型只能以有限窗口大小的前 n 个单词作为条件进行语言模型建模,循环神经网络与其不同,RNN 有能力以语料库中所有前面的单词为条件进行语言模型建模。
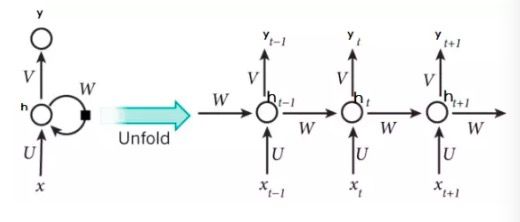
下图展示的 RNN 的架构,其中矩形框是在一个时间步的一个隐藏层 :
如上图所示:
RNNs包含输入单元(Input units),输入集标记为{},是含有 T 个单词的语料库对应的词向量
输出单元(Output units)的输出集标记为{},是在每个时间步 t 全部单词的概率分布输出,用公式表示为
RNNs还包含隐藏单元(Hidden units),{},表示每个时间步 t 的隐藏层的输出特征的计算关系,可以理解成RNN的记忆
准确来讲,RNN其实就是一个网络的多次复用:
其中:
如果将每一个复用都展开的话:
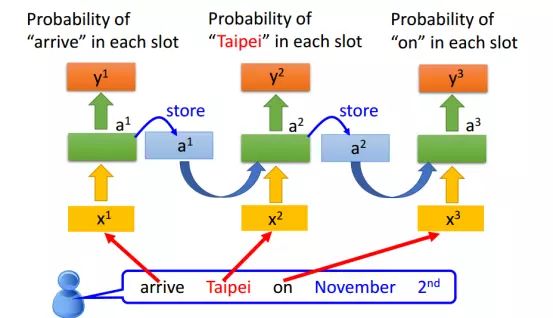
RNN的一个实际小例子:
三、BPTT
其实从理解上RNN其实很好理解,毕竟很直观,因为想囊获前面所有的信息,所以每次都计算一个(这里使用网络得到,但是其实最简单的囊获前面所有信息的方式就是累加,只是效果不好而已)。
但RNN麻烦的地方就在于它的求导,由于循环操作,这就导致更新权值的时候会牵一发而动全身。
如下图的RNN:
首先写出前向公式:
损失函数:
其中:T是序列长度,在这里就是3(为了好理解,此次的推导会先按T=3进行,然后再推广到一般)
3.1 对 的求导
对于 的求导显然不难,但是要注意的是,由于RNN是循环的网络,所有导致每一个时刻的都对 有关,所以求导会变成加和的形式:
矩阵求导的具体矩阵应该怎么乘可以根据左右两边的维度来确定,如在上式中,由于 肯定是(output_num, hidden_num)维度,是标量对向量的求导,不难得到其维度为(output_num, 1),那么剩下的就只能是转置的形式。当然,由于这里不涉及行向量对行向量求导或者列向量对列向量求导,所以可以用简单的矩阵求导法则得到一样的结果,但如果出现行向量对行向量求导或者列向量对列向量求导的情况,还是只能使用这样的维度匹配。
3.2 对 的求导
对于 的求导就会变得更复杂一点,因为不仅是,隐藏层之间也存在联系。
先考虑最简单的情况,当我们对求导时,由于没有其他和的牵制,所以可以很简单地写出其表达式:
那么我们将情况拓展到 ,由于也与其有关,所以最后可以写出表达式:
如果我们将对求导时的情况带入的话:
以此类推,我们就可以得到当t < 3时(或者说T时)的通用表达式:
那么将其他的带入通用形式变为:
可以看到这里有一个阶乘的项,这也就是导致RNN更容易产生梯度爆炸和消失的原因。
求出 的通用形式之后,对 的求导就变得简单了:
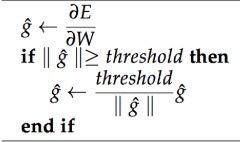
- 防止梯度爆炸:
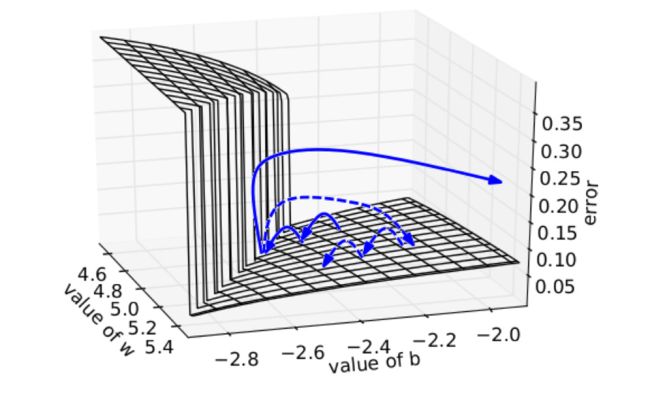
一种暴力的方法是,当梯度的长度大于某个阈值的时候,将其缩放到某个阈值。虽然在数学上非常丑陋,但实践效果挺好。其直观解释是,在一个只有一个隐藏节点的网络中,损失函数和权值w偏置b构成error surface,其中有一堵墙如下图所示,每次迭代梯度本来是正常的,一次一小步,但遇到这堵墙之后突然梯度爆炸到非常大,可能指向一个莫名其妙的地方(实线长箭头)。但缩放之后,能够把这种误导控制在可接受的范围内(虚线短箭头)。但这种trick无法推广到梯度消失,因为你不想设置一个最低值硬性规定之前的单词都相同重要地影响当前单词。
- 减缓梯度消失
- 不去随机初始化 ,而是初始化为单位矩阵
- 使用 Rectified Linear(ReLU)单元代替 sigmoid 函数,ReLU 的导数是 0 或者 1。这样梯度传回神经元的导数是 1,而不会在反向传播了一定的时间步后梯度变小
3.3 对 的求导
同理,我们可以轻松地写出:
到这里,我们基本上完成了RNN的求导,通过如下公式,便可以对RNN进行训练:
四、双向RNN
这部分就不展开了,主要因为理解上其实不难,就是在原来从左到右进行训练的基础上,又加了一个从右到左的顺序,整体原理和推导变化不大:
通过总结过去和未来词表示来预测下一个词的类别关系:
虽然看起来复杂,不过因为大部分库都已经封装了双向的操作,所以日常使用还是很轻松的,而且推导上其实也和原来的一样,只是要求的东西变多了而已。
五、LSTM
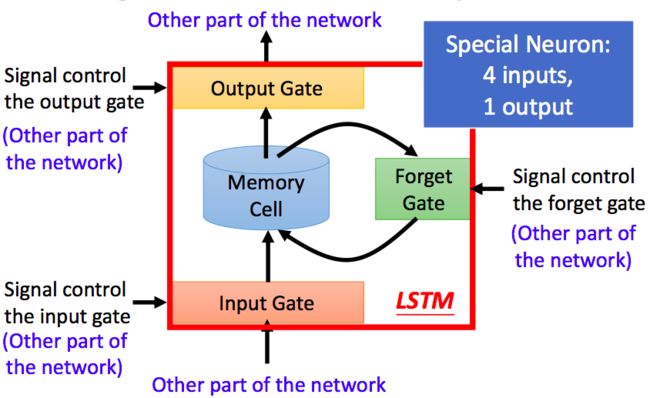
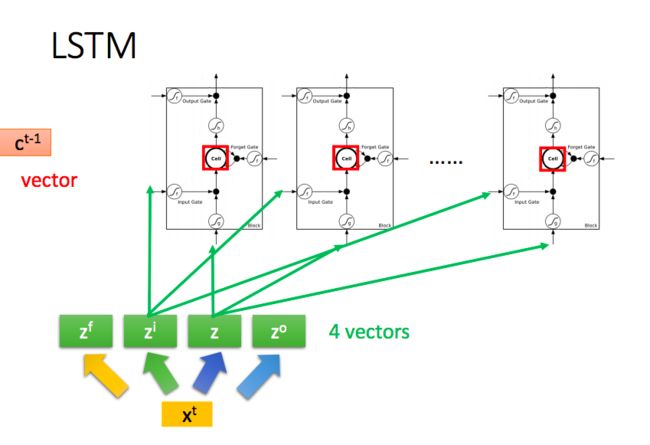
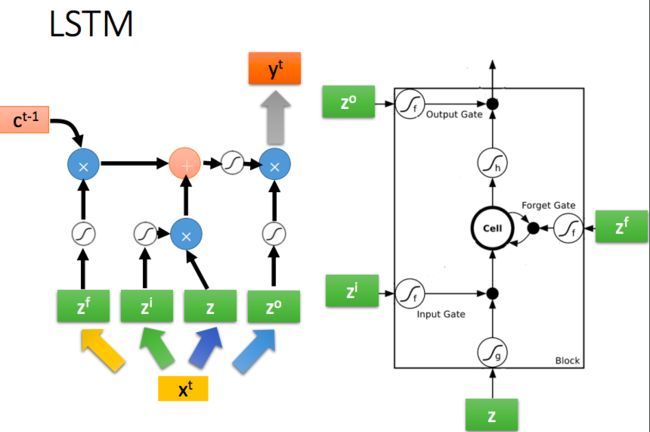
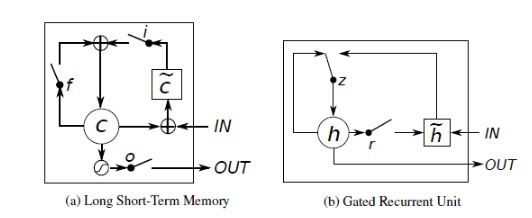
LSTM的全称是Long-Short-Term-Memories,其在原先RNN的基础上引入了门机制:
可以看到一共有4个门:
Input Gate:我们看到在生成新的记忆之前,新的记忆的生成阶段不会检查新单词是否重要,这需要输入门函数来做这个判断。输入门使用输入单词和过去的隐藏状态来决定输入值是否值得保留,从而决定该输入值是否加入到新的记忆中
Forget Gate:这个门与输入门类似,但是它不能决定输入单词是否有用,而是评估过去的记忆单元是否对当前记忆单元的计算有用,因此,忘记门观测输入单词和过去的隐藏状态并生成用来决定是否使用
New memory generation:生成新的记忆的阶段。我们基本上是用输入单词 和过去的隐藏状态来生成一个包括新单词 的新的记忆 (这个算不算门也因人而异,我个人是将其计算成门,所以一共是4个门)
Output/Exposure Gate:用处是将最终记忆与隐状态分离开来。记忆 中的信息不是全部都需要存放到隐状态中,隐状态是个很重要的使用很频繁的东西,因此,该门是要评估关于记忆单元 的哪些部分需要显露在隐藏状态 中。用于评估的信号是 ,然后与 通过 运算得到最终的 (注意,这里的和RNN里面其实不太一样,在LSTM里面,其实才是真正的)
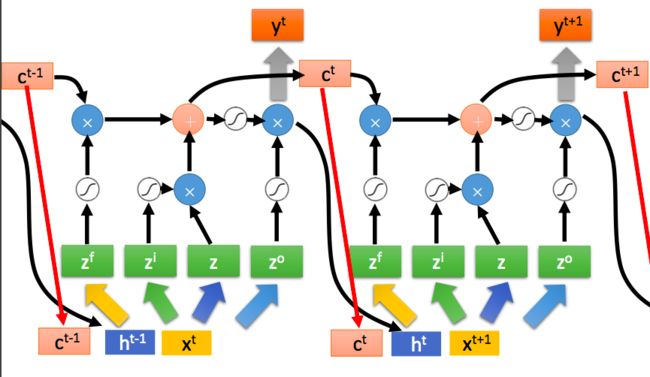
其他步骤:
- Final memory generation:这个阶段首先根据忘记门 的判断,相应地忘记过去的记忆 。类似地,根据输入门 的判断,相应地生成新的记忆 。然后将上面的两个结果相加生成最终的记忆 。
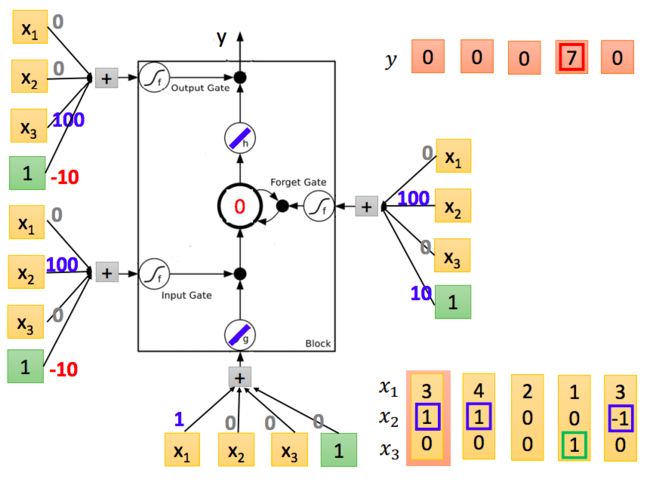
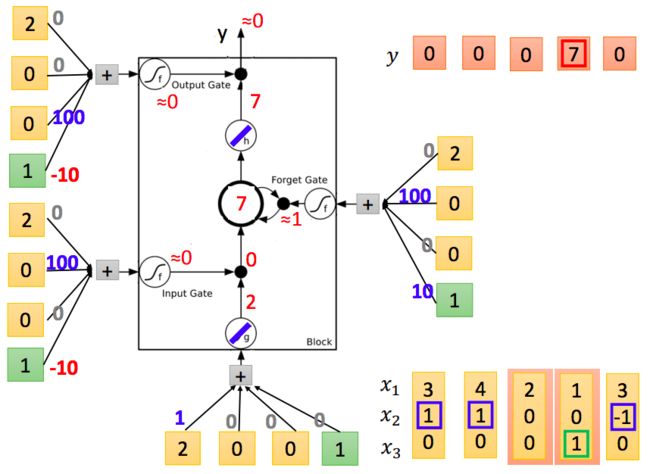
例子:
如上图所示,权值随机初始化,输入在右下角,接下来按顺序先输入[3,1,0]:
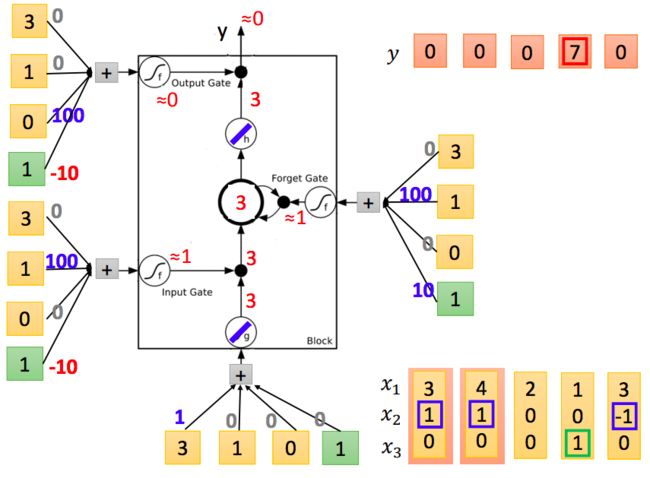
再输入[4,1,0]:
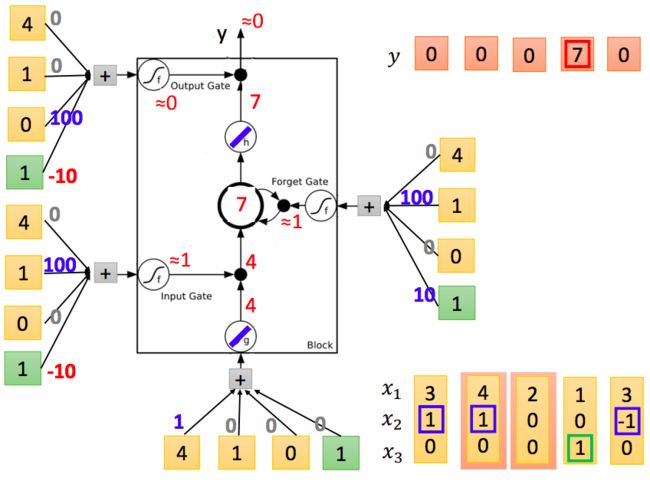
接下去以此类推:
整体上来看:
LSTM 如此复杂,那么它到底解决了什么问题呢?
观察LSTM的前向公式我们可以看到其实就是我们之前的 。那么如果对求导也会得到类似的阶乘的情况,但是此时被换成了(当然和之前求RNN的梯度一样,这里同样省略了其他东西,但大体上不影响结论),作为门机制的,它的取值基本上不是0就是1,但大多时候是1,(注意,遗忘门并是不为了解决梯度消失而出现,在最早的LSTM中是不存在遗忘门,而是直接把这里设置为1,这很有残差网络的味道)所以通过这样的结果很好地解决了传统RNN中梯度消失的问题。
当然这里仅仅解决了处的梯度问题,实际上LSTM在其他的梯度求导上还是容易出问题,这部分还是有待研究。至于遗忘门,查到的资料是说Gers 等人(2000)首先发现如果没有使记忆单元遗忘信息的机制,那么它们可能会无限增长,最终导致网络崩溃。为解决这个问题,他们为这个 LSTM 架构加上了另一个乘法门,即遗忘门。
六、GRU
GRU全称为Gated Recurrent Unit,它是LSTM的简化版变种,就目前的实验来看,GRU在性能上几乎与LSTM持平,但是在资源消耗方面会小一些。
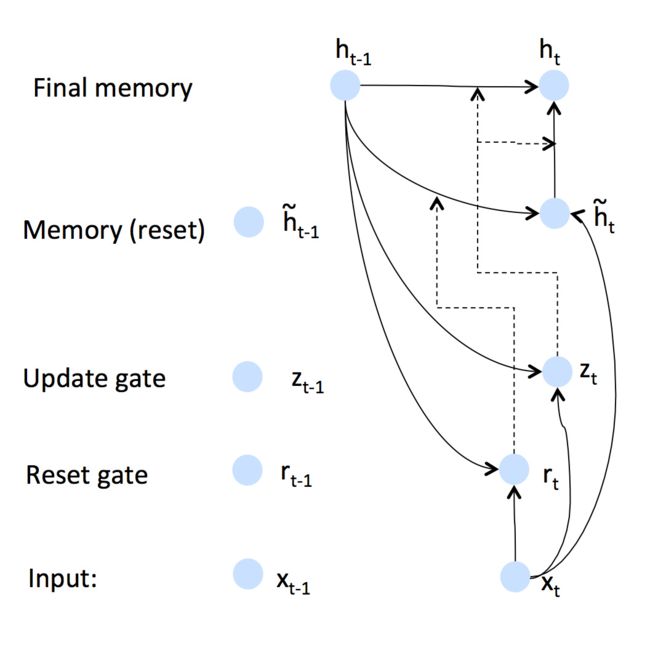
GRU对LSTM的门进行了删减整合,将遗忘门、输入门和输出门换成了更新门和重置门,即下图中的z和r:
更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门用于控制忽略前一时刻的状态信息的程度,重置门的值越小说明忽略得越多。
参考
- LSTM如何来避免梯度弥散和梯度爆炸?
- 三次简化一张图:一招理解LSTM/GRU门控机制
- LSTM如何解决梯度消失问题
- 详解 LSTM
- 学界|神奇!只有遗忘门的LSTM性能优于标准LSTM
- LSTM详解 反向传播公式推导
- CS224n笔记9 机器翻译和高级LSTM及GRU
- CS224n自然语言处理与深度学习 Lecture Notes Five
- Understanding LSTM Networks
- YJango的循环神经网络——实现LSTM
- GRU神经网络
- mxnet深度学习
- GRU与LSTM总结
- 李宏毅机器学习