2. 数据结构 - 树

这篇文章收录在我的 Github 上 algorithms-tutorial，另外记录了些算法题解，感兴趣的可以看看，转载请注明出处。

(一) 基本概念

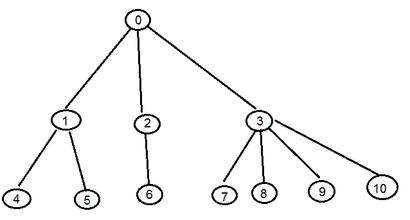
树是一种数据结构，它看上去像一棵 "圣诞树"，它的根在上，叶朝下。

树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

例如：

tree.jpg

树要吗为空树(empty tree)，要吗具有以下特性：

1. 每个节点可以有多个子节点(children)，而该节点是相应子节点的父节点(parent) - 比如说，1,2 是 0 的子节点，3 是 7,8 的父节点
2. 树有一个没有父节点的节点，称为根节点(root) - 比如图中的 0 节点
3. 没有子节点的节点称为叶节点(leaf) - 比如图中的 7，8，9，10 节点
4. 两个具有相同父节点的节点称为兄弟节点(sibling) - 比如图中 4，5 节点互为兄弟节点
5. 一个节点的子节点以及子节点的后代称为该节点的子树 (subtree) - 比如 1 和 1 的子节点构成了节点 0 的一棵子树

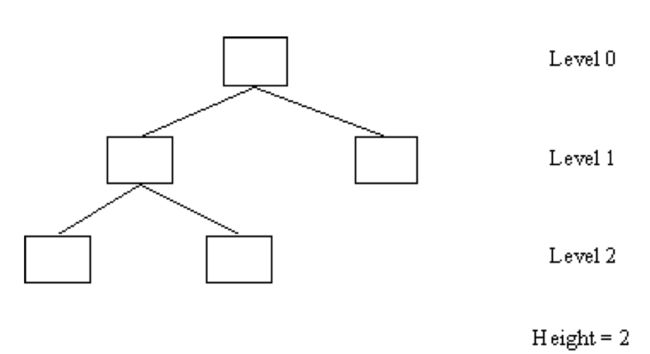
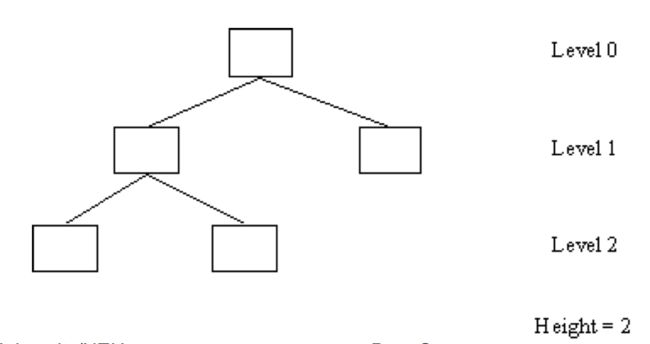
树的深度和高度的定义：(这里不太确定)

• 树的深度(depth)是从根节点开始（其深度为1）自顶向下逐层累加的
• 高度(height)也是从根节点开始（其高度为0）自顶向下逐层累加的

例如：该树深度为 3，高度为 2。

tree-level.png

我们将根节点定义为 level0，然后子节点逐层加一，直到叶节点。此时叶节点的 level 数即为树的高度。

(二) 二叉树 (Binary Tree)

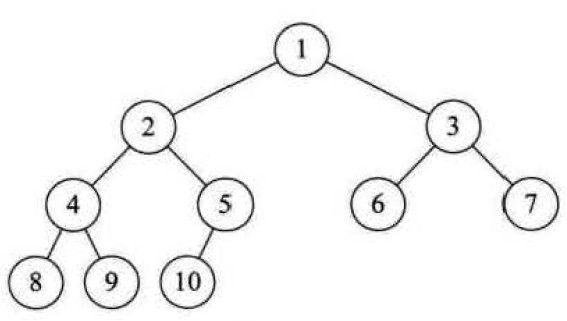
首先，二叉树(binary)是一种特殊的树，它是每个节点最多有两个子树的树结构，通常子树被称作是 "左子树" 和 "右子树"，二叉树常用于实现二叉搜索树和二叉堆。(这些在后面都会介绍)

例如: 下面这个就是一棵二叉树

binary-tree.jpg

常见的二叉树有：完全二叉树，满二叉树，二叉搜索树，二叉堆，AVL 树，红黑树，哈夫曼树。这些都会在后面一一介绍。

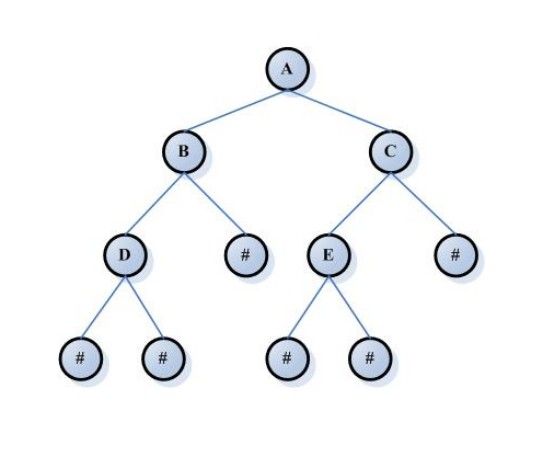
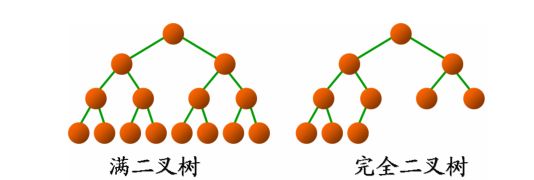
(三) 完全二叉树 (Complete Binary Tree)

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

例如:

complete-binary-tree.jpeg

即除了最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。而像这样就不是完全二叉树, 例如下图：(# 代表有元素)

binary-tree.jpg

用途：

完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高。后面介绍的二叉堆也是基于完全二叉树来实现的。

(五) 满二叉树 (Full Binary Tree)

很好理解，除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树被称之为满二叉树。

满二叉树一定是完全二叉树，完全二叉树不一定满二叉树。

例如：

compare.png

一个高度为 h 的满二叉树含有 1 + 2 + 4 + ... + 2^h = 2^(h + 1) - 1个节点，所以满二叉树的节点个数一定为奇数。

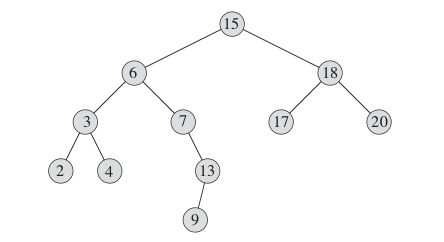
(六) 二叉搜索树 (Binary Search Tree)

二叉搜索树是一种特殊的二叉树，也可以称为二叉排序树，二叉查找树。除了具有二叉树的基本性质外，它还具备：

1. 树中每个节点最多有两个子树，通常称为左子树和右子树
2. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
3. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
4. 它的左右子树仍然是一棵二叉搜索树 (recursive)

例图：

binary-search-tree.png

基本操作：

在实行基本操作之前，我们需要先定义一下基本数据类型：

class TreeNode>{
    private E data;
    private TreeNode left;
    private TreeNode right;
    TreeNode(E theData){
        data = theData;
        left = null;
        right = null;
    }
}
public class BinarySearchTree>{
    private TreeNode root = null;
}

1.树的遍历：

假设我们需要遍历树中所有节点，这里有许多递归方法可以实现：

1.中序遍历：当到达某个节点时，先访问左子节点，再输出该节点，最后访问右子节点。

代码实现:

public void inOrder(TreeNode cursor){
    if(cursor == null) return;
    inOrder(cursor.getLeft());
    System.out.println(cursor.getData());
    inOrder(cursor.getRight());
}

2. 前序遍历：当到达某个节点时，先输出该节点，再访问左子节点，最后访问右子节点。

代码实现：

public void preOrder(TreeNode cursor){
    if(cursor == null) return;
    System.out.println(cursor.getData());
    inOrder(cursor.getLeft());
    inOrder(cursor.getRight());
}

3. 后序遍历：当到达某个节点时，先访问左子节点，再访问右子节点，最后输出该节点。

代码实现：

public void postOrder(TreeNode cursor){
    if(cursor == null) return;
    inOrder(cursor.getLeft());
    inOrder(cursor.getRight());
    System.out.println(cursor.getData());
}

2.树的搜索：

树的搜索和树的遍历差不多，就是在遍历的时候只搜索不输出就可以了。

例如：我们在树中搜索元素 20

search-element.gif

代码实现：

public boolean searchNode(TreeNode node){
    TreeNode currentNode = root;
    while(true){
        if(currentNode == null){
            return false;
        }
        if(currentNode.getData().compareTo(node.getData()) == 0){
            return true;
        }else if(currentNode.getData().compareTo(node.getData()) < 0){
            currentNode = currentNode.getLeft();
        }else{
            currentNode = currentNode.getRight();
        }
    }
}

3.节点插入：

步骤：

1. 递归地去查找该二叉树，找到应该插入的节点
2. 若当前的二叉查找树为空，则插入的元素为根节点
3. 若插入的元素值小于根节点值，则将元素插入到左子树中
4. 若插入的元素值不小于根节点值，则将元素插入到右子树中

比如：我们往树种插入元素 21

tree-insert-element.gif

代码实现：

public void insertNode(TreeNode node){
    TreeNode currentNode = root;
    if(currentNode == null){
        root = node;
        return;
    }else{
        while(true){
            if(node.getData().compareTo(currentNode.getData()) < 0){
                if(currentNode.getLeft() == null){
                    break;
                }else{
                    currentNode = currentNode.getLeft();
                }
            }else if(node.getData().compareTo(currentNode.getData()) > 0){
            
                if(currentNode.getRight() == null){
                    break;
                }else{
                    currentNode = currentNode.getRight();
                }
            }
        }   
    }
    if(node.getData().compareTo(currentNode.getData()) < 0){
        currentNode.setLeft(node);
    }else if(node.getData().compareTo(currentNode.getData()) > 0){
        currentNode.setRight(node);
    }
}

4.节点删除：

首先需要搜索该节点，然后可以分为以下四种情况进行讨论：

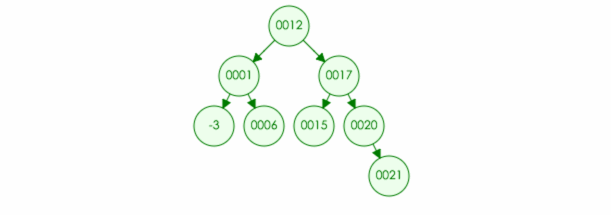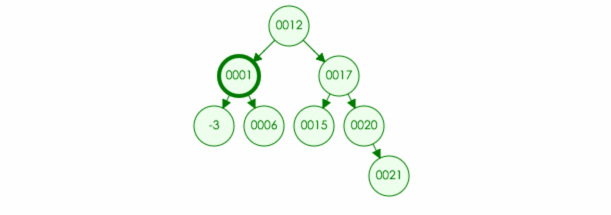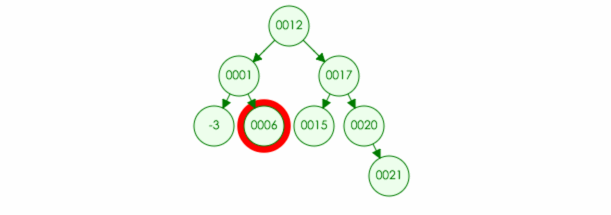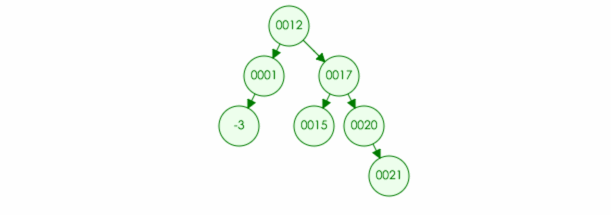
1.如果找不到该节点，那么什么都不用做

例如：要在树中删除元素 22

tree-delete-element-1.gif

2.如果被移除的元素在叶节点(no children)：那么直接移除该节点，并且将父节点原本指向该位置改为 null (如果是根节点，那就不用修改父节点指向位置)

例如：要在树中删除元素 6

tree-delete-element-2.gif

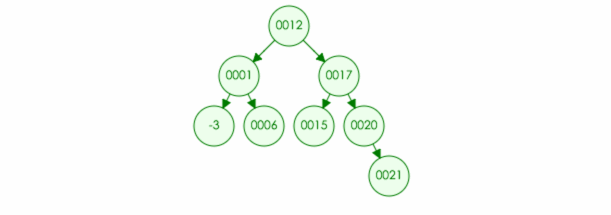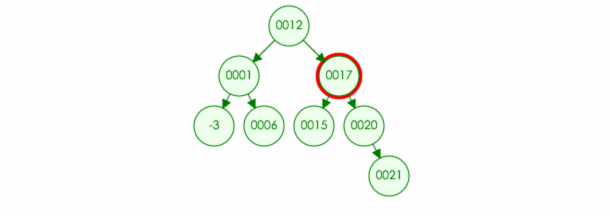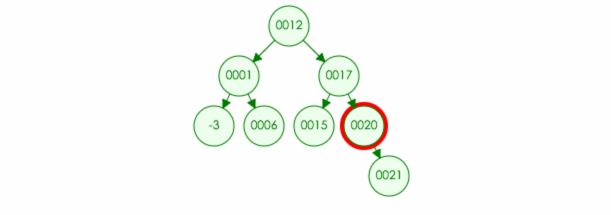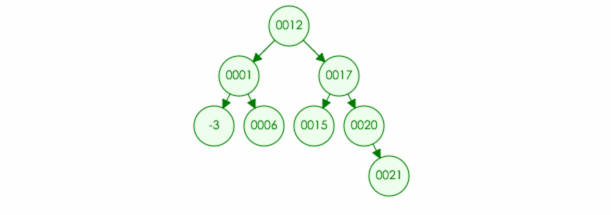
3.如果删除的元素只有一个儿子(one child)：那么也很简单，直接删除该节点，并且将父节点原本指向的位置改为该儿子 (如果是根节点，那么该儿子成为新的根节点)

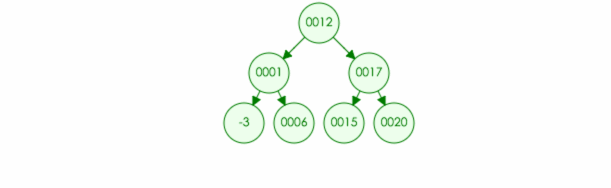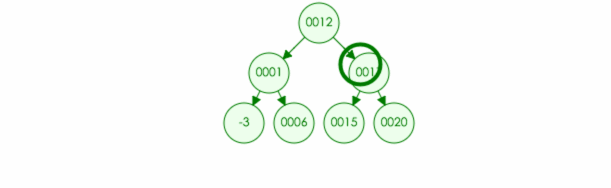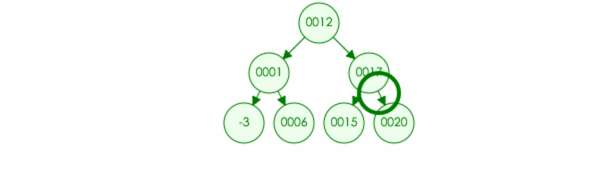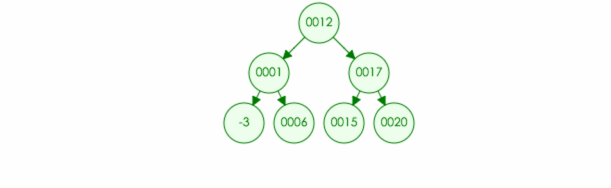
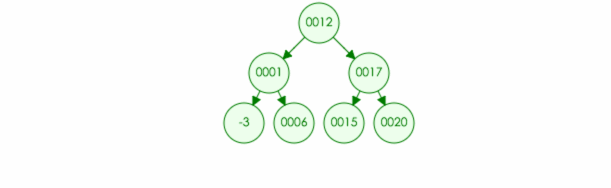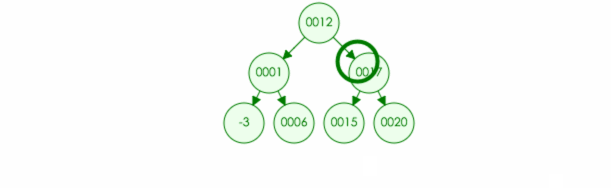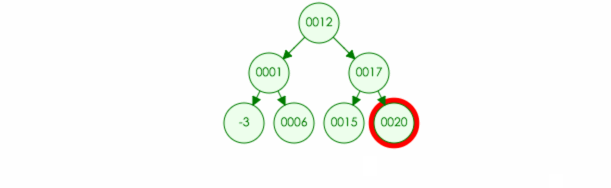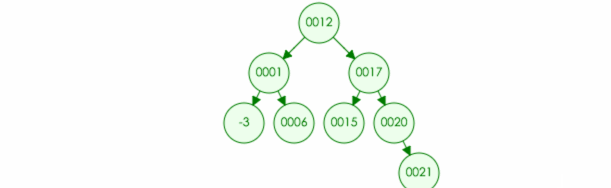
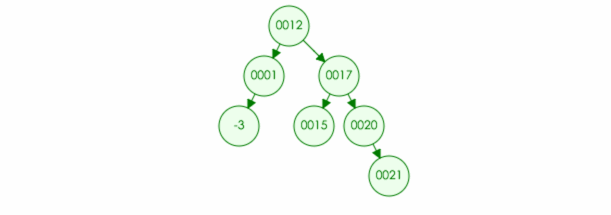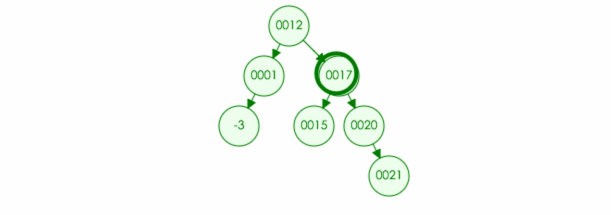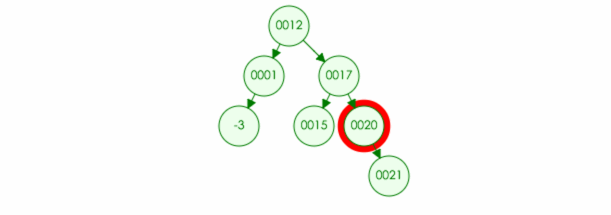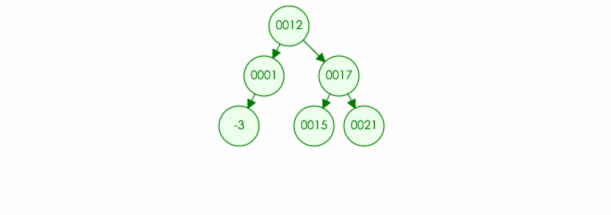
例如：要在树中删除元素 20

tree-delete-element-3.gif

4.如果删除的元素有两个儿子，那么可以取左子树中最大元素或者右子树中最小元素进行替换，然后将最大元素最小元素原位置置空

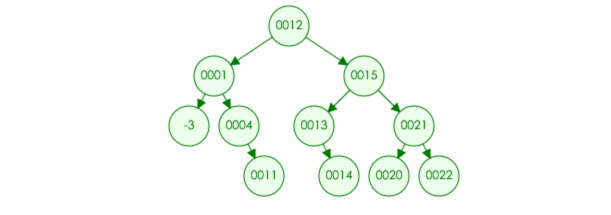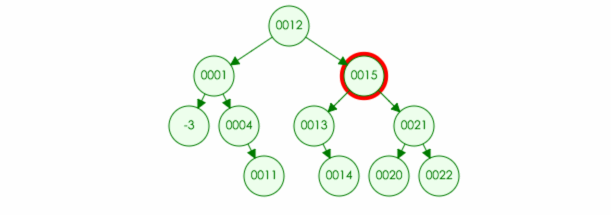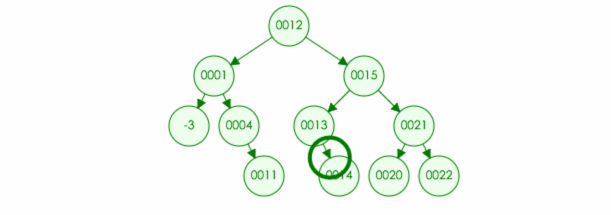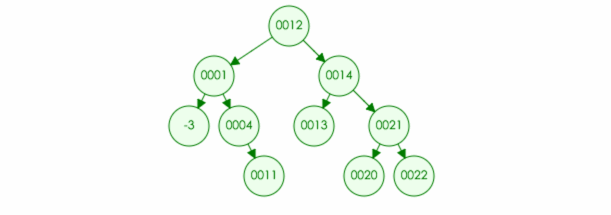
例如：要在树中删除元素 15

tree-delete-element-4.gif

平衡树的应用：

1. 排序：我们可以将数据一个个读取，构造出一棵平衡树。但我们读取完所有数据后，我们可以按次序遍历该树。但是在插入的过程中需要不断调整。否则他有可能会越来与不平衡，调整的方式有我们后面介绍的 AVL 树和红黑树两种方法。
2. 时间复杂度为 O(nlog2n + n)
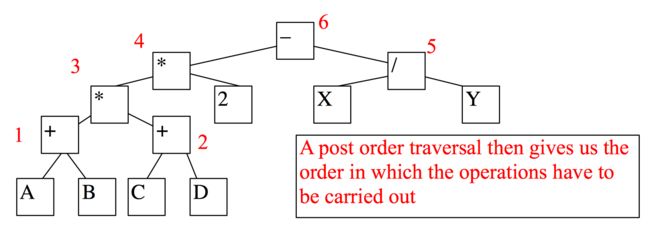
3. 编译算数表达式：
   我们可以将算术表达式展现为一棵搜索树：所有的叶子节点都是常量或者变量，而除叶节点外所有节点都是操作符。

比如：我们可以将 (A + B) * (C + D) * 2 - X / Y展现为

post order.png

(七) 平衡树 (Balanced Tree)

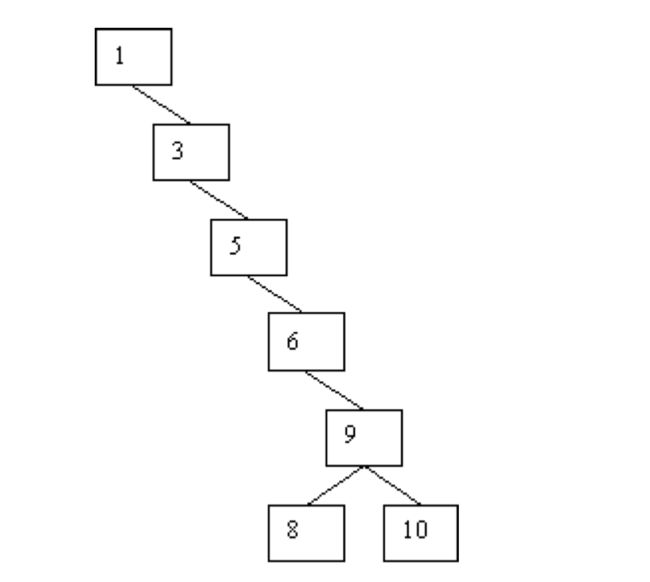
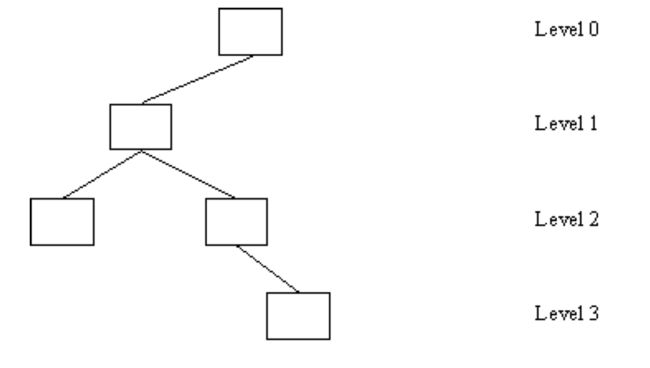
二叉搜索树虽然在插入和删除时的效率都有所提升，但是如果二叉树变成了下图：

LinkList.png

二叉树快退化成了，那么搜索效率效率就会变得很低,时间复杂度由 logn 退化到 n，这时候我们需要添加一些额外的条件来约束它，使其可以保持具有 logn 的时间复杂度。

老师上课讲的平衡树跟我在网上搜到的绝大部分平衡树都不一样，网上介绍的平衡树就是 AVL 树，而老师介绍的则是另一种平衡树，这里我以老师介绍的为主。

首先平衡树得是二叉树，它满足二叉树的所有性质。

判定是否为平衡树的条件：将该树重新排序，若不存在重新排序后的二叉树的树高比原来的树小，则判定该树为平衡树。

比如:

balanced-tree.png

这里有棵树高度为 2，那么我们知道高度为 1 的树最多只有三个节点，五个节点是无法构成一棵高度为 1 的二叉树，故上图的二叉树是平衡树。

又比如：

no-balanced-tree.png

该树高度为 3，我们知道一棵高度为 2 的树最多可以有 2^(h + 1) - 1 = 7(满二叉树)的节点，故图上的的树只有五个节点，那么它经过重新调整之后可以变为一个高度为 2 的二叉树，故不符合平衡树的性质，故该树不是平衡树。

由上我们可以得出一个结论：

1. 如果一棵树是平衡的，那么它所满足的节点数 n 需要满足 2^h - 1 < n <= 2^(h + 1) - 1
2. 插入和删除一个节点的时间复杂度均为: O(logn)
3. 这里虽然有一些算法可以使平衡二叉树 - 但是它们并没什么卵用，因为我们一般都是在添加或删除操作时候来去平衡树，而不是再一开始去平衡树。