深入 NumPy 模块
# 来源:NumPy Biginner's Guide 2e ch6
矩阵的逆
import numpy as np
A = np.mat("0 1 2;1 0 3;4 -3 8")
print "A\n", A
'''
A
[[ 0 1 2]
[ 1 0 3]
[ 4 -3 8]]
'''
# 求解矩阵的逆,不可逆会报错
inverse = np.linalg.inv(A)
print "inverse of A\n", inverse
'''
inverse of A
[[-4.5 7. -1.5]
[-2. 4. -1. ]
[ 1.5 -2. 0.5]]
'''
print "Check\n", A * inverse
'''
Check
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
'''
求解线性方程组
import numpy as np
A = np.mat("1 -2 1;0 2 -8;-4 5 9")
print "A\n", A
'''
A
[[ 1 -2 1]
[ 0 2 -8]
[-4 5 9]]
'''
b = np.array([0, 8, -9])
print "b\n", b
'''
b
[ 0 8 -9]
'''
# solve 求出向量 x,使 Ax = b
# 内部使用 np.dot(A.I, b) 来计算
# 所以 A 不可逆时报错
x = np.linalg.solve(A, b)
print "Solution", x
'''
Solution [ 29. 16. 3.]
'''
print "Check\n", np.dot(A , x)
'''
Check
[[ 0. 8. -9.]]
'''
特征值和特征向量
# 如果 Ax = λx,并且 x 非零
# 则 λ 是 A 的特征值,x 是 A 关于 λ 的特征向量
import numpy as np
A = np.mat("3 -2;1 0")
print "A\n", A
'''
A
[[ 3 -2]
[ 1 0]]
'''
# eigvals 仅仅求解特征值
print "Eigenvalues", np.linalg.eigvals(A)
# Eigenvalues [ 2. 1.]
# eig 求解特征值和特征向量
# 特征向量是数组的列
eigenvalues, eigenvectors = np.linalg.eig(A)
print "First tuple of eig", eigenvalues
print "Second tuple of eig\n", eigenvectors
'''
First tuple of eig [ 2. 1.]
Second tuple of eig
[[ 0.89442719 0.70710678]
[ 0.4472136 0.70710678]]
'''
for i in range(len(eigenvalues)):
print "Left", np.dot(A, eigenvectors[:,i])
print "Right", eigenvalues[i] * eigenvectors[:,i]
print
'''
Left [[ 1.78885438]
[ 0.89442719]]
Right [[ 1.78885438]
[ 0.89442719]]
Left [[ 0.70710678]
[ 0.70710678]]
Right [[ 0.70710678]
[ 0.70710678]]
'''
奇异值分解
# 奇异值是 A * A.T 特征值的算术平方根
# 若 A 是 mxn 阶矩阵
# 奇异值分解将 A 分解成 USV
# U 是 mxm 阶。S 是 mxm 阶对角矩阵,由奇异值构成
# V 是 mxn 阶
import numpy as np
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
'''
A
[[ 4 11 14]
[ 8 7 -2]]
'''
# linalg.svd 求解奇异值
U, Sigma, V = np.linalg.svd(A, full_matrices=False)
print "U"
print U
'''
U
[[-0.9486833 -0.31622777]
[-0.31622777 0.9486833 ]]
'''
print "Sigma"
print Sigma
'''
Sigma
[ 18.97366596 9.48683298]
'''
print "V"
print V
'''
V
[[-0.33333333 -0.66666667 -0.66666667]
[ 0.66666667 0.33333333 -0.66666667]]
'''
print "Product\n", U * np.diag(Sigma) * V
'''
Product
[[ 4. 11. 14.]
[ 8. 7. -2.]]
'''
print np.linalg.eigvals(A * A.T) ** 0.5
'''
[ 18.97366596 9.48683298]
'''
广义逆矩阵
# 若存在唯一矩阵 M,满足
# AMA = A,MAM = M,AM 和 MA 均为对称矩阵
# 则 M 是 A 的广义逆矩阵
import numpy as np
A = np.mat("4 11 14;8 7 -2")
print "A\n", A
'''
A
[[ 4 11 14]
[ 8 7 -2]]
'''
# linalg.pinv 求解广义逆
pseudoinv = np.linalg.pinv(A)
print "Pseudo inverse\n", pseudoinv
'''
Pseudo inverse
[[-0.00555556 0.07222222]
[ 0.02222222 0.04444444]
[ 0.05555556 -0.05555556]]
'''
print "Check", A * pseudoinv
'''
Check [[ 1.00000000e+00 0.00000000e+00]
[ 8.32667268e-17 1.00000000e+00]]
'''
计算矩阵行列式
import numpy as np
A = np.mat("3 4;5 6")
print "A\n", A
'''
A
[[ 3. 4.]
[ 5. 6.]]
'''
# linalg.det 求解行列式
# 对于二阶矩阵
# det(A) = A[0][0] * A[1][1] - A[0][1] * A[1][0]
print "Determinant", np.linalg.det(A)
# Determinant -2.0
快速傅里叶变换(FFT)
import numpy as np
from matplotlib.pyplot import plot, show
# 创建 30 个点的余弦波
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
# 使用 fft 函数变换余弦波
transformed = np.fft.fft(wave)
# 验证是否能够还原数据
print np.all(np.abs(np.fft.ifft(transformed) - wave) < 10 ** -9)
# True
# 绘制变换后的信号
plot(transformed)
show()
调整频率
import numpy as np
from matplotlib.pyplot import plot, show
# 创建 30 个点的余弦波
x = np.linspace(0, 2 * np.pi, 30)
wave = np.cos(x)
# 使用 fft 函数变换余弦波
transformed = np.fft.fft(wave)
# 使用 fftshift 函数调整信号
shifted = np.fft.fftshift(transformed)
# 检查是否可以还原
print np.all(np.abs(np.fft.ifftshift(shifted) - transformed) < 10 ** -9)
# 绘制信号
plot(transformed, lw=2)
plot(shifted, lw=3)
show()
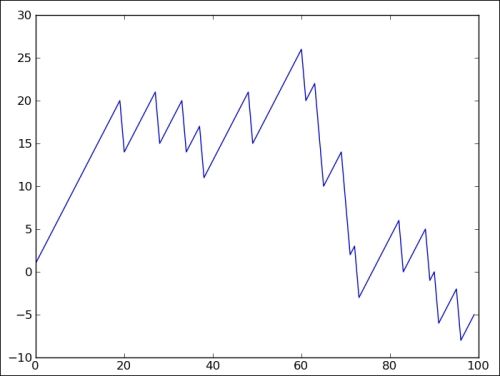
随机游走
import numpy as np
from matplotlib.pyplot import plot, show
# 创建大小为 10000 的余额数组
# 初始余额为 1000
cash = np.zeros(10000)
cash[0] = 1000
# 生成随机数,其概率满足二项分布 B(n = 9, p = 0.5)
# P(x = k) = C(n, k) * p ** k * (1 - p) ** (n - k)
# x: 0 ~ 9
outcome = np.random.binomial(9, 0.5, size=len(cash))
for i in range(1, len(cash)):
# 如果随机数小于 5,余额减一,否则加一
# p = 0.5 时,二项分布是对称的
# 所以小于 5 的概率应该是 0.5
if outcome[i] < 5:
cash[i] = cash[i - 1] - 1
elif outcome[i] < 10:
cash[i] = cash[i - 1] + 1
else:
raise AssertionError("Unexpected outcome " + outcome)
print outcome.min(), outcome.max()
# 0 9
# 绘制余额变化情况
plot(np.arange(len(cash)), cash)
show()
模拟游戏节目
# 游戏节目中有一个桶,里面有 25 个正常球
# 和一个倒霉球
# 选手正确回答问题后都需要取出三个球
# 如果三个都是普通球,分数加一
# 否则分数减六
import numpy as np
from matplotlib.pyplot import plot, show
# 创建分数数组
points = np.zeros(100)
# hypergeometric 函数生成的随机数满足超几何分布
# 超几何分布描述了,袋子里有两类球,从袋子里取出几个球,取到 k 个一类球的概率。
# 参数分别为:普通球的个数,倒霉球的个数,取出的个数
# 随机数模拟了取出的球中普通球的个数
outcomes = np.random.hypergeometric(25, 1, 3, size=len(points))
for i in range(len(points)):
if outcomes[i] == 3:
# 如果三个都是普通球,分数加一
points[i] = points[i - 1] + 1
elif outcomes[i] == 2:
# 如果存在倒霉球,分数减六
points[i] = points[i - 1] - 6
else:
print outcomes[i]
# 绘制分数变化情况
plot(np.arange(len(points)), points)
show()
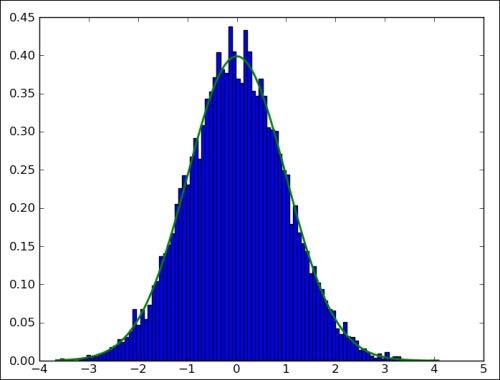
绘制正态分布
import numpy as np
import matplotlib.pyplot as plt
N=10000
# 生成随机数,其概率满足正态分布 N(mu = 0, sigma = 1)
normal_values = np.random.normal(size=N)
# 绘制直方图,横轴是分组,纵轴是出现频率
# 第二个参数表示 100 个组(默认 10 个)
# bins 是组中值
dummy, bins, dummy = plt.hist(normal_values, np.sqrt(N), normed=True, lw=1)
# 绘制正态分布概率密度函数
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()
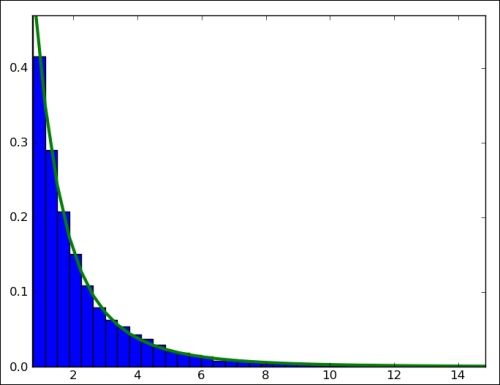
绘制对数正态分布
# 和上一段代码基本一样
import numpy as np
import matplotlib.pyplot as plt
N=10000
# 将这里改成 lognormal 来生成对数正态分布的随机数
lognormal_values = np.random.lognormal(size=N)
dummy, bins, dummy = plt.hist(lognormal_values, np.sqrt(N), normed=True, lw=1)
sigma = 1
mu = 0
x = np.linspace(min(bins), max(bins), len(bins))
# 修改这里的公式
pdf = np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))/ (x * sigma * np.sqrt(2 * np.pi))
plt.plot(x, pdf,lw=3)
plt.show()