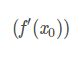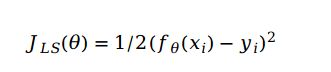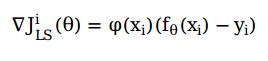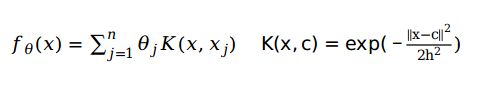什么是梯度
在微积分里,对多元函数参数求导数,把求得各个参数以向量的形式写出来,这就是梯度。在几何意义中,梯度就是函数变化的快慢。沿着梯度向量的方向更容易找到最大值,沿向量相反的方向,更容易找到函数的最小值。
最简单的对于一元函数来说,一元函数y=f(x)在点x0处的梯度:
这就是最简单的梯度,记为gradf。
将上面一元二次函数求导,在极小值左边的导数为负数,梯度向量就是指向左边的一维向量,所以参数Theta沿着梯度方向往左走,函数值就会增大,反之同理!
梯度下降法
梯度下降的直观解释就是:比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是每走到一个位置的时候,求解当前未知的梯度,沿着梯度负方向走下一步,然后继续求解当前位置梯度,一步一步走下去,直到我们走到山底,但是这也可能走到一个局部的山峰低处(类似于盆地的意思)。
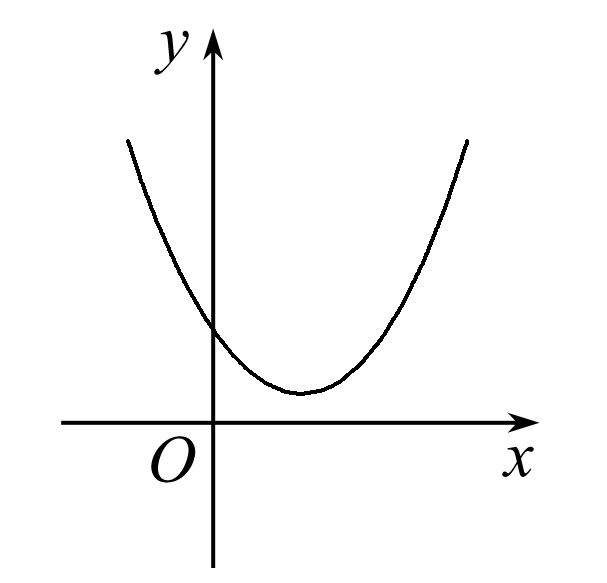
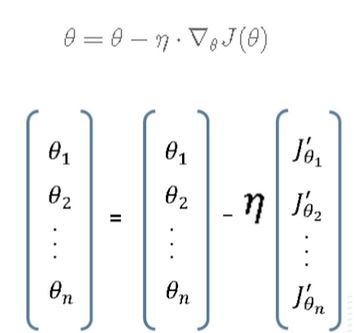
梯度下降法公式如下图所示:
对于公式,通过控制步伐的大小来控制一步步迭代到极小值处,迭代方向为当前位置负梯度方向,步伐则由学习率来控制。
J()就是我们采用的最小二乘法。
对J()求导,得到
实例讲解
首先假定一个模型为y=2x,保存几组训练集,例如(1,1),(2,4)。然后给定一个初始值Theta=1.
采用梯度下降的方法,设方程为y=Theta*x,即:y=x。
随机给定一个x,然后求出梯度方向。
根据最小二乘的公式得出J()。
根据梯度下降法(学习率自己设定)得出下一个Theta。
通过迭代次数最终趋于收敛,这时候的Theta就是最优的Theta!
例如下面代码:
import numpy as np
import matplotlib.pyplot as plt
import math
import random
X0 = np.ones((100, 1))
X1 = np.random.random(100).reshape(100,1)
X = np.hstack((X0,X1))
y = np.zeros(100).reshape(100,1)
for i , x in enumerate(X1):
val = x*2+1+random.uniform(-0.2,0.2)
y[i] = val
def gradientDescent(X,y,times = 10000, alpha=0.01):
'''
alpha:学习率,默认0.01
times:迭代次数,默认1000次
'''
m = len(y)
theta = np.array([1,1]).reshape(2, 1)
loss = {}
for i in range(times):
diff = np.dot(X,theta)- y
#cost = (diff**2).sum()/(2.0*m)
#loss[i] = cost
theta = theta - alpha*(np.dot(np.transpose(X), diff)/m)
#plt.figure(figsize=(8,6))
#plt.scatter(loss.keys(),loss.values(),color='r')
#plt.show()
return theta
theta = gradientDescent(X,y)
plt.figure(figsize=(8,6))
plt.scatter(X1,y,color='g')
plt.plot(X1,X1*2+1,color='r',linewidth=2.5,linestyle='-')
plt.plot(X1,np.dot(X,theta),color='b')
plt.show()
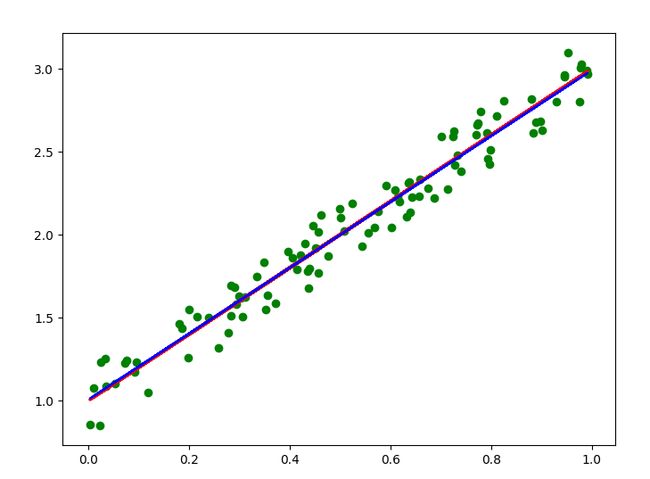
最后拟合图像如下图:
其中红色是设置的函数,蓝色是拟合图像,这两个函数基本吻合,说明拟合情况较好。
现在我们采用梯度下降的方法对sin(pix)/pix+0.1pix+0.1*随机数(加入噪点),对这个函数进行学习。
这里采用的是高斯核函数模型,对于高斯核模型,如下:
代码实现:
首先定义一个函数,,返回值为上述函数的y值
def fun0(x):
pix=math.pi*x
return np.sin(pix)/pix+0.1*pix+0.1*np.random.rand()
在某个范围内定义一定数量的点,得出上述函数的y值并存在一个矩阵中
n=50
x=np.linspace(-3,3,n)
y=np.array(list(map(fun0,x)))
现在训练样本就已经准备完毕了。接下来进行训练!
首先取一个随机数(0-50之内的一个整数),通过高斯核函数求得高斯核函数的值
通过梯度下降法求得下一时刻的Theta值
训练多次之后得出最优的Theta值
输出拟合图像。
代码如下如所示:
import numpy as np
import matplotlib.pyplot as plt
import math
n=50
N=1000
x=np.linspace(-3,3,n)
X=np.linspace(-3,3,N)
def fun0(x):
pix=math.pi*x
return np.sin(pix)/pix+0.1*pix+0.1*np.random.rand()
'''def fun1(x):
f=x
return f '''
y=np.array(list(map(fun0,x)))
hh=2*pow(0.3,2)
t0=np.random.randn(n)
alpha=0.1
xs=x[0:int(n)]
def K(xi):
K=[]
for a in range(len(xs)):
K.append(math.exp(-(xi-xs[a])**2/hh))
return np.array(K)
for o in range(1000):
i=math.ceil(np.random.rand()*(n-1))
k=K(x[i])
t=t0-alpha*k*(np.dot(k,t0)-y[i])
#sh = np.dot(x,t0).reshape(50,1)-y
#ss=np.dot(np.transpose(x),sh)
#print(sh.shape[:])
#t=t0-alpha*(ss)/50
#print(t0.shape[:])
#print(t.shape[:])
if np.linalg.norm(t-t0)<0.000001:
break
t0 = t
def fun(Xi):
return K(Xi).dot(t0.reshape((-1,1)))
#print(t0)
#Y= np.dot(X,t0)
Y=np.array(list(map(fun,X))).reshape((-1,))
error=np.array(list(map(fun,x))).reshape((-1,))-y
plt.plot(x,y,'g.') #绘制样本点
plt.plot(X,Y,'r-') #绘制拟合曲线
plt.plot(x,error,'b-') #绘制样本点拟合误差
plt.show()
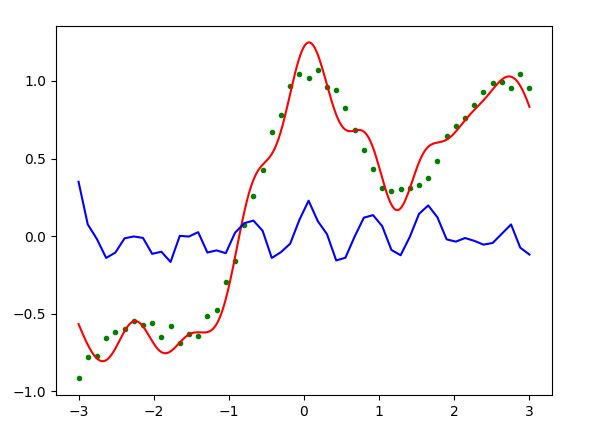
拟合曲线如下图所示: