关于FFT快速傅氏变换的理解
FFT(Fast Fourier
Transformation)是离散傅氏变换(DFT)的快速算法。即为快速傅氏变换。
傅里叶变换大致有四种类型:
(1)连续傅里叶变换(FT)
(2)连续傅里叶级数(FS)
(3)离散时间傅里叶变换(DTFT)
(4)离散傅里叶级数(DFS)
这里主要讲解离散时间傅里叶变换中的一种快速变换算法FFT,适用于计算机,微处理器等数字设备进行运算分析。
提到傅里叶变换,畏难心理可能让大多数人都觉得很难,要么在门外不敢踏进来看看,要么就是进来后深陷傅氏复杂枯燥无味的理论而无法自拔,最后过段时间什么也不记得了。这是由于大家没有真正将傅氏变换应用起来,一直处于理论分析层次,不免让人觉得傅氏很高冷。其实真正的傅氏是很接地气的,很有用,应用范围非常广泛。这里主要结合Matlab仿真通过例子详细分析FFT的使用。
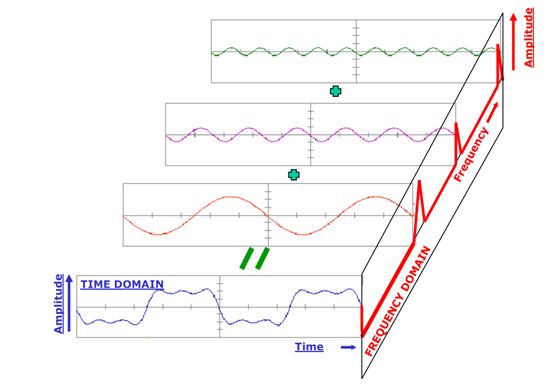
FFT是将离散的时间域信号变换到频域内进行分析。主要应用于对信号的提取和分析,去噪。如图所示:用一首古诗形容FFT存在的意义最贴切了:横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。有时候我们在时域中对一个有用的信号提取我们需要的有效成分,剔除噪声是很困难的,信号和噪声杂糅在一起,根本无法区分开,如果我们在频域中分析信号和噪声就容易多了,信号的幅值一般比噪声幅值大很多,噪声幅值较小,在频域中,噪声无处遁形,根据频域幅值纵坐标可以发现我们需要的信号,再通过频率横坐标就可以知道有用信号的频率范围了,整个去噪过程就是这么简单。
FFT中关键的参数:采样频率:fs; //根据奈奎斯特采样定理(又称香农采样定理):fs≥2fmax
采样点数:N; //N个点(0:N-1),频域中横坐标有效数据范围(0:N-1)
采样频率分辨率:fs_div=fs/N; //频域中,横坐标的分辨率(最小刻度)
采样周期(采样频率分辨率的倒数,也是采样频率fs倒数与采样点数N的乘积):Ts=1/fs_div=N/fs; //一个周期采样N个点
由上面公式可知采样频率分辨率fs_div和采样周期Ts有关(也就是和采样频率fs,采样点数N共同决定的),采样周期Ts越长,采样频率分辨率fs_div值越小,分辨率就越高。(1)当采样频率fs保持不变时,增大采样点数N,采样频率分辨率fs_div值变小,分辨率就变高。
(2)当采样点数N保持不变时,减小采样频率fs,采样频率分辨率fs_div值变小,分辨率就变高。(前提要保证采样定理,否则减小采样频率也就失去了意义,采集的数据已经失真,失去了应有的价值了)
举例介绍FFT的使用:
例程1:clf;
x=[2,5,1,9,10,2];
y=fft(x);
y=
29.0000 + 0.0000i -9.0000 + 5.1962i 2.0000 -10.3923i -3.0000 + 0.0000i 2.0000 +10.3923i -9.0000 - 5.1962i
对矩阵x进行FFT变换,得到的八个分量,第一个为直流分量29,其余的分量按照实轴对称分布。
例程2:y1=8*sin(2*pi*15*t)+16*sin(2*pi*30*t)。采样频率fs=128Hz,分别绘制N=128、1024点幅频图。fs>2*fmax(即30),满足采样定理。
clf;
fs=128;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列
y1=8*sin(2*pi*15*t)+16*sin(2*pi*30*t); %信号
y=fft(y1,N); %对信号进行快速Fourier变换
mag=abs(y); %求得Fourier变换后的振幅
f=n*fs/N; %频率序列
subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('fs=128 N=128');grid on;
subplot(2,2,2),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('fs=128 N=128');grid on;
%对信号采样数据为1024点的处理
fs=128;N=1024;n=0:N-1;t=n/fs;
y1=8*sin(2*pi*15*t)+16*sin(2*pi*30*t); %信号
y=fft(y1,N); %对信号进行快速Fourier变换
mag=abs(y); %求取Fourier变换的振幅
f=n*fs/N;
subplot(2,2,3),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('fs=128 N=1024');grid on;
subplot(2,2,4)
plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('fs=128 N=1024');grid on;
%得到的频域图,信号的幅值变换为实际大小:需乘以2除以N(采样点数)%得到的频域图,信号的幅值变换为实际大小:需乘以2除以N(采样点数)
整个频谱图是以Nyquist频率(fs/2)为对称轴的
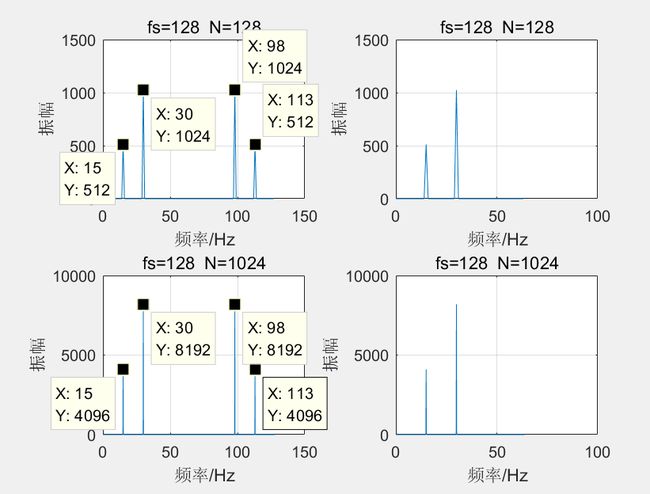
由上图可以看出信号中的两种频率信号:15HZ,30HZ。直接在时域中看原始信号是没有办法得到有用信号的。只有换个视角,从频域看才能得到我们想要的信号量。
幅值计算:(1)fs=128,N=128,频率为15HZ的信号幅值A=512*(2/N)=8,由信号组成y1=8*sin(2*pi*15*t)+16*sin(2*pi*30*t)可以看出15HZ信号的幅值为8。(2)fs=128,N=128,频率为30HZ的信号幅值A=1024*(2/N)=16,符合实际结果。(3)fs=128,N=1024,频率为15HZ的信号幅值A=4096*(2/N)=8,符合实际结果。(4)fs=128,N=1024,频率为30HZ的信号幅值A=8192*(2/N)=16,符合实际结果。
我的博客:https://blog.csdn.net/Usain_Bolt_