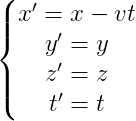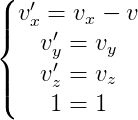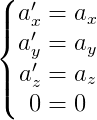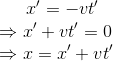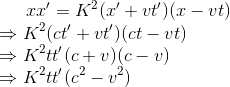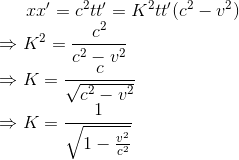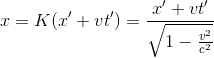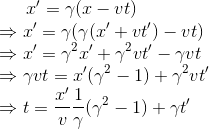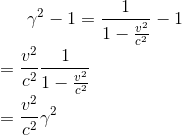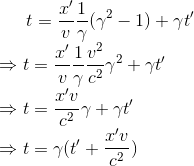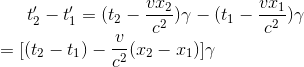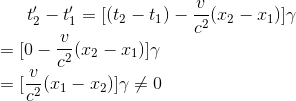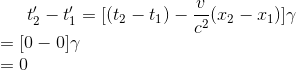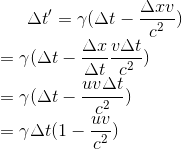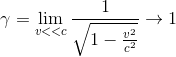本章涉及知识点
1、伽利略变换的数学推导
2、狭义相对论的两个基本假设
3、洛伦兹变换的数学推导
4、狭义相对论的时空观
5、狭义相对论的数学分类讨论
6、狭义相对论案例的求解分析
7、python编程来求解案例
一、伽利略变换的数学推导
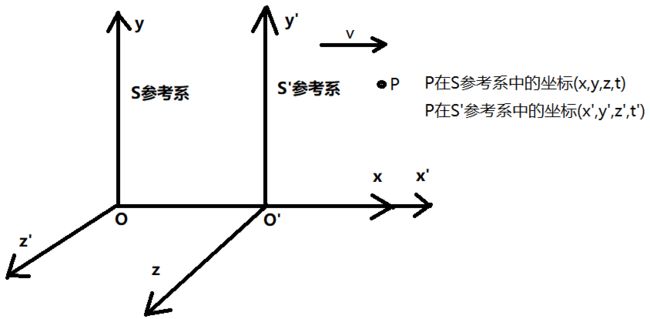
在引入相对论之前,我们必须先要了解牛顿经典力学的支柱—伽利略变化。该理论中,牛顿和伽利略认为空间是独立的,与参考系中物体的运动状态无关,且时间是均匀流逝的
即伽利略的时空变化是:空间和时间都是绝对的
如下图实验所示
其中S和S'是两个惯性参考系,对任意事件P在S和S'中的坐标分别为(x,y,z,t)和(x',y',z',t'),显然,我们要研究的时空关系,即是研究空间变化(x和x'、y和y'、z和z'这三个方向),以及时间变化(t和t')的关系即可。我们假设S'相对于S以平行于x轴的速度v做匀速运动
研究的事件为:以两个参考系的坐标原点O和O'重合为计时起点,经过时间t后两个参考系观察到S系原点的位置关系?
由于我们推导是的伽利略变换,时间是绝对的,所以我们可以得到时间的变化关系为
上面的方程式说明,时间是不受观察者所在参考系的运动状态影响,即时间是绝对的
下面我们来看两个参考系的空间关系,由于运动只发生在x轴,所以我们可以得到y轴和z轴的空间变化关系为
当在S系中观察S系的原点时,S系的x轴关系为
而在S'系中观察该点时,S'系的x轴关系为
我们将上面两个式子整合为
经过上面分析,我们得到了伽利略变换的时空数学方程表达式为
我们对上面的方程式中的每个式子对时间t求导数,可以得到速度变化为
我们在对上面的方程式中的每个式子对时间t求导数,可以得到加速度的变化为
可以看到,在S参考系中牛顿力学F=ma,则在S'参考系中F=ma'也成立,所以伽利略变换是牛顿经典力学的基础
但是在狭义相对论中,爱因斯坦却认为时间和空间是相对的,并不是绝对的!现代物理学中电、光、磁现象也是符合相对性原理的,即时间和空间的关系和伽利略变换发生了严重的矛盾冲突,故而我们需要一套新的数学方程组,来调和牛顿的经典力学和爱因斯坦的狭义相对论,而洛伦兹变换就是做这件事的
二、狭义相对论的两个基本假设
在推导洛伦兹变化之前,我们需要知道狭义相对论的两个基本假设
(1)相对性原理:一切物理定律的方程式在洛伦兹变化下,依旧保持其数学形式
(2)光速不变原理:在所有惯性坐标系中,真空中的光速保持不变,且光速c是物质的极限速度
有了上面两个基本假设,接下来我们就可以推导洛伦兹变化
三、洛伦兹变换的数学推导
仍然以推导伽利略变化的实验来研究,首选我们需要认清一个事实,时间不是绝对的!所以在S和S'参考系中,时间的关系也是相对的,即
这个方程非常重要,这也说明了我们不能从绝对时间出发来推导空间关系,因为时间是相对的
同理,因为运动只发生在x轴,所以我们也可以得到y轴和z轴的空间变化关系为
当在S系中观察S系的原点时,S系的x轴关系为
而在S'系中观察该点时,S'系的x轴关系为
注意上式中右侧是t'(要和伽利略变化推导区分开),我们整合两个式子为
由于我们认为时间和空间是均匀的,即时空坐标的变化是线性的,因此我们设K是一个比例常数,可以得到S参考系中任意一个点的空间x坐标为
同理设K'是一个比例常数,我们也可以得到S'参考系中任意一个点的空间x'坐标为
由狭义相对论的第一条相对性假设,惯性坐标系S和S'的数学表达式一致,即二者是等价的,则可以得到比例阐述K和K'的关系为
下面我们需要求解出这个常数K,此时我们还需要一组方程组,由义相对论的第二条光速不变原理,同理我们假设光信号在S系和S'系的原点重合处开始计时,在任意一个时刻沿着x轴前进,则光信号到达S和S'系中的位置横坐标分别为
上面方程式中的c代表着光速,根据狭义相对论的第二个假设,c不受所在坐标系的运动状态影响,它是一个常数,是任意物质速度的极限,则我们将上面两个关于c的方程式左右相乘得到
我们将S系和S'系中的横坐标(x和x')的表达式也左右相乘得到
我们将上式中的x和x'用ct和ct'带入整理得
联立x和x'的两个表达式,得
至此我们就求出了常数K的表达式,并且由上面的数学推导中可以看出,要保证分母不能为0,且根号里表达式非负,即满足
这个不等式约束条件说明了光速c是任何物体的极限速度
我们带入K的表达式,就可以得到x和x'的洛伦兹数学方程为
为了方便以后的推导,我们设r为
我们称r为洛伦兹因子,可以看到r只与坐标系的运动速度v和光速c有关,是一个常量,则关于S和S'的位置横坐标变化的数学方程可以写为
下面我们联立x和x'的洛伦兹数学方程,来带入消元分别求解洛伦兹时间的变化方程
消去x得到关于t的变化方程为
我们带入r计算出右边括号里的第一项结果为
带入右边第一项括号的计算结果,继续化简t的洛伦兹变化方程为
同上面的解方程方法,我们消去x'就可以得到关于t'的洛伦兹变化方程为
至此,我们以狭义相对论的两个基本假设为基石,通过求解方程租的方法,推导出了两个参考系之间关于时间空间变化的数学关系—洛伦兹变化方程(洛伦兹时空数学方程)
从这组方程可以明显的看出,时间不在是绝对的,而是相对的,时间已经和所处世界的运动状态产生了联系,同时洛伦兹变化也是狭义相对论的基本方程组
四、狭义相对论的时空观
有了以上关于洛伦兹变化的推导,狭义相对论的时空观认为:同时是相对的
即在一个惯性坐标系中,不同地点同时发生的两件事情,在另外一个惯性坐标系中不一定是同时的!
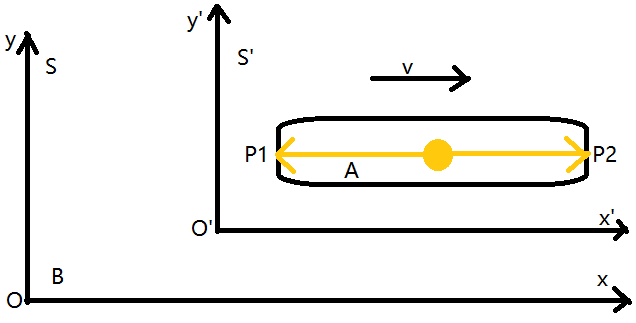
考虑一个实验,S'为一列高速运动的列车,S为列车站台,有AB两个观察员,A站在列车里跟随列车一起运动,B站在站台上,列车的天花板上偶遇一盏关闭的吊灯,AB观察员做同一件事情:同时记录打开吊灯后,光线照射到车厢左右两边的时间,如下图所示
我们设光线照射到列车左侧的事件为P1,照射到列车右侧的事件为P2,根据实验要求,AB观察员要同时测量吊灯打开后P1和P2发生的时间关系?
(1)对于观察者A:他的参考系为S',则A,吊灯都是相对于列车静止的,则P1事件和P2事件都是同时到达,即P1消耗的时间 = P2消耗的时间
(2)对于观察者B:他的参考系为S,则吊灯是运动的且运动状态和S'一致,由于光源射向列车左侧(P1事件)的方向与列车的运动相反,而射向列车右侧(P2事件)的方向与列车的运动相同,由光速不变的原理,光线会先到达左侧,再到达右侧,即P1消耗的时间
为此,我们得出一个结论:同时性与参考系的运动有关,即同时是相对的
下面我们用数学方法的推导,来证明这个结论
五、狭义相对论的数学分类讨论
假设有两个事件P1和P2,在S参考系中的时空坐标为
在S'参考系中的时空坐标为
由伦伦兹方程得到事件P1在S和S'参考系中发生的时间关系为
由伦伦兹方程得到事件P2在S和S'参考系中发生的时间关系为
则在S和S'参考系中测得这两个事件发生的时间间隔为(t2' - t1')和(t2 - t1),它们的数学关系为
得到不同参考系下两个事件发生的时间间隔的数学方程后,我们需要分类讨论这个方程的可能情况
(1)如果:在S系中P1、P2同时刻发生,但在不同地点发生
上述讨论情况翻译为数学语言即为
带入时间间隔方程后,就可以得到在该情况下,S'参考系中发生P1和P2的时间间隔为
从上述推导的时间间隔方程中,我们可以得出结论:同样的两个事件P1P2,如果在参考系S下同时刻但不同地发生,那么在参考系S'下将不会是同时刻发生!
(2)如果:在S系中P1、P2同时刻发生,且同地点发生
上述讨论情况翻译为数学语言即为
同理,带入时间间隔方程后,就可以得到在该情况下,S'参考系中发生P1和P2的时间间隔为
从上述推导的时间间隔方程中,我们可以得出结论:同样的两个事件P1P2,如果在参考系S下同时刻且同地发生,那么在参考系S'下也是同时刻发生!
(3)讨论在参考系S下发生某个事件,则该事件在参考系S'中的因果关系
设在S参考系中,逻辑事件为:质点经过△t后,到达位置x+△x处
则由洛伦兹变化得到该质点在参考系S'下的时间方程为
在研究事件的因果关系顺序,即要分析不同参考系下事件的时间方程的符号,如果符号相同,则说明在不同参考系下,同一个事件发生的因果关系不变;如果符号不同,则说明在不同参考系下,同一个事件发生的因果关系会发生颠倒
下面设△x对时间△t的导数为u,即
整理质点在参考系S'下的时间方程为
由于c > u、c > v,则比较上式就得到不同参考系下同一个事件发生的因果关系为
从上述推导结果中,我们可以得出结论:在不同参考系下,同一个事件发生的时间方程符号是同号的,即事件的因果关系一致,事件的逻辑顺序不会发生颠倒
(4)当参考系S'的运动速度v远远达不到光速c时
上述讨论情况翻译为数学语言即为
由于上述不等式的限制,我们的洛伦兹因子将近似趋近于
则在S'参考系下的时间方程将趋近于
显然,上述方程结果就是伽利略变化方程!
从上述推导结果中,我们可以得出结论:当参考系S'运动的速度远远小于光速c时,洛伦兹时空方程就变为了伽利略时空方程,即此时回到了牛顿经典力学!(现实生活中大部分都是这种情况)
同时我们也可以得出另一个结论:洛伦兹方程是连接爱因斯坦狭义相对论和牛顿经典力学的桥梁!
六、狭义相对论案例的求解分析
推导完了狭义相对论中的洛伦兹变化,我们来看以下案例:
案例:在惯性坐标系S中,有两个事件同时发生,且在x方向上相距1000m,从另一个惯性坐标系S'中观察这两个事件在x方向上相距2000m,求在S'系测得这两个事件发生的时间间隔是多少?
显然,根据狭义相对论的时空观,同时具有相对性,且根据第五点的分析,同时不同地方生的两件事,在别的参考系观察,这两件事一定不是同时的,下面我们通过洛伦兹变化来求解这个问题
首先由洛伦兹方程得到这两件事件在参考系S'中x方向的距离间隔为
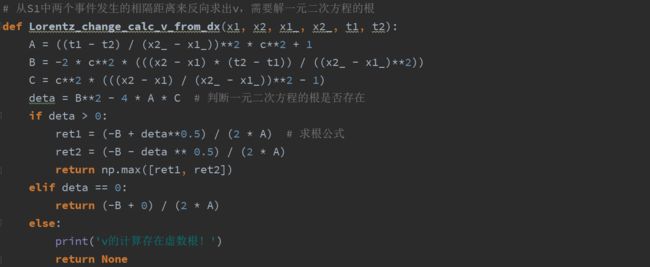
我们从这个方程中求解出S'坐标系的移动速度v,则需要用上式变化出v的方程式
可以看到参考系S'的运动速度v是一个关于变量v的二次函数,我们可以用二次函数的求根公式来求解v,注意既然是二次函数,我们就必须依据根的判别式来判断根的解情况
求解出v之后,我们用洛伦兹方程就可以求出这两个事件在参考系S'中观测的时间间隔为
七、python编程来求解案例
通过上述推导分析,我们将数学语言翻译成Python代码即可
洛伦兹方程计算在S'中两个事件发生的距离间隔:
洛伦兹方程计算在S'中两个事件发生的时间间隔
计算参考系S'的移动速度
初始化两个事件的各个条件为
求解案例的结果为
从结果中可以看到:当S'的运动速度达到光速的0.8倍时,S'系中的观察者观察到S系中的这两件事情发生的时间间隔大于0,说明这两件事在S'系中并不是同时发生的!(同时的相对性)
案例代码见:洛伦兹方程