LATEX 公式总结

在论文写作和博客中经常需要大量数学公式，latex可以帮助我们把数学公式完整的编辑出来，并作出优美的排版，我花了一些时间，综合一些博客和网络上的资料，做一个总结，方便自己查询使用
首先贴一个我常用的在线编辑网站，常见的数学符号都在上面
https://www.codecogs.com/latex/eqneditor.php?lang=zh-cn

虽然LaTex和Word都是非常完善的文本排版工具，但基于其数学公式编辑的便利，我这里着重讲解一下数学公式部分的应用，至于其他方面的应用，先跳过啦。

Markdown中的LaTeX格式

大部分情况下，我对于latex的数学公式都是内嵌于Markdown文本编辑器中的，分为两种形式

1. 行内公式排版：

$ c = \sqrt{a^{2}+b_{0}^{2}+e^{x}} $

2. 块公式排版：

$$ c = \sqrt{a^{2}+b_{0}^{2} +e^{x}} $$

LaTex的数学公式基本规则

1. 转义

以下几个字符: # $ % & ~ _ ^ \ { }有特殊意义，需要表示这些字符时，需要转义，即在每个字符前加上\（转义字符的具体含义下面会解释）

image.png

不知为何不支持~的表示，需要时写作\sim

\boxed命令给公式加一个方框。\fbox具有类似功能
\mathbf将字体加粗
\boldsymbol将字体斜体且加粗

$E = mc^2 $
$ \boxed{E=mc^2} $
$\fbox{E=mc^2}$
$\mathbf{E = mc^2}$
$\boldsymbol{E = mc^2}$

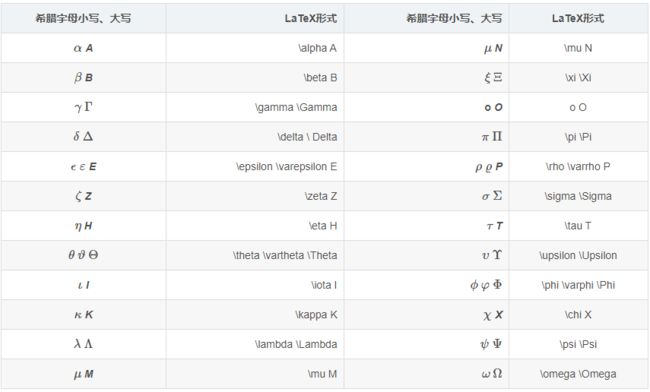
2. 希腊字母与特殊字符

image.png

image.png

image.png

3. 上下标及常用符号

用^来表示上标
用_来表示下标
根号用\sqrt表示

注意：这些有特殊含义的表示中（不限于这三种内容），如果超过一个字符或符号，需要用{}括起来。

对角标的使用中，如果角标位置看起来不明显时，可以强制改变角标大小或层次，如下所示：

$y_N, y_{_N},$

显示为：

第一种输出为正常输出，但输出效果不明显；第二种是将一级角标改为二级角标，字体也自动变为二级角标字体

当需要在左右两边都有上下标，可以用 \sideset 命令

$$ \sideset{^1_2}{^3_4}\bigotimes $$

\sqrt[开方次数，默认为2]{开方公式}， 例如：

$$ x_{k}^2\quad \sqrt{x}\quad \sqrt[3]{x+y} $$

公式中插入文本\text{}或\mbox{}，建议使用前者，它对于latex内置的\mbox{}的优势在于它可以根据当前位置自动调整文本样式（尤其是大小），而\mbox采用统一的正文样式。这一点在你的文本被用作上下标的时候非常重要。

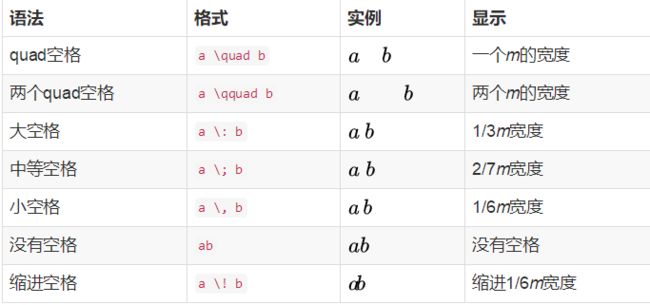
公式中插入空格，间隔效果如下表：

image.png

若需要显示更大或更小的字符，在符号前插入 \large 或 \small 命令

$A\large  A  \small A$

省略号\dots, \cdots,\vdots \ddots表示，\cdot常表示点乘，\vots是竖直方向的，\ddots是斜线方向的

$$ x_1, x_2, \dots, x_n\quad 1,2,\cdots,n\quad \vdots\quad \ddots $$

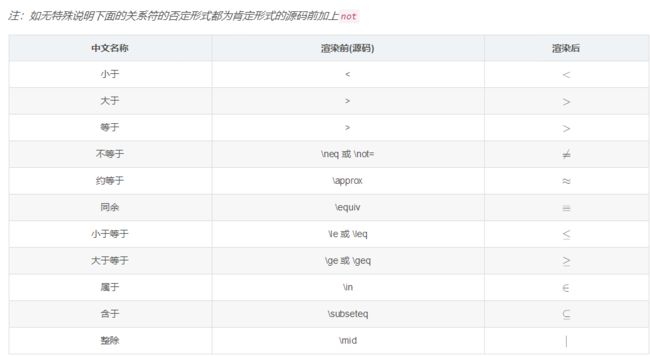
关系符如下表所示

image.png

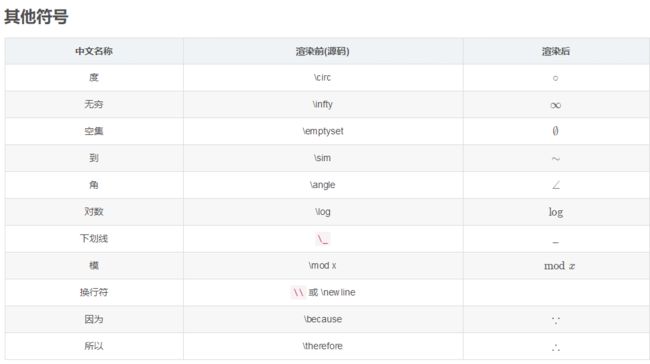
其他常用符号

image.png

4. 分数与组合数

分数用\frac{分子}{分母}表示，\cfrac用于连分数表示(这样相较于\frac不会产生字体自动缩小的问题)

$x = a _ 0 + \cfrac {1} {a _ 1
          + \cfrac {1} {a _ 2
          + \cfrac {1} {a _ 3 + \cfrac {1} {a _ 4} } } } 
$

字号工具环境设置：
\dfrac命令把字号设置为独立公式中的大小；
\tfrac则把字号设置为行间公式中的大小。

$ \frac{1}{2} \dfrac{1}{2} $ 

$$ \frac{1}{2} \tfrac{1}{2} $$ 

组合数用法与分数类似，在命令前加d和t也能达到分数字号设置同样的功能

\binom{233}{x^2}

5. 运算符

基本加减乘除等于 +-*/= 可以直接输入
特殊运算则用以下特殊命令\pm; \times; \div; \cdot; \cap; \cup; \geq; \leq; \neq; \approx; \equiv

在此之上，如果想要使用堆积符号有以下三种形式

• \stackrel{上位符号}{基位符号} 基位符号大，上位符号小
• {上位公式\atop 下位公式} 上下符号一样大
• {上位公式\choose 下位公式} 上下符号一样大；上下符号被包括在圆弧内

和、积、极限、积分等运算符用\sum, \prod, \lim, \int,这些公式在行内公式被压缩，以适应行高，可以通过\limits和\nolimits命令其是否压缩。

$ \sum_{i=1}^n i $

$ \prod_{i=1}^n i$

$\lim_{x\to0}x^2 $

$\int_{a}^{b}x^2 dx $

$\sum\nolimits_{i=1}^n i \quad\prod\nolimits_{i=1}^n i
\quad
\lim\nolimits_{x\to0}x^2 \quad\int\limits_{a}^{b}x^2 dx 
$

6. 积分及箭头

积分符号使用如下形式：\int、\iint、\iiint、\iiiint、\idotsint

$$ \int \int \quad \int \int \int \quad 
 \int \int \int \int \quad \int \dots（表示...） \int $$

$$ \iint \quad \iiint \quad \iiiint \quad \idotsint $$

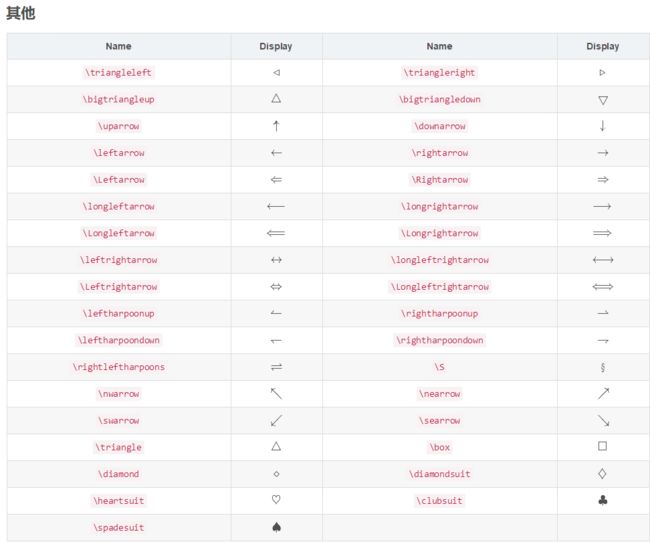
箭头的种类过于繁多，这里不就一一列举了，但是箭头符号的名字很有规律，一般命名规则为方向+箭头种类：

代码	显示
\leftarrow 或 \gets
\rightarrow 或 \to
\uparrow
\downarrow

四个基本方向上下左右不多说，斜着的箭头的方向部分为\ne \se \nw \sw，为东北、东南、西北、西南简写
示例：\nearrow

还有左右、上下两个方向的箭头：
\leftrightarrow
\updownarrow

上面的箭头只有一根线，可以通过大写第一个字母变成双线：
\Leftrightarrow
\Uparrow

在前面加上long可以把箭头变长，仅适用于左右箭头，注意双线箭头大写字母的位置：
\longleftarrow
\longleftrightarrow
\Longleftrightarrow 或 \iff

还有只有一边的箭头，名字为harpoon+up/down，表示那一边的位置，这种箭头似乎不支持上面的buff buffbuff，但拥有左右双向箭头：
\leftharpoonup
\rightleftharpoons

意图在箭头上下位置添加说明时，有以下两种方式

1.\xleftarrow和\xrightarrow可根据内容自动调整（上下都可以添加内容）

2.\overset{}{\rightarrow}则是长度固定的箭头，适合单个字符，内容在上
  \overrightarrow{}则是长度变化的箭头，适合多个字符，箭头在上
注意2中的都只适用于只在箭头上或下添加内容，改变位置将over改为under

$\xleftarrow[x+y+z]{x+y+z+1}$

$\xrightarrow[x+y+z+1]{x+y+z}$

$\overset{x+y+z}{\rightarrow}$

 $\underrightarrow{x+y+z}$

$\underset{x+y+z}{\leftarrow}$

 $\overleftarrow{x+y+z}$

7. 注音和标注

字母上方横线\overline{}, \bar{}
$ \bar{x} $ 单个字符 
$\overline{xyz}$ 多个字符

字母下方横线\underline{}
$\underline{xyz}$

\overbrace 和\underbrace 在表达式的上、下方给出一水平的大括号
$\overbrace{a\dots a}^{n个}$ 
$\underbrace{a\dots a}_{n个}$ 

向量表示有两种，单个字母用\vec{x}，多个字母用\overrightarrow 和\overleftarrow
$ \vec{x}$
$\overrightarrow{AB}$
$\overleftarrow{ABC}$

字母上方波浪线\tilde{}, \widetilde{}
$ \tilde{x}$
$ \widetilde{xyz}$

$ \dot{x}$

$ \hat{x}$ 
$ \widehat{xyz}$ 

$ \acute{x}$

$ \grave{x} $

$ \mathring{x}$

$ \ddot{x}$

$ \check{x} $

$ \breve{x}$

$ \dddot{x} $

8. 编号

插入编号：
使用\tag指令指定公式的具体编号，并使用\label指令埋下锚点。如y=x^2 \tag{1.5a}

引用编号：
在markdown中不支持编号的锚点设置 \label与\ref 的使用

9. 括号及嵌套

常用括号有以下几种

image.png

括号的大小调整

对括号的大小，手动模式可以用\big, \Big, \bigg, \Bigg等一系列命令(从小到大，默认是最小)放在上述括号前面调整大小。

$\Bigg( \bigg( \Big( \big((x) \big) \Big) \bigg) \Bigg)$
$\Bigg\{ \bigg\{ \Big\{ \big\{\{x\} \big\} \Big\} \bigg\} \Bigg\}$

自动模式下要用 \left 和 \right 命令后面跟上所需分隔符，用来创建自动匹配高度的 (圆括号)，[方括号] 和 {花括号} 等分隔符

$$ f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right) $$

$$
f\left(
   \left[ 
     \frac{
       1+\left\{x,y\right\}
     }{
       \left(
          \frac{x}{y}+\frac{y}{x}
       \right)
       \left(u+1\right)
     }+a
   \right]^{3/2}
\right)
\tag{1.2}
$$

如果你需要在不同的行显示对应括号，可以在每一行对应处使用 \left. 或 \right. 来放一个"影子"括号：

$$
\begin{aligned}
a=&\left(1+2+3+  \cdots \right. \\
& \cdots+ \left. \infty-2+\infty-1+\infty\right)
\end{aligned}
$$

而如果分隔符不在左右而在中间，为了能够格式对齐，要用\middle加分隔符表示

$P=\left(A=2\middle|\frac{A^2}{B}>4\right)$

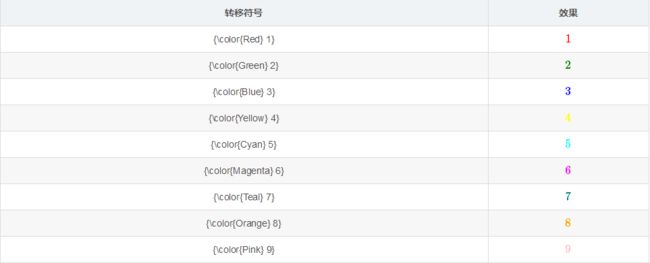
10. 颜色设置

image.png

11. 原文照排

LATEX 提供了 \verb 命令(一般用于在正文中插入较短的命令)来实现

$\verb|x^2|\quad x^2$

12. 删除线

在公式内使用 \require{cancel} 来允许 片段删除线 的显示。
声明片段删除线后，使用 \cancel{字符}、\bcancel{字符}、\xcancel{字符} 和 \cancelto{字符} 来实现各种片段删除线效果。

\require{cancel}\begin{array}{rl}
\verb|y+\cancel{x}| & y+\cancel{x}\\
\verb|\cancel{y+x}| & \cancel{y+x}\\
\verb|y+\bcancel{x}| & y+\bcancel{x}\\
\verb|y+\xcancel{x}| & y+\xcancel{x}\\
\verb|y+\cancelto{0}{x}| & y+\cancelto{0}{x}\\
\verb+\frac{1\cancel9}{\cancel95} = \frac15+& \frac{1\cancel9}{\cancel95} = \frac15 \\
\end{array}

数学公式高级规则

1. 公式环境与对齐
   在下文的公式环境中，形如 equation*中， 带*号的不将公式标号排出来, 而不带*的自动给每行式子编排标号
   latex的公式环境有很多种，这里只列举我常用的，更多请查阅latex官方说明

单行公式环境 equation
\begin{equation}
...
\end{equation}
是最一般的公式环境，表示一个公式，默认情况下之表示一个单行的公式，但是它的功能可以通过内嵌各种其他环境进行扩展，不可以使用\\与&功能。它可以内嵌的一些关于对齐的环境将在后面介绍。

$\begin{equation}
f(x)=3x^{2}+6(x-2)-1
\end{equation}$

align（多个公式）
这是最基本的对齐环境，其他多公式环境都不同程度地依赖它。它采用“&”分割各个对齐单元，使用“\\”换行。它的每行是一个公式，都会独立编号。在排版过程中，它将&分出来的列又分成组，组间特定方式排版，具体方式在flalign环境中讨论。
通常情况下在公式中可以通过\tag设置标号，\label设置引用名称，但好像的markdown不支持\label，所以编号的意义就无所谓了。

$\begin{align}
 f(x) &= (x+a)(x+b) \\
 &= x^2 + (a+b)x + ab \tag{1.1}
\end{align}$

$\begin{align}
A_{1}&=B_{1}B_{2} & A_{3} & = B_{1}\\
A_{2}&=B_{3}& A_{3}A_{4} & = B_{4}
\end{align}$

公式组环境flalign与align的功能基本相同，唯一区别是列对之间的距离为弹性宽度，以使公式组两端对齐。然而不支持。。。

gather环境
它是最简单的多行公式环境，自己不提供任何对齐。其中的各行公式按照全局方式分别对齐。
在设置了全局左对齐之后，因为不存在内部各个公式之间对排版的干扰，这种环境非常适合写数学推导或者证明。而默认情况下，是居中对齐。

\begin{gather*}
E(X)=\lambda    \qquad  D(X)=\lambda    \\
E(\bar{X})=\lambda  \\
D(\bar{X})=\frac{\lambda}{n}    \\
E(S^2)=\frac{n-1}{n}\lambda \\
\end{gather*}

与上文中公式组类似的，长公式也有两种multline和split两种环境，分别对应不对齐与对齐。

multline不支持“&”分列。其首行左对齐，末行右对齐，其余各行分别按照全局方式对齐。
split也用于排版多行公式，但它与多行公式环境multline的区别主要是以下三点：

• 用&作为分列符，但至多两列；左列右对齐，右列左对齐，形成一个列对，可使多行公式关于某个符号垂直对齐。因此用它排版的多行公式更为整齐美观。如果不用分列符&,所有公式行为一列，且全都与首行公式的右端对齐。
• 必须置于除multline环境之外的其它公式环境中。
• 自身并不生成公式序号，而是由外在公式环境提供，序号垂直居中。

示例如下：

$$\begin{multline}
x=a+b+c+{} \\
d+e+f+g
\end{multline}$$

$$\begin{split}
x=&a+b+c+{} \\
&d+e+f+g
\end{split}$$

/gathered，/aligned。以上几种方程组环境，无论每个公式多小，都会占满一行。而/gathered，/aligned环境，则只占据公式的实际宽度，整体作为一个特大的符号与其他符号一同处理。
这个结构还可以添加位置参数，以决定与其他符号的竖直对齐方式(b,t)。而且这种环境不再具有自动编号功能。

$\begin{equation}
 \left.\begin{aligned}
        B'&=-\partial \times E,\\
        E'&=\partial \times B - 4\pi j,
       \end{aligned}
 \right\}
 \qquad \text{Maxwell's equations}
\end{equation}
$

$\begin{equation}
\left.
\begin{aligned}
x+y &> 5 \\
y-y &> 11
\end{aligned}
\ \right\}\Rightarrow x^2 - y^2 > 55
\end{equation}$

cases环境常用于分段函数，上面的环境虽然支持分段函数形式的表达，但比较繁琐

$$
L(Y,f(X))=
\begin{cases}
1,\quad &Y\neq f(X)\\
0,\quad &Y=f(X)
\end{cases}
$$

阵列环境 array可以帮助我们输入一个数组或表格
通常，一个格式化后的表格比单纯的文字或排版后的文字更具有可读性。数组和表格均以 begin{array} 开头，并在其后定义列数及每一列的文本对齐属性，字母c l r 分别代表居中、左对齐及右对齐。若需要插入垂直分割线，在定义式中插入 | ，若要插入水平分割线，在下一行输入前插入 \hline 。与矩阵相似，每行元素间均须要插入 & ，每行元素以 \ 结尾，最后以 end{array} 结束数组。下面是几个示例：

$\begin{array}{c|l|c|r}
n & \text{左对齐} & \text{居中对齐} & \text{右对齐} \\
\hline
1 & 0.24 & 1 & 125 \\
\hline
2 & -1 & 189 & -8 \\
\hline
3 & -20 & 2000 & 1+10i
\end{array}$

$\left(\begin{array}{ccc|c}
 a11 & a12 & a13  & b1 \\
a21 & a22  & a23 & b2  \\ 
a31 & a32  & a33 & b3  \\
 \end{array}\right)$

$$
\left\{ 
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\ 
a_2x+b_2y+c_2z=d_2 \\ 
a_3x+b_3y+c_3z=d_3
\end{array}
\right. 
$$

2. 矩阵

• 第一种方式：使用matrix、pmatrix、bmatrix、Bmatrix、vmatrix或者Vmatrix，smallmatrix
  一个最基本的矩阵

$ \begin{matrix}
0 & 1 \\
1 & 0 
\end{matrix} $   

可以看到矩阵中用 & 分隔列，用 \\ 分隔行，在矩阵开始和结束部分\begin和\end+矩阵类型
下面给出这几种矩阵类型的图示

矩阵类型	矩阵图示
matrix
pmatrix
bmatrix
Bmatrix
vmatrix
Vmatrix
smallmatrix

在此之上，如果我们需要对矩阵起始和结束部分的括号进行变化，可以使用诸如

$\left\{\begin{matrix}
 x_1& x_2\\ 
 y_1& y_2
\end{matrix}\right.$    (此处.作为占位符表示不需要分隔符)
$\left.\begin{matrix}
x_1 & x_2\\ 
 y_1& y_2
\end{matrix}\right\}$  

第二种方式就是使用array环境，在左右端加上所需括号即可

输入带省略符号的矩阵

$$
        \begin{pmatrix}
        1 & a_1 & a_1^2 & \cdots & a_1^n \\
        1 & a_2 & a_2^2 & \cdots & a_2^n \\
        \vdots & \vdots & \vdots & \ddots & \vdots \\
        1 & a_m & a_m^2 & \cdots & a_m^n \\
        \end{pmatrix}
$$

3. 交换图表

使用一行 \require{AMScd} 语句来允许交换图表的显示。
声明交换图表后，语法与矩阵相似，在开头使用 begin{CD}，在结尾使用 end{CD}，在中间插入图表元素，每个元素之间插入 & ，并在每行结尾处使用 \ 。

$\require{AMScd}
\begin{CD}
    A @>a>> B\\
    @V b V V\# @VV c V\\
    C @>>d> D
\end{CD}$

其中，@>>> 代表右箭头、@<<< 代表左箭头、@VVV 代表下箭头、@AAA 代表上箭头、@= 代表水平双实线、@| 代表竖直双实线、@.代表没有箭头。
在 @>>> 的 >>> 之间任意插入文字即代表该箭头的注释文字。

$\begin{CD}
    A @>>> B @>{\text{very long label}}>> C \\
    @. @AAA @| \\
    D @= E @<<< F
\end{CD}$

以上内容大致上应该能把绝大多数数学公式优美的书写下来了，更多内容还需要自行查阅官方说明~~