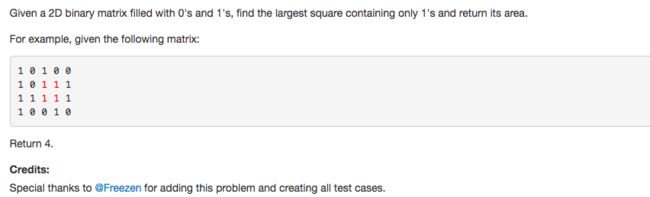
这题我写了第一行就发现无从下笔。。。这个看起来很像continous islands那道题,但是又有许多不一样。比如说他要求面积,你就需要知道长和宽。 然后还需要判断是不是一个square. 全程懵逼找不到突破口。
大概所有人都以为这是一道search题? 像number of islands, word search那种吧?
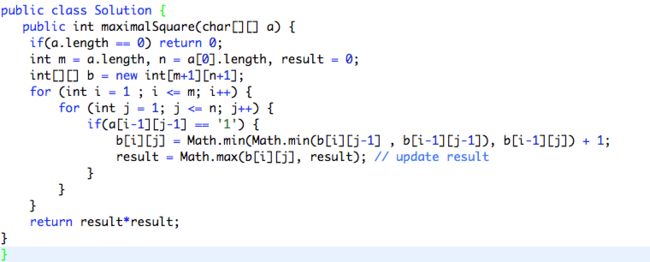
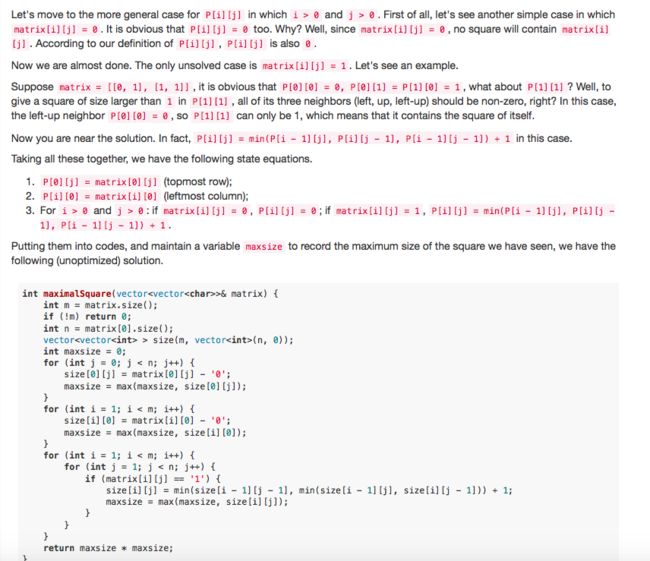
m = 整个input的row height, n = col width. result 为目标square的width
建立了一个跟input matrix差不多大的matrix b。【为了Dynamic Programming】
遍历整个input的matrix,如果发现某个位置上是"1", 那么dp[i][j]上面做一个判断,
这一步非常的tricky+ confusing。
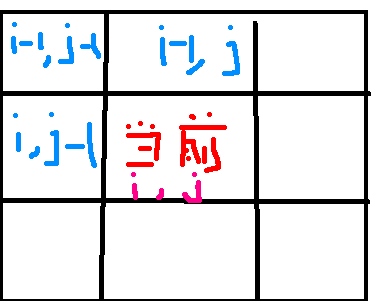
判断3个东西哪个最小。 b[i][j-1]是同一行,左边一个col的positiom. b[i-1][j-1]是上一行,左一个的position。b[i-1][j]是上一行,同一个col的位置。
为什么要判断左边,左上角,上方哪个最小呢?然后这里又哪里判断了这是不是个正方形???
经过一些时间的研究,发现这个解法简直是神级! 他验证正方向的方式是一种很隐形的验证。
只有 1 1 左,上,左上角三个位置都是1的时候,才确定当前位置是属于一个square里的
1 1
DP的当前位置i, j 会update成 min(1,1,1)--> 1+1 =2 也就是square width =2. area= 2*2 =4.
如果是 0 1
1 1 这种, 左上角是个0, 所以 当前位置会update DP array = 0 + 1=1.
square width =1, area = 1*1 =1.
1 1 1
1 1 1
1 1 1 也hold true, 当我们到右下角的时候, 上,左,左上角3个位置DP value都是2. 这样
min(2,2,2)+1 ---> 3。 所以更新square width =3. area = 3*3 =9.
update 一下result 的width. result 等于b[i][j]和 之前最大的square width哪个大。
这种题,我觉得也是属于没有见过的话必死的题。 基本上面试时候不可能看出题目的破绽来解。
Edit on 8月8日:
网上大神竟然直接把这题转换成Largest Rectangle in Histogram 来做。。太强了
这尼玛。。。原来是maximal rectangle可以那样做。。。
Edit on 2017.9.20
重新回顾这个经典题,发现比我想象的还要难,并且发现DP最优解也不是一开始就出现的。
其实蓝色绿色黄色都在绿色部分有一个Intersection。
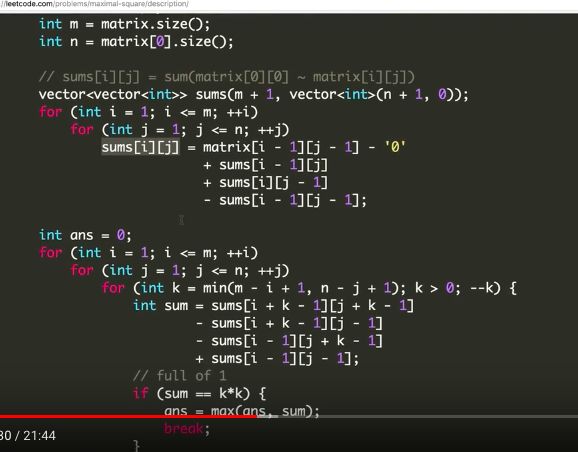
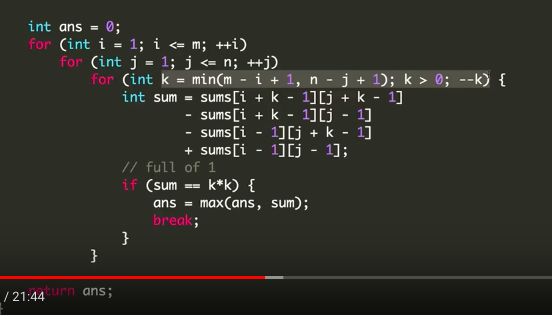
O(n^3) 第一次Loop pre-processing得到DP矩阵记录所有各种size square的Sum。可以认为是求出了所有的Square Sum。
第二次Loop求出里头最大的。注意,在第二次Loop的时候,只有Square size^2==Square Sum时候,我们才看看他是不是max square. 因为当Square size^2==Square Sum,代表正方形里全是1,是一个真的square!
这题很有战略意义,求max square sum之类的也可以用 尽管不是最优解。