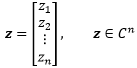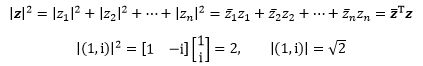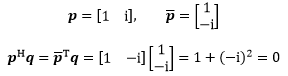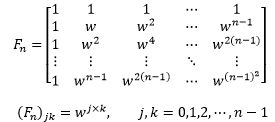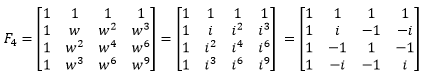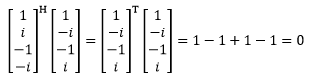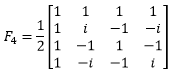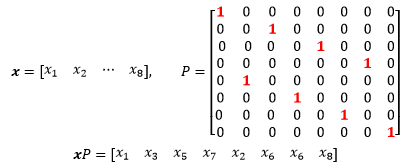原文 | https://mp.weixin.qq.com/s/YzPoPnRb-gEm_EiV9et0TA
实矩阵也可能碰到复特征值,因此无可避免地在矩阵运算中碰到复数。
矩阵当然也有可能包含复数,最重要的复矩阵是傅立叶矩阵,它用于傅立叶变换。一种特殊的傅立叶变换是快速傅立叶变换(fast Fourier transform),简称FFT,在计算机中很常用,特别是涉及到大数据时,FFT将把傅立叶变换中的n阶方正阵乘法的运算次数从n2降低到nlog2n,这是一个巨大的进步。
本文相关前置知识
复数和复平面、复平面上的旋转
傅立叶矩阵中w的由来
标准正交矩阵及其性质
复矩阵的特征值
复向量
先给出一个复向量,即向量的分量中至少有一个是复数:
虽然这个向量在表达上和普通的实向量没什么区别,但这个向量不再属于实空间Rn,而是属于复空间Cn,即n维复空间。
模长
关于复向量的第一个问题是模长怎么计算?
由于向量中有复数分量,再用过zTz的方式是无法计算出模长的,比如下面的(1, i):
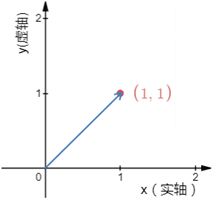
但很明显,(1, i)在复平面上的模长不是0:
我们知道一个复数的模长的平方等于这个复数与它的共轭复数的乘积,因此可以通过下面的方式计算复向量的模长:
通常用zH(H来自Hermite)表示共轭向量的转置:
![]()
点积
与模长类似,如果有两个复向量p和q,它们的点积也不能简单地定义成pTq,而是pHq:
![]()
复平面上有两个向量p(1, i)和q(1, -i),二者的点积是:
二者的点积是0,因此可以判断两个复向量互相垂直:
复矩阵
我们曾讲过,对于一个矩阵A来说,如果AT=A,那么A是对称矩阵,实际上这个结论仅对实矩阵有效,对复矩阵可不管用。
厄米特矩阵
如果一个复矩阵是对称矩阵,那么:
![]()
通常写作另一种方式:
![]()
这种对称复矩阵称为厄米特矩阵(或埃米特矩阵,Hermitian matrix),比如下面这个:
酉矩阵
上一章讲到,一个复对称矩阵的特征值仍然是实数,且可以找到互相垂直的特征向量,其对角元素都是实数。
假设有一个由n个标准正交向量组成的复矩阵Q = [q1, q2, …, qn],这里的正交意味:
这个复空间的正交矩阵Q称为酉矩阵(unitary matrix)。
傅立叶矩阵和快速傅立叶变换
傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅立叶变换用正弦波作为信号的成分。
在电子工程或计算机中,n×n矩阵的行和列都是从0开始的,到n-1结束,由于傅立叶变换经常用在计算机上,所以我们在讨论傅立叶矩阵的时候遵从这种下标规则。
傅立叶矩阵
型如Fn的复矩阵是傅立叶矩阵:
矩阵中的每个元素都不为0,是个全矩阵。w是个特殊的值:
相关链接: 傅立叶矩阵中w的由来
复数和复平面、复平面上的旋转
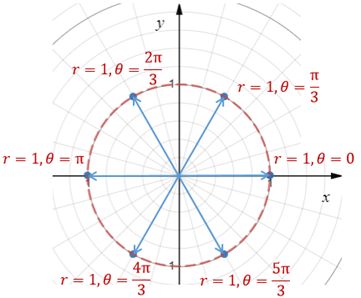
在计算w的乘方的时候,我们需要考虑用极坐标表示复平面。在极坐标下,w表示模长为1的向量从(1,0)开始,绕原点逆时针旋转了2π/n,如此一来,我们就可以知道n等于任意值时w的位置,并且也同样知道w的乘方的位置。对于w来说,wn的模长仍然等于1,只是旋转的角度有所不同。比如n=6时,w=ei2π/6= eiπ/3,w2=(eiπ/3)2= ei2π/3。
同理,n=4时,w=ei2π/4,正好落在虚轴上,w= i,w4=1。我们写出4阶傅立叶矩阵:
傅立叶矩阵可以得到一个四点(离散的)傅立叶变换,它的逆矩阵可以得到傅立叶逆变换。此外,傅立叶矩阵的列向量是正交的,所以很容易求得逆矩阵。实际上傅立叶矩阵可以分解成一系列稀疏矩阵,这些矩阵有大量的0元素,所以相应的乘法和求逆都很简单。
F4的列向量正交,这意味着任意两个列向量的点积为0,但如果你还是用过去的点积计算方法就会发现它并不是0(当然有时候会凑巧等于0),比如第2列和第4列:
前面介绍过,复向量的点积不是这么算的,正确算法应该是取共轭的转置:
F4的列向量的模长是2,为了使矩阵更完美,可以把它除以2,于是矩阵的各列就变成了标准正交向量:
对于标准正交的实矩阵来说,矩阵的逆等于矩阵的转置,傅立叶矩阵可化简为标准正交的复矩阵,具有同样的性质,F4的逆矩阵就是它共轭的转置:
![]()
由于F4的逆矩阵就是F4共轭的转置,所以F4的逆矩阵和F4具有同样的性质。
快速傅立叶变换
什么是快速傅立叶变换呢?举个例子,F6与F3之间存在着某种奇妙的联系,F8与F4,F64与F32也一样,我们可以把这种联系描述出来。
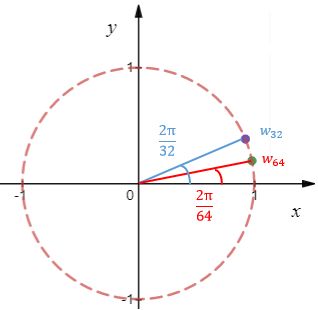
以F64与F32为例,F64是一个64阶方阵,w64 = 1,w = 1;同理对于F32来说,w32 = 1,w = 1。
w64和w32的模长相等,w64的幅角是w32的2倍:
既然如此,F64和F32也应该存在某种联系。实际上F64与由两个F32和两个零矩阵构成的方阵有关:
这种分解称为快速傅立叶变换。其中P是一个2n×2n的置换矩阵,D是由w的幂构成的对角矩阵:
P的效果是使得所乘行向量x中序号为奇数的分量x1,x3,x5……提到前面,偶数序号的分量x2,x3,x6……放到后面。例如:
可以看到,快速傅立叶变换实际上使用的是分治算法。计算64阶傅立叶变换的计算量是642,而经过一次变换后,计算量变成了2×322(2个32阶的傅立叶矩阵)再加上一些修正项,而修正项主要来自于和对角矩阵D的乘法,共32次。继续对F32进行分解……知道矩阵尺度为1。对于n阶矩阵,可将n2次计算降至(n/2) log2n。
作者:我是8位的
出处:https://mp.weixin.qq.com/s/YzPoPnRb-gEm_EiV9et0TA
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注作者公众号“我是8位的”