作者:白介素2
相关阅读:
[R语言生存分析03-Cox比例风险模型]
R语言生存分析-02-ggforest
R语言生存分析-01
ggpubr-专为学术绘图而生(二)
ggstatsplot-专为学术绘图而生(一)
生存曲线
R语言GEO数据挖掘01-数据下载及提取表达矩阵
R语言GEO数据挖掘02-解决GEO数据中的多个探针对应一个基因
R语言GEO数据挖掘03-limma分析差异基因
R语言GEO数据挖掘04-功能富集分析
如果没有时间精力学习代码,推荐了解:零代码数据挖掘课程
Cox比例风险模型
- The Cox proportional-hazards model (Cox, 1972) Cox比例风险模型是常用与医学研究中的回归模型,通常用于研究预测变量与生存时间的关系
- Kaplan-Meier curves 与 logrank test tests属于单因素分析的例子,他们研究的是单一变量与生存的关系,并且Kaplan-Meier 与log-rank检验只适用于分类变量,却并不适用于数值型变量,比如我们常见的基因表达
- Cox比例风险回归分析的优势在于可以分析分类变量与数值变量,并且将生存分析的范围由单因素拓展到多因素的分析.
Cox比例风险模型基础知识
- 在临床研究中,存在许多情况,其中几个已知量(称为协变量)可能影响患者预后。
- 例如,假设比较两组患者:具有和没有特定基因型的患者。如果其中一组也包含较老的个体,则存活率的任何差异可归因于基因型或年龄或两者。因此,在研究与任何一个因素相关的生存时,通常需要调整其他因素的影响。
- 统计模型是一种常用工具,可以同时分析几个因素的生存。另外,统计模型提供每个因素的效果大小。
- cox比例风险模型是用于对生存分析数据建模的最重要方法之一。
- 该模型的目的是同时评估几个因素对生存的影响。换句话说,它允许我们检查特定因素如何影响特定时间点发生的特定事件(例如,感染,死亡)的发生率。这个比率通常被称为危险率。 预测变量(或因子)通常在生存分析文献中称为协变量。
h(t)=h0(t)×exp(b1x1+b2x2+...+bpxp)公式可以描述为t代表生存时间,h(t)是风险函数,由协变量x1,x2,x3等决定,b1,b2,b3等代表的是协变量的系数,即该变量对生存时间影响的大小,h0(t)表示的是基线风险
exp(bi)指的是Hazard Ratio,HR,
- HR = 1: 无效应
- HR < 1: 风险减少
- HR > 1: 风险增加
实例代码演示
Sys.setlocale('LC_ALL','C')
library("survival")
library("survminer")
计算风险模型的函数 coxph()
survival::coxph(formula, data, method)
formula是带有生存对象的线性模型,生存对象用Surv(time,event)
data是带有协变量的数据框,method是方法,一般默认efron
加载实例数据集
data("lung")
head(lung)
## inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
## 1 3 306 2 74 1 1 90 100 1175 NA
## 2 3 455 2 68 1 0 90 90 1225 15
## 3 3 1010 1 56 1 0 90 90 NA 15
## 4 5 210 2 57 1 1 90 60 1150 11
## 5 1 883 2 60 1 0 100 90 NA 0
## 6 12 1022 1 74 1 1 50 80 513 0
单因素Cox回归分析
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
res.cox
## Call:
## coxph(formula = Surv(time, status) ~ sex, data = lung)
##
## coef exp(coef) se(coef) z p
## sex -0.5310 0.5880 0.1672 -3.176 0.00149
##
## Likelihood ratio test=10.63 on 1 df, p=0.001111
## n= 228, number of events= 165
生成完整的结果报告
summary(res.cox)
## Call:
## coxph(formula = Surv(time, status) ~ sex, data = lung)
##
## n= 228, number of events= 165
##
## coef exp(coef) se(coef) z Pr(>|z|)
## sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## sex 0.588 1.701 0.4237 0.816
##
## Concordance= 0.579 (se = 0.021 )
## Likelihood ratio test= 10.63 on 1 df, p=0.001
## Wald test = 10.09 on 1 df, p=0.001
## Score (logrank) test = 10.33 on 1 df, p=0.001
str(summary(res.cox))##是一个list
## List of 14
## $ call : language coxph(formula = Surv(time, status) ~ sex, data = lung)
## $ fail : NULL
## $ na.action : NULL
## $ n : int 228
## $ loglik : num [1:2] -750 -745
## $ nevent : num 165
## $ coefficients: num [1, 1:5] -0.53102 0.588 0.16718 -3.17638 0.00149
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr "sex"
## .. ..$ : chr [1:5] "coef" "exp(coef)" "se(coef)" "z" ...
## $ conf.int : num [1, 1:4] 0.588 1.701 0.424 0.816
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr "sex"
## .. ..$ : chr [1:4] "exp(coef)" "exp(-coef)" "lower .95" "upper .95"
## $ logtest : Named num [1:3] 10.6336 1 0.00111
## ..- attr(*, "names")= chr [1:3] "test" "df" "pvalue"
## $ sctest : Named num [1:3] 10.32515 1 0.00131
## ..- attr(*, "names")= chr [1:3] "test" "df" "pvalue"
## $ rsq : Named num [1:2] 0.0456 0.9986
## ..- attr(*, "names")= chr [1:2] "rsq" "maxrsq"
## $ waldtest : Named num [1:3] 10.09 1 0.00149
## ..- attr(*, "names")= chr [1:3] "test" "df" "pvalue"
## $ used.robust : logi FALSE
## $ concordance : Named num [1:2] 0.5786 0.0207
## ..- attr(*, "names")= chr [1:2] "C" "se(C)"
## - attr(*, "class")= chr "summary.coxph"
结果解释
- Statistical significance:z给出的是waldtest的统计量,它对应于每个回归系数与其标准误差的比率(z = coef/se(coef)。wald统计量评估给定变量的β(β)系数是否在统计学上显着不同于0从上面的输出,我们可以得出结论,变量性别具有高度统计上显著的系数。
- coef: regression coefficients,回归系数,coef正值表示高风险,在R中HR值是给出第二组与第一组的比值,比如这里的coef=-0.53意味着female Vs. male 95%CI: lower upper
- 整体统计学意义: 最后,输出给出了模型总体显着性的三个替代测试的p值:似然比检验,Wald检验和得分数据统计.这三种方法是渐近等价的.对于足够大的N,它们将给出类似的结果。 对于小N,它们可能有所不同。对于小样本量,似然比检验具有更好的行为,因此通常是优选的。
批量进行单因素Cox生存分析
配合lapply函数进行批量分析,写出单因素批量分析的函数
covariates <- c("age", "sex", "ph.karno", "ph.ecog", "wt.loss")
得到一个列表分别为,对每个变量构建的生存对象公式
univ_formulas <- sapply(covariates,
function(x) as.formula(paste('Surv(time, status)~', x)))
univ_formulas
## $age
## Surv(time, status) ~ age
##
##
## $sex
## Surv(time, status) ~ sex
##
##
## $ph.karno
## Surv(time, status) ~ ph.karno
##
##
## $ph.ecog
## Surv(time, status) ~ ph.ecog
##
##
## $wt.loss
## Surv(time, status) ~ wt.loss
##
巧妙的配合lapply
univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)})
univ_models
## $age
## Call:
## coxph(formula = x, data = lung)
##
## coef exp(coef) se(coef) z p
## age 0.018720 1.018897 0.009199 2.035 0.0419
##
## Likelihood ratio test=4.24 on 1 df, p=0.03946
## n= 228, number of events= 165
##
## $sex
## Call:
## coxph(formula = x, data = lung)
##
## coef exp(coef) se(coef) z p
## sex -0.5310 0.5880 0.1672 -3.176 0.00149
##
## Likelihood ratio test=10.63 on 1 df, p=0.001111
## n= 228, number of events= 165
##
## $ph.karno
## Call:
## coxph(formula = x, data = lung)
##
## coef exp(coef) se(coef) z p
## ph.karno -0.016448 0.983686 0.005854 -2.81 0.00496
##
## Likelihood ratio test=7.56 on 1 df, p=0.005966
## n= 227, number of events= 164
## (1 observation deleted due to missingness)
##
## $ph.ecog
## Call:
## coxph(formula = x, data = lung)
##
## coef exp(coef) se(coef) z p
## ph.ecog 0.4759 1.6095 0.1134 4.198 2.69e-05
##
## Likelihood ratio test=17.57 on 1 df, p=2.773e-05
## n= 227, number of events= 164
## (1 observation deleted due to missingness)
##
## $wt.loss
## Call:
## coxph(formula = x, data = lung)
##
## coef exp(coef) se(coef) z p
## wt.loss 0.001319 1.001320 0.006079 0.217 0.828
##
## Likelihood ratio test=0.05 on 1 df, p=0.8289
## n= 214, number of events= 152
## (14 observations deleted due to missingness)
提取出分析结果
- 创建提取批量分析结果的函数
- 提取分析结果,转换为数据框输出 注意是列表元素的提取,
- exp(coef)指的是HR,beta值是系数
univ_results <- lapply(univ_models,
function(x){
x <- summary(x)
p.value<-signif(x$wald["pvalue"], digits=2)
wald.test<-signif(x$wald["test"], digits=2)
beta<-signif(x$coef[1], digits=2);#coeficient beta
HR <-signif(x$coef[2], digits=2);#exp(beta)
HR.confint.lower <- signif(x$conf.int[,"lower .95"],2)
HR.confint.upper <- signif(x$conf.int[,"upper .95"],2)
HR <- paste0(HR, " (",
HR.confint.lower, "-", HR.confint.upper, ")")
res<-c(beta, HR, wald.test, p.value)
names(res)<-c("beta", "HR (95% CI for HR)", "wald.test", "p.value")
return(res)
#return(exp(cbind(coef(x),confint(x))))
})
class(univ_results)
## [1] "list"
str(univ_results)
## List of 5
## $ age : Named chr [1:4] "0.019" "1 (1-1)" "4.1" "0.042"
## ..- attr(*, "names")= chr [1:4] "beta" "HR (95% CI for HR)" "wald.test" "p.value"
## $ sex : Named chr [1:4] "-0.53" "0.59 (0.42-0.82)" "10" "0.0015"
## ..- attr(*, "names")= chr [1:4] "beta" "HR (95% CI for HR)" "wald.test" "p.value"
## $ ph.karno: Named chr [1:4] "-0.016" "0.98 (0.97-1)" "7.9" "0.005"
## ..- attr(*, "names")= chr [1:4] "beta" "HR (95% CI for HR)" "wald.test" "p.value"
## $ ph.ecog : Named chr [1:4] "0.48" "1.6 (1.3-2)" "18" "2.7e-05"
## ..- attr(*, "names")= chr [1:4] "beta" "HR (95% CI for HR)" "wald.test" "p.value"
## $ wt.loss : Named chr [1:4] "0.0013" "1 (0.99-1)" "0.05" "0.83"
## ..- attr(*, "names")= chr [1:4] "beta" "HR (95% CI for HR)" "wald.test" "p.value"
res <- t(as.data.frame(univ_results, check.names = FALSE))
as.data.frame(res)
## beta HR (95% CI for HR) wald.test p.value
## age 0.019 1 (1-1) 4.1 0.042
## sex -0.53 0.59 (0.42-0.82) 10 0.0015
## ph.karno -0.016 0.98 (0.97-1) 7.9 0.005
## ph.ecog 0.48 1.6 (1.3-2) 18 2.7e-05
## wt.loss 0.0013 1 (0.99-1) 0.05 0.83
通过单因素分析我们得出age,sex,ph.ecog,ph.karno具有统计学意义,由于wt.loss变量无统计学意义,我们在接下来的多因素Cox回归分析中跳过改变量,将四个变量纳入进入分析. 多因素分析回答的是,这些因素如何共同影响生存时间
多因素Cox回归
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog + ph.karno, data = lung)
res.cox
## Call:
## coxph(formula = Surv(time, status) ~ age + sex + ph.ecog + ph.karno,
## data = lung)
##
## coef exp(coef) se(coef) z p
## age 0.012868 1.012951 0.009404 1.368 0.171226
## sex -0.572802 0.563943 0.169222 -3.385 0.000712
## ph.ecog 0.633077 1.883397 0.176034 3.596 0.000323
## ph.karno 0.012558 1.012637 0.009514 1.320 0.186842
##
## Likelihood ratio test=31.27 on 4 df, p=2.695e-06
## n= 226, number of events= 163
## (2 observations deleted due to missingness)
summary(res.cox)
## Call:
## coxph(formula = Surv(time, status) ~ age + sex + ph.ecog + ph.karno,
## data = lung)
##
## n= 226, number of events= 163
## (2 observations deleted due to missingness)
##
## coef exp(coef) se(coef) z Pr(>|z|)
## age 0.012868 1.012951 0.009404 1.368 0.171226
## sex -0.572802 0.563943 0.169222 -3.385 0.000712 ***
## ph.ecog 0.633077 1.883397 0.176034 3.596 0.000323 ***
## ph.karno 0.012558 1.012637 0.009514 1.320 0.186842
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## age 1.0130 0.9872 0.9945 1.0318
## sex 0.5639 1.7732 0.4048 0.7857
## ph.ecog 1.8834 0.5310 1.3338 2.6594
## ph.karno 1.0126 0.9875 0.9939 1.0317
##
## Concordance= 0.632 (se = 0.025 )
## Likelihood ratio test= 31.27 on 4 df, p=3e-06
## Wald test = 30.61 on 4 df, p=4e-06
## Score (logrank) test = 31.06 on 4 df, p=3e-06
可视化生存时间分布
survfit() 用于评估生存比例,默认各协变量的平均值 可视化基线生存时间分布
survfit(res.cox)
## Call: survfit(formula = res.cox)
##
## n events median 0.95LCL 0.95UCL
## 226 163 329 286 364
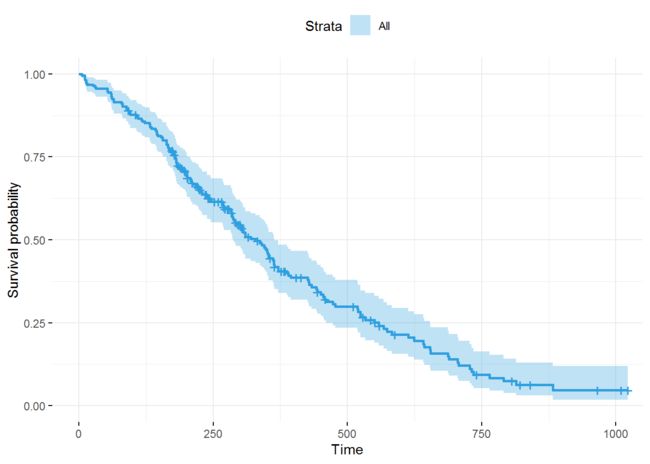
ggsurvplot(survfit(res.cox),data = lung, color = "#2E9FDF",
ggtheme = theme_minimal())
## Warning: Now, to change color palette, use the argument palette= '#2E9FDF'
## instead of color = '#2E9FDF'
展示感兴趣的变量如何影响生存分布
原文中的教程较复杂,且并可行,这里我只用自己的简单方法
构建surfut生存对象,与感兴趣的变量建立公式
fit<- survfit(Surv(time, status) ~ sex, data = lung)
fit
##
##Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
## n events median 0.95LCL 0.95UCL
##sex=1 138 112 270 212 310
##sex=2 90 53 426 348 550
##
绘制简单的曲线非常简单::ggsurvplot函数
ggsurvplot(fit, data = lung)
深度定制,这个前几期的内容似乎已经涉及了,就不再重复了
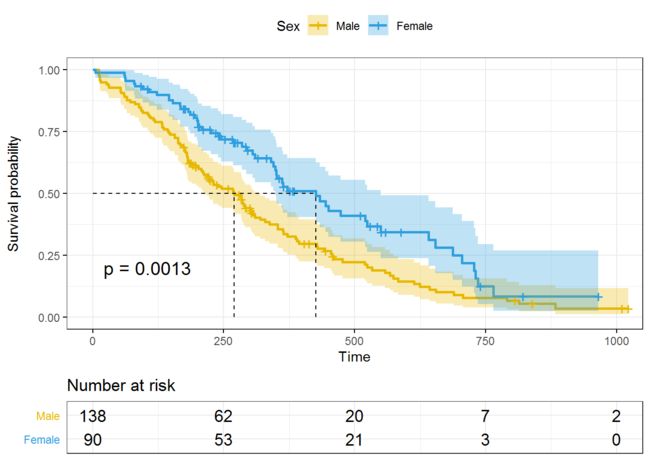
ggsurvplot(fit, data = lung,
surv.median.line = "hv", # Add medians survival
# Change legends: title & labels
legend.title = "Sex",
legend.labs = c("Male", "Female"),
# Add p-value and tervals
pval = TRUE,
conf.int = TRUE,
# Add risk table
risk.table = TRUE,
tables.height = 0.2,
tables.theme = theme_cleantable(),
# Color palettes. Use custom color: c("#E7B800", "#2E9FDF"),
# or brewer color (e.g.: "Dark2"), or ggsci color (e.g.: "jco")
palette = c("#E7B800", "#2E9FDF"),
ggtheme = theme_bw() # Change ggplot2 theme
)
本期内容就到这里,我是白介素2,下期再见
参考资料链接