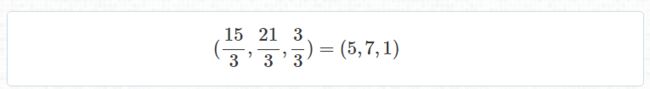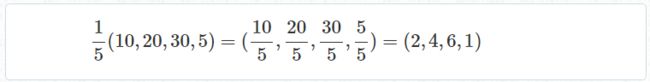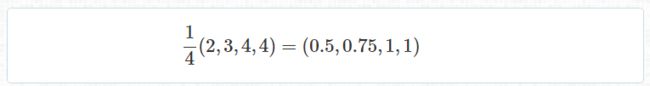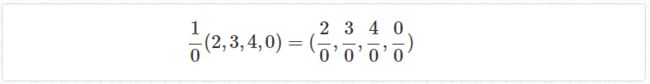齐次坐标在计算机图形中的应用

原文: CC老师
著作所属权归该作者所有,任何形式转载请联系作者并注明原文出处.

提示: 齐次坐标是在学习OpenGL ES 初期百思不得其解的地方. 希望这篇文章能够给你帮助.此文将苹果由CoreAnimation 透视投影为引子.为什么需要用4*4矩阵来描述坐标变换?

核心动画苹果文档-透视投影效果的设置

The sublayerTransform property defines additional transformations that apply only to the sublayers and is used most commonly to add a perspective visual effect to the contents of a scene.

Transforms work by multiplying coordinate values through a matrix of numbers to get new coordinates that represent the transformed versions of the original points. Because Core Animation values can be specified in three dimensions, each coordinate point has four values that must be multiplied through a four-by-four matrix, as shown in Figure 1-7. In Core Animation, the transform in the figure is represented by the CATransform3D type. Fortunately, you do not have to modify the fields of this structure directly to perform standard transformations. Core Animation provides a comprehensive set of functions for creating scale, translation, and rotation matrices and for doing matrix comparisons. In addition to manipulating transforms using functions, Core Animation extends key-value coding support to allow you to modify a transform using key paths. For a list of key paths you can modify, see CATransform3D Key Paths.

SublayerTransform属性定义了仅应用于子层的其他转换，并且最常用于向场景内容添加透视视觉效果。
转换的工作原理是将坐标值乘以一个数字矩阵，得到表示原始点转换版本的新坐标。因为核心动画值可以在三维中指定，所以每个坐标点有四个值，必须通过一个四乘四的矩阵相乘，如图1-7所示。在核心动画中，图形中的变换由CatTransform3D类型表示。幸运的是，您不必直接修改这个结构的字段来执行标准转换。核心动画为创建比例、平移和旋转矩阵以及进行矩阵比较提供了一套全面的功能。除了使用函数操纵变换之外，核心动画还扩展了关键值编码支持，允许您使用关键路径修改变换。有关可以修改的关键路径列表，请参见CatTransform3D关键路径。

透视投影

• 苹果文档关于单元矩阵,平移,缩放,围绕x,y,z轴旋转的矩阵

  
  
  

  矩阵变化

注意观察,你会发现为什么透视投影中3D场景,x,y,z需要W分量了? 接下来我们带着这疑惑看看苹果官方文档遗留下的问题进行探讨.

透视投影:

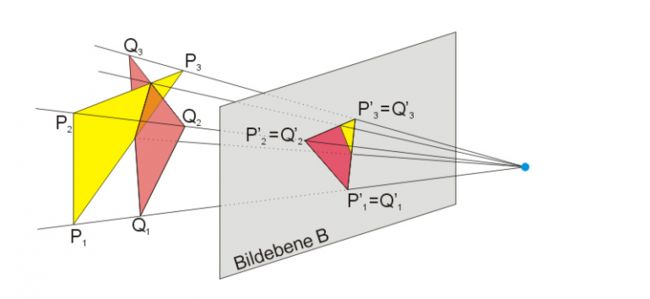
透视投影

为什么要将3D的笛卡尔坐标转换成四维齐次坐标,这样有2个主要好处:

1. 进一步完成透彻变换
2. 这样可以使用线性变换来实现模型的平移.

如果使用四维坐标系统,就可以通过矩阵乘法完成所有的旋转,平移,缩放和投影的变换操作.

什么是齐次坐标?

三维数据可以通过三维向量与3*3矩阵的乘法操作,来完成缩放和旋转的线性变换.

在大多数3D工作中，我们参照的依据是几何学中的三维空间（X, Y, Z）。
但在某些情况下，参照投影几何更适用，除了 X, Y, Z 分量外，增加一个 W 分量，这个四维空间叫做“投影空间”，在四维空间中的坐标叫“齐次坐标”。为了达到3D软件的目的，“投影的” 和 “齐次的” 可以理解为 "4D"。

注意: 四元数和齐次坐标非常类似,都是四维向量.通常也是通过(x,y,z,w)来表示,但是四元坐标和齐次坐标是不同的概念,并且适用领域也不一样. 简单说,四元数与齐次坐标没有任何关系.

• 齐次坐标是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换.
• 四元数本质上是一种高阶复数，是一个四维空间，相对于复数的二维空间。

齐次坐标在2D场景中应用

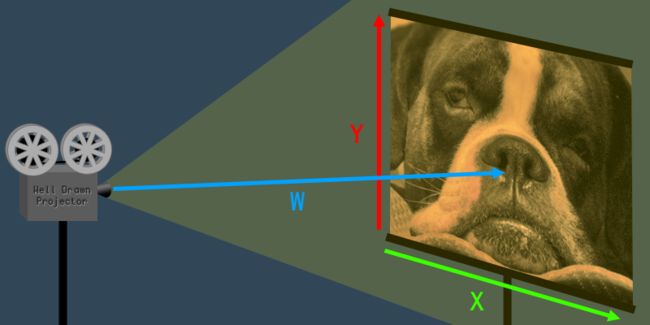
想象投影仪在一个屏幕上投影一张2D的图片,这时我们就能非常快速的理解X,Y分量的意义所在.

图1

看到这张图,我们就可以感受到投影仪与屏幕之间的距离,而这个距离就是w分量.

图2

w分量就是投影仪与屏幕的距离在开发者角度就是观察者与屏幕直接的距离.

图3

那么w分量有什么作用了?
首先我们来到这样的场景中,如果我们移动投影仪的位置,就是调整观察者的位置.来增加或减少w分量,那么投影出的2D图片会发生什么变换? 是不是如果投影仪靠近屏幕,2D图片缩小; 如果投影仪远离屏幕,2D图片就会放大; 此时通过调整观察者的位置,来实现放大与缩小的目的.W分量,会影响投影出来的图片大小;

齐次坐标在3D场景的应用

在 3D 场景下的 W 分量和 2D 场景是一样的.都是当 w 增大,坐标被拉伸; W 缩小,则坐标被压缩. W 对于 3D 坐标可以实现缩放变换.

通常,我们在图形开发中,都会建议无论什么时候将3D坐标转换为4D坐标时,让 w = 1; 那么为什么会给出这样的建议了? 因为当缩放坐标为1时,坐标不会放大或者缩小.保持原有的大小;所以当w = 1,不会影响X,Y,Z分量的值;

所以,在3D开发过程中,我们会认为坐标中w = 1 是正确的. 因为如果渲染使用W>1的坐标,则你的每个3D图形都会放大,反之,W<1的坐标中,3D物体会变小.如果渲染时,W = 0,则你的程序会崩溃,为什么? 因为计算透视除法时,除数为0; 如果 W < 0, 则渲染的图形会上下水平翻转.

但是在数学的角度, w = 1 不做强制要求. 使用齐次坐标时,w = 1 的目的仅仅是为了用于计算计算机图形学中的投影转换.

所以,你可以看到苹果文档中,关于旋转,平移,缩放等的w = 1;

矩阵变化

数学原理

图3

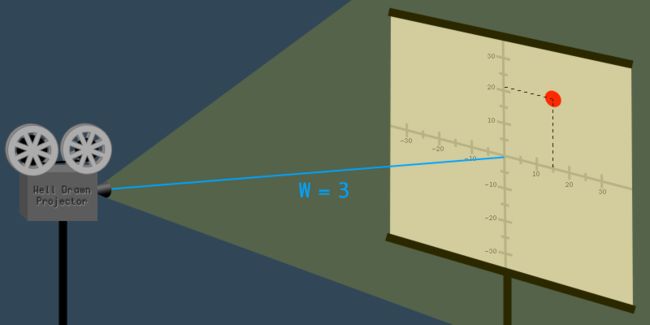
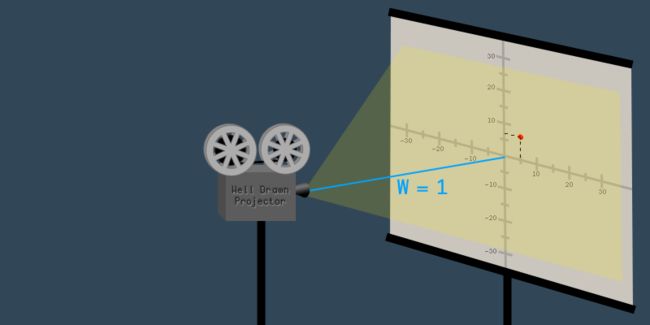
假设,在屏幕3米处设置一个投影仪,投影出一个点(15,21)在2D图像中,相应的投影坐标中的向量为(X,Y,W) = (15,21,3);

如果此时,你推动投影仪靠近屏幕,直到投影仪与屏幕之间的距离为1米;那么越靠近屏幕投影,投影的图像越小. 投影仪靠近了3倍,因此图像则缩小了3倍; 如果我们将x,y,w分量都除以3,则得到一个新的向量 w = 1;

图4

图5

此时投影出来的点在坐标中的位置改变成(5,7,1);

这就是系统如果将坐标从不规范的齐次坐标转换成一个规范齐次坐标的方法:所有分量除以w,2D和3D场景下同样适用.通过向量乘以W的倒数,来实现向量的所有分量除以w.

例如,如下3D场景下的计算

图5

• 代码实现:

//齐次坐标
vec4 vertex1(10,20,30,5);
//将坐标规范成w = 1
vec4 vertex2 = (1.0/vertex1.w) * vertex1;

齐次坐标在计算机图形学的应用

齐次坐标实现3D坐标中的转换矩阵

三维数据可以通过三维向量与 3*3 矩阵的乘法操作,来完成缩放和旋转的线性变换. 但是对于三维笛卡尔坐标的平移操作是无法通过与 3*3 矩阵的乘法操作来完成. 我们还需要一个额外的向量,将(0,0,0)移动到另外一个位置,这一步叫做仿射变换(affine transformation),它不属于线性变换. 线性变换的规则,就是它总是将(0,0,0)映射到(0,0,0).因为加入了这个额外的运算过程,我们将无法在利用线性变换的各种优势. 例如将多个变换过程合成一次变换.

所以我们找到了一个方法,就是通过线性变换来表达平移过程,就是将数据置于四维坐标空间中,仿射变换就回归到一种简单的线性变换. 也就是我们可以直接使用4*4矩阵的乘法来完成模型的移动操作.

透视投影

齐次坐标在处理矩阵变化是,第四维的W分量通常不会发生变换. 从3D转化到4D,只需要将w = 1,并且经过变换矩阵处理后,W 分量的值任然为1. 这意味着我们可以忽略W分量即可转换回3D坐标. 但是需要注意的投影矩阵则会影响W 分量

齐次坐标实现透视投影

在3D世界,物体距离相机越远看起来就越小,这个现象叫做透视. 比如下图,在镜头中,如果猫距离相机足够近,远处的大山看起来比猫小.

图6

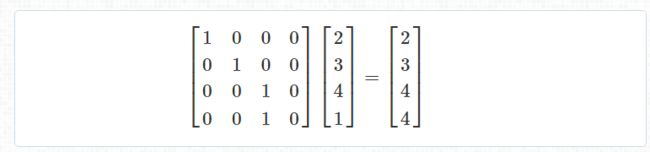
下面看一个透视例子，通过投影矩阵变换到齐次坐标。

图7

注意投影矩阵是怎样用 Z 分量改变 W 分量的。
经过投影矩阵透视变换后，每一个向量即经过了“透视除法”。透视除法只是将齐次坐标中的 W 分量转换为1的专用名词

继续上面的例子，透视除法这步如下：

图8

完成透视除法后，W分量就没用了，我们就得到了一个完全符合3D透视投影规则的3D坐标。

注意: 在OpenGL固定管线中通常使用gluPerspective 或 gluFrustum 方法。在 OpenGL 中，在顶点 shader 作用了每一个顶点后，自动进行透视除法。这就是顶点 shader 中 main 方法输出的 gl_position 变量，是4维向量，而不是3维向量。

齐次坐标影响光照平行光

齐次坐标中的一个属性，是允许有一个无限远的点（或无限长的向量），在3D坐标中这个是不允许的。当 W=0 时，这点表示无限远的一个点。如果你尝试将一个 W=0 的齐次坐标转换为一个普通的 W=1的齐次坐标，这会导致4次除0操作.此时代码会发生崩溃;

图9

这意味着，不能将 W=0 的齐次坐标转换到 3D 坐标。
那么这样的一个属性有什么用处了?

平行光可以认为是一个无限远处的点光源。当一个点光源在无限远的位置，光线就会变成平行的，并且所有光线都在同一方向，这就是平行光的基本定义。例如太阳光.

所以在传统的3D图形中，平行光可以通过改变点光源位置向量中的 W 分量来表示，当 W= 1时，是一个点光源；当 W= 0 时，是一个平行光。

例如我们在实现光照shader ,可以需要做如下判断

if (lightPosition.w == 0.0) {    
  //directional light code here
} else {
  //point light code here
}

总结:

齐次坐标有一个额外的维度叫 W 分量，用来缩放X, Y, Z三个分量的值。平移和透视投影的矩阵变换只能在齐次坐标中使用，所以在3D计算机图形学中，当 W=1时，X, Y, Z 分量被称为“正确的”。任何齐次坐标，只要 W 不为0，都可以通过将每一个分量除以 W 来转换到 W=1的向量。当 W=0 时，这个坐标表示无穷远的一个点（或者表示无限长的一个向量），通常用于表示平行光的方向。

文章参考于

Explaining Homogeneous Coordinates & Projective Geometry