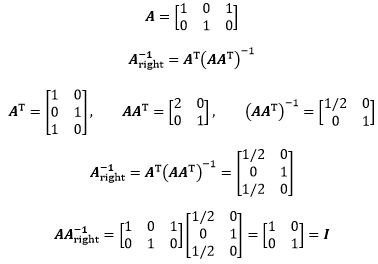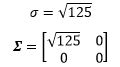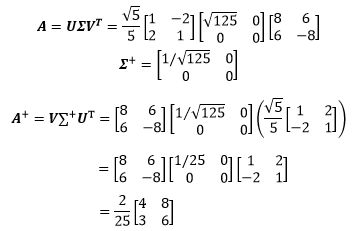线性代数笔记34——左右逆和伪逆

　　原文 | https://mp.weixin.qq.com/s/PRQQvSfmipxPBeF80aEQ1A

　　一个矩阵有逆矩阵的前提是该矩阵是一个满秩的方阵。然而很多时候遇到的都是长方矩阵，长方矩阵是否有类似的逆矩阵呢？

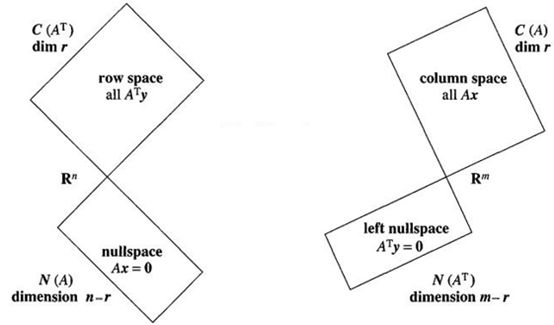
　　先把4个基本子空间的图贴上，A是m×n的矩阵，其中r是矩阵的秩：

两侧逆（2-sided inverse）

　　我们通常说的逆矩阵都是针对满秩方阵而言，此时AA^-1 = I = A^-1A，A左乘或右乘A^-1的结果都是单位矩阵，所以将这种逆矩阵称为两侧逆。

左逆（Left inverse）

　　如果A是一个m×n的列满秩矩阵，意味着A的各列线性无关，A的秩和列数相等，r = n，但A可能存在更多的行，m ≥ n，此时A的零空间只有零向量，并且Ax = b有唯一解（m = n时）或无解（m > n时）。

　　对于列满秩矩阵来说，对称矩阵A^TA是一个n×n的满秩方阵，因此A^TA可逆，此时：

　　

　　我们称A^-1_left为A的左逆，是一个n×m的矩阵，左逆也是讨论最小二乘问题的核心。

右逆（Right inverse）

　　如果A是一个m×n的行满秩矩阵，意味着A的各行线性无关，A的秩和行数相等，r = m，但A可能存在更多的列，m ≤ n。A的左零空间只有零向量，A的零空间是n - r维，因此有n – r个自由变量，当n > m时，Ax = b有无数解。

　　对于行满秩矩阵来说，对称矩阵AA^T是一个m×m的满秩方阵，因此AA^T可逆，此时：

　　通常来说，右乘左逆得不到单位矩阵，仅在m = n时才有AA^-1_left = I。对于列满秩的m×n矩阵来说，AA^-1_left = A(A^TA)^-1A^T = P，P是A的列空间的投影矩阵。同理，左乘右逆也得不到单位矩阵，A^-1_rightA是A的行空间的投影矩阵。

　　

示例 找出A的右逆：

　　Numpy的pinv函数可以求得右逆：

1 import numpy as np
2
3 A = np.mat('1 0 1; 0 1 0')
4 print(np.linalg.pinv(A))

　　

伪逆（Pseudoinverse）

　　逆矩阵可看作矩阵的逆操作，向量x在A的作用下变成了了Ax，Ax通过A^-1又得到x：

　　方阵A是否可逆和是否存在零空间有关，可逆矩阵的零空间和左零空间都只有零向量。零空间的向量是满足Ax = 0的所有x，假设A存在零空间，那么对于零空间的非零向量来说：

　　此时A的各列的线性组合是0，这意味着A的列是线性相关的，A一定不是满秩的，A是奇异矩阵，A不可逆。

　　列满秩矩阵的零空间只有零向量，有左逆矩阵；行满秩矩阵的左零空间只有零向量，有右逆矩阵。但是对于不满秩的矩阵Am×n（r < n, r < m）来说，两个零空间都存在，此时它无法得到左逆或右逆。

　　

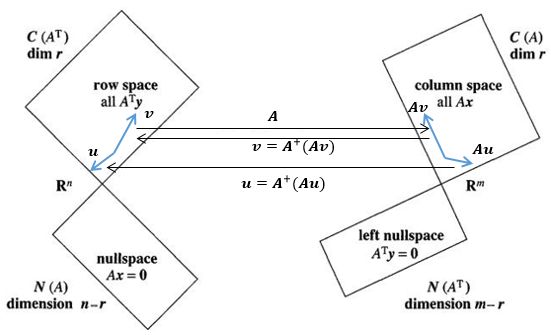
　　假设Am×n是不满秩的矩阵，其行空间和列空间的维数相等。如果此时行空间的一个向量x，经过A的变换，变为列空间的向量Ax，并且x和Ax是一一对应的（如果行空间的两个向量u ≠ v，则Au ≠ Av），那么在把逆操作限制在行空间和列空间上时，A是可以进行逆操作的，A在这两个空间上的逆矩阵称为伪逆，记作A⁺：

　　这里的关键是x和Ax是一一对应的，如果行空间的两个向量u ≠ v，则Au ≠ Av，只有这样，逆操作才成立。为什么会有一一对应？

　　u和v是行空间的两个不同的向量，经过A的转换将变成列空间的另外两个向量Au和Av。我们假设Au = Av，这相当于Au – Av = 0，即A(u – v) = 0，这意味着u – v属于零空间。但u和v是行空间的两个向量，它们的线性组合也属于行空间，与结论矛盾，因此假设不成立，Au ≠ Av。行空间和列空间的向量是一一对应的。

　　统计学家非常需要伪逆矩阵，因为他们经常使用最小二乘求解线性回归问题。统计学家经常做一些试验，并用矩阵A记录这些试验结果（每个结果有多个属性值），如果试验存在大量重复的结果，那么A将可能不是列满秩的，A^TA不可逆，无法用过去的方法解决最小二乘。此时伪逆就有了用武之地。怎样找出伪逆呢？

找出伪逆

　　A_m×n是一个不满秩矩阵，行数和列数都大于秩，m > r, n > r，找出A⁺的一个方法是利用奇异值分解。A的奇异值分解是：

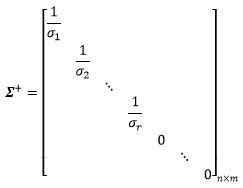
　　∑是一由奇异值构成的对角矩阵：

　　∑和A的尺寸一致，也是m×n矩阵，它的秩是r，显然也是一个不可逆矩阵，并且∑^T∑和∑∑^T都不可逆，也就是说∑也不存在左逆或右逆，只有伪逆：

　　∑⁺是一个n×m矩阵，它的秩仍然是r。伪逆是最接近逆的：

　　U和V^T都是正交矩阵，其逆矩阵等于转置，(V^T)^-1=V, U^-1 = U^T，A的伪逆为：

　　值得注意的是，AA⁺得到的并不是像∑∑⁺这样对角线上只有1和0的矩阵，而是A的行空间的投影矩阵。

伪逆的性质

　　伪逆满足4个性质：

综合示例

　　,A是否可逆？是否有左逆、右逆或伪逆？

　　

　　A的行列式是0，A是一个奇异矩阵，故A没有逆矩阵。

　　A既不是行满秩也不是列满秩，故A没有左逆或右逆，只有伪逆。

　　用奇异值分解求解A的伪逆，先对A进行奇异值分解A=UΣV_­^T。

　　先求得AA^T的特征值：

　　只有一个正的特征值125，对应的奇异值和奇异值矩阵是：

　　接下来根据根据特征方程求得AA_­^T的特征向量：

　　U是标准化后的特征向量矩阵：

　　

　　用同样的方法求得A^TA的特征值和特征向量，进而求得V。

---

　　出处：微信公众号 "我是8位的"

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注作者公众号“我是8位的”