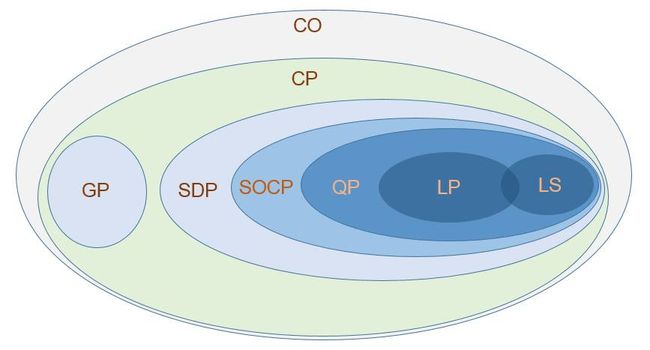
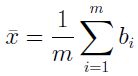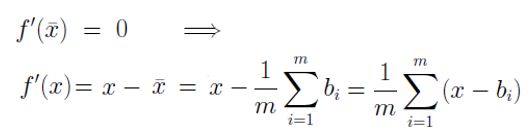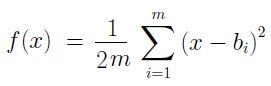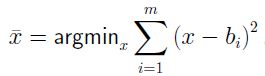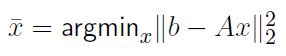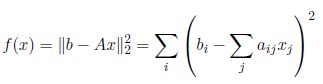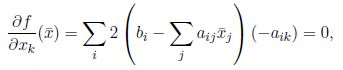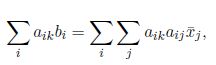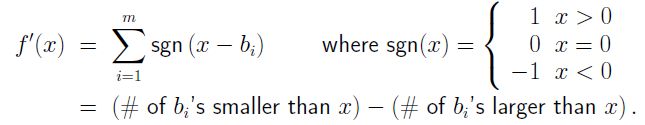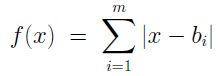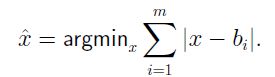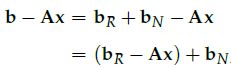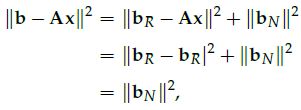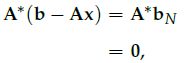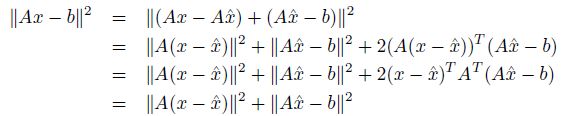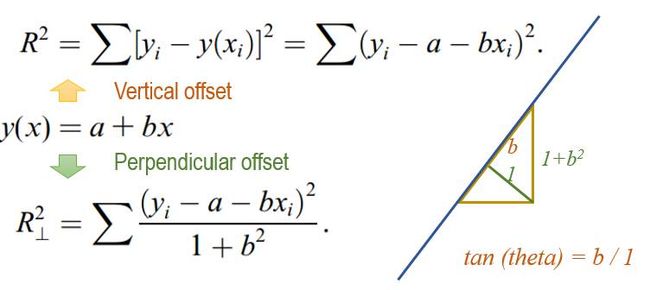一般来说凸优化(Convex Optimization, CO)中最一般的是锥规划 (Cone Programming, CP)问题, 最简单的是最小二乘(Least Square, LS)问题。
在介绍这些问题之前, 有一个前提概念,就是矩阵的四个子空间, 参考“矩有四子”。
引子
你知道Johann Bartels是谁么? 不知道吧?他是一个数学教授。 有一天, 他的邻居生了个第三个男孩, 这个男孩长得很可爱, 有一次在数学课上, 很快算出了1+2+3+...+100的那位, 对的,这就是高斯(Gauss),有一天这个孩子在门口看书, Bartels觉得特别可爱,就走过去闲聊了几句, 看他看小学数学书, 就考了下下, 发现这个男孩看书思考的特别深入。 然后, 就给他闭门开数学小灶, 并且在他14岁的时候, 带着他去见了当地的一个公爵, 说服他出一大笔钱让这个男孩深造。 在这个男孩大学学完了,牛顿(Newton), 欧拉(Euler)和拉格朗日(Lagrange)的工作后, 就一发不可收拾的成为了那个神一样的高斯。 学成完成后,这个公爵依然继续提供高薪高楼供那个男孩继续研究。 你看, 有一个数学家的邻居是多么重要呀, 现在知道学区房为啥在哪个国家都那么贵了吧?
Johann Bartels
从高斯说起
生活离不开高斯(Gauss), 好多人都不知道高斯的名字,Carl。 大部分人知道马克思(Marx)也叫类似的名字,Karl。 一个你天天用, 却感受不到, 你一个你天天感受, 却用不到。 我最喜欢这幅高斯的画像了, 像似无数的点突然间聚出一个神一样的高斯。
对的, 高斯一不小心发明了最小二乘法(Lease Square, LS), 后来根据最小二乘法和均值最优, 高斯推导出了高斯分布(Normal Distribution), 然后又根据高斯分布说明最小二乘法的价值,自圆其说。
LS, 最小二乘法的由来
还是从高斯发明最小二乘法说起, 高斯发现,均值一致广泛的天文学家们用来进行数据处理, 那么就是说均值是对一组数据最好的估算。 高斯试图理解为什么会这样, 对的, 这就是那个小男孩特别厉害的地方, 必须懂为什么,才肯放弃。 高斯做了如下推导:假如有一组数据b1, b2, .., bi, .., bm的数据,均值是最优的。
那么, 存在一个函数,在均值(Mean)点的导数为零。利用最简单的线性假设进行推理:
然后可以推导出目标函数的公式:
再反过来进行设定, 优化目标,就合情合理了, 这就是误差为什么是平方项的简单由来:
有了这个误差的目标公式, 高斯进一步推广到参数求解中:
通过类似的方法可以进行推导, 求导为零。
然后进行分解合并同类项:
利用矩阵表示:
这就是最小二乘法了, 最优解等于系数矩阵的伪逆和b的乘积。
这就是高斯对平均值深入的想了一下的结论, 然后他再深入想了一下,就是高斯分布了。 因为和这里的主题不太相关,大家可以参考Rick Jin的“正态分布的前世今生”, 或者“66天写的逻辑回归”。
有人说了, 如果当初大家用的最优值不是均值, 是不是就不一样了, 对的。 当最优值选择的是中值(Median):
利用subgradient的思想,就可以得到目标函数的公式。
直接写成如下公式:
LS, 最小二乘法的 几何意义
在讨论几何意义之前需要理解一下线性代数子空间的含义, 参考“矩有四子”。
前面给定了最小二乘法是怎么推导出来的, 也知道了均值的意义。 我们来看最小二乘法直观上的意义。
二维平面
从不可以求解的角度,因为原来的公式不可以求解, 那么希望找到其中可以求解的部分划分出来。 这样就导致有个偏差e。
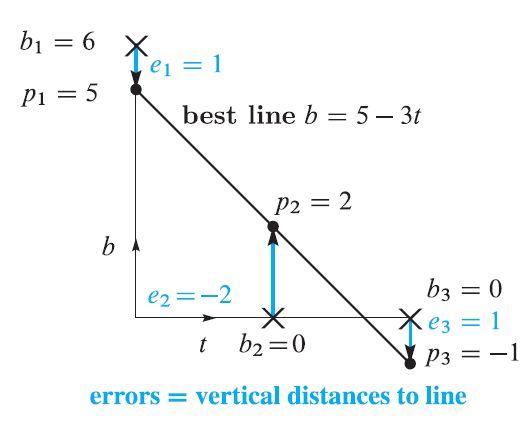
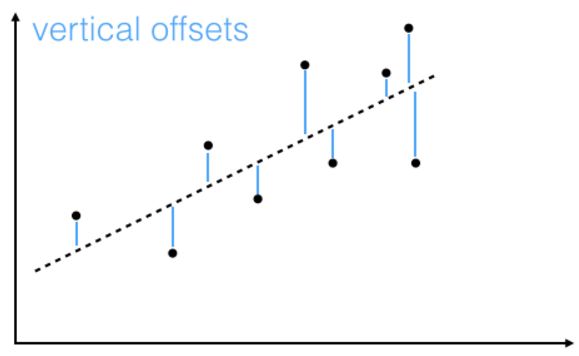
因此要求这个偏差最小。 如果在二维空间里面看, 就是找一个直线, 使得线上点在垂直方向到b的距离的平方和最小。这个垂直距离叫Vertical Offset。
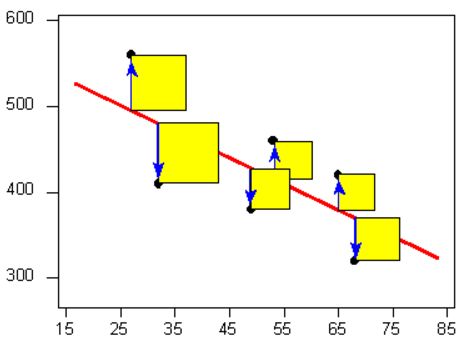
如果把平方利用面积表示, 那么就是画出一个个正方形, 要求全部正方形的面积最小的直线(黄色区域)。
高维矩阵
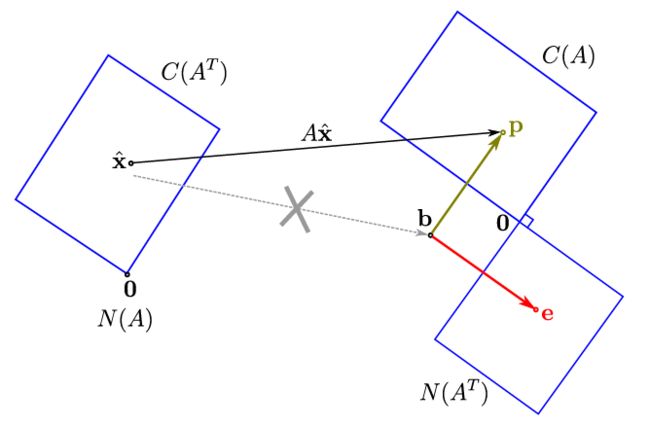
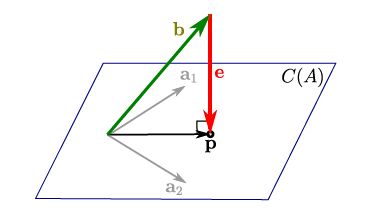
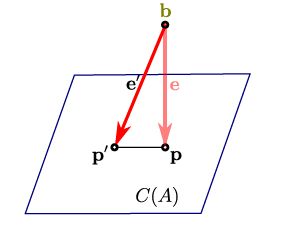
如果扩展到高维空间, 因为 Ax = b 不可解, 因此我们将 b 投影到矩阵A的两个垂直空间:列空间 Col(A) 和 左零空间Null ( A^T )上, 这样可以得到p向量和e向量。 然后这个p向量点在行空间Row(A)里面的点就是要找的最优解。
我们再来看细节,先看为什么b要投影?因为Col(A)是Ax对应所有可能空间, 但是b不属于Col(A), 所以Ax=b无解
为什么要投影到垂直空间? 因为这样得到偏差 e 是最小的, 根据列空间 Col(A) 和 左零空间Null ( A^T )垂直,刚好e属于Null ( A^T )。
我们再来看整个过程,把列空间记为R(A) ,左零空间记为N(A*)。
那么, 就可以把b-Ax也投影到这两个空间中。
因为
并且
, 所以两者之差也属于列空间。
在根据
两个空间垂直, 那么我们根据勾股定理:
因此, 如果我们找到x刚好投影到bR, 那么直接得到如下表达式。
这样,我们要最小化 b-Ax 的模,等价于最小化bN, 而前面已经说明了bN是投影最小了。
那么如何求解这个x呢? 我们把Ax = bR代入进去:
然后在根据左零空间的性质, 两边左成A*(A的转置)
这样我们得到:
这样我们通过几何含义得到了和最小二乘法代数求解一样的结论。
我们再从代数的角度来验证一下整个流程。 根据结论:
那么可以得到
那么, 展开
那么, 我们知道最小值达到的情况就是让第一项为零。
再总结一下整个流程, 任意一个向量Ax=b, 因为b不属于Col(A),所以无解, 因此需要分解到Col(A)一个分量求解, 但是要求另外一个分量e最小。
LS, 最小二乘法的 扩展
偏差的扩展 (offsets)
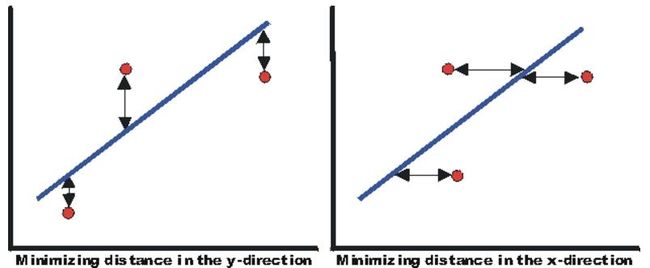
前面在几何意义时候说了, 标准的最小二乘法是竖直的偏差Vertical Offsets。
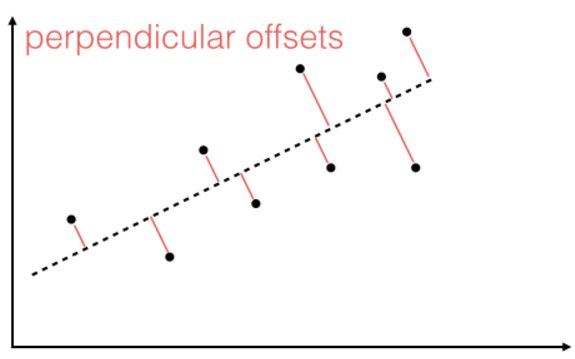
垂直偏差 (Perpendicular )
除了标准的最小二乘法外, 还有更多扩展, 譬如垂直的偏差Perpendicular Offsets。 垂直偏差的目标公式比较简单, 直接基于竖直边和垂直边的比例为1+b^2 : 1来进行处理。
水平偏差 (Horizontal )
甚至还有水平偏差horizontal offsets。
对于这种情况, 需要把目标公式修改成如下:
这里我们着重解释了一下目标公式, 有了目标公式, 求解一般来说就是拉格朗日Larange问题了。
权重的扩展
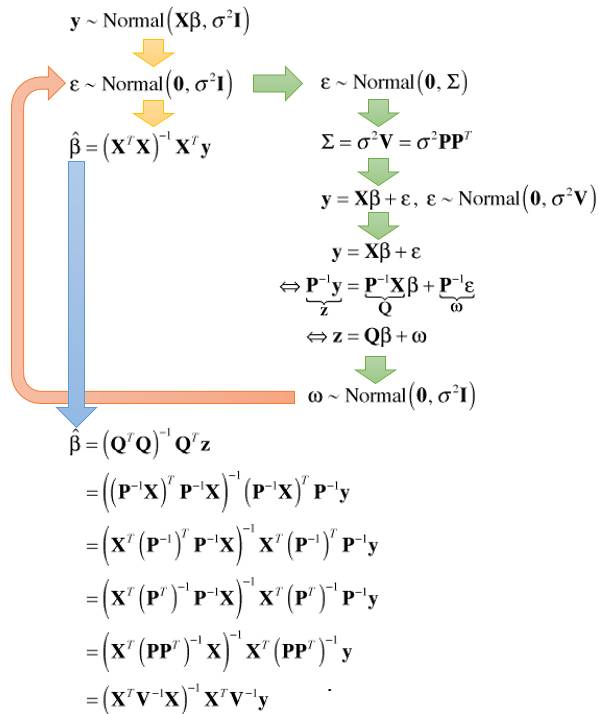
带权重Weighted LS, WLS是广义Generalized Least Squares, GLS的一个特例, 根据前面提到的,最小二乘法同正态分布的关系。 可以很容易得到一般解, 当把误差的分布修改成协方差情况, 就是带权重的最小二乘法了,通过分解替换, 又可以得到一般的LS, 这样再把替换直接代入结论, 就得到GLS的解了。
非线性扩展
大部分扩展都是利用泰勒(Taylor)公式来做不可解部分的近似,所以基本两个要点:
求解 参数变化(Δ θ): 因为非线性, 你不能求解出θ的完整解(Close form), 所以你求解目标变成了求解小的变化量
通过 Taylor 求解导数: 因为前面参数求导用的是Δ θ,所以目标表达式也会利用Taylor展开,基于上一次的目标量Δ f( θ (k+1) ) = f'(θ (k))
对于非线性Non-linear LS, NLS来说, 也是类似的, 在目标一致的情况, 首先对Δ θ和Δ f进行构建。
其次, 将目标里面的部分进行改写。
最后进行目标求解:
同时还可以进行加权扩展(Weighted)。
需要注意的是, 对于矩阵的一阶导数,Jacobbian矩阵, 和二阶导数Hessian矩阵,会经常遇到, 形式如下:
小结,从高斯说起, 我们描述了最小二乘法(LS)的由来和一般性扩展。 下次, 我们会讲述线性规划(Linear Programming, LP)的问题, 再次强调, 我们主要介绍概念的东西。
参考:
http://www.weibull.com/hotwire/issue10/relbasics10.htm
http://mathworld.wolfram.com/LeastSquaresFittingPerpendicularOffsets.html
https://www.unc.edu/courses/2010spring/ecol/562/001/docs/lectures/lecture9.htm