LeetCode 352. Data Stream as Disjoint Intervals
Description
Given a data stream input of non-negative integers a1, a2, ..., an, ..., summarize the numbers seen so far as a list of disjoint intervals.
For example, suppose the integers from the data stream are 1, 3, 7, 2, 6, ..., then the summary will be:
[1, 1]
[1, 1], [3, 3]
[1, 1], [3, 3], [7, 7]
[1, 3], [7, 7]
[1, 3], [6, 7]
Follow up:
What if there are lots of merges and the number of disjoint intervals are small compared to the data stream's size?
NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.
描述
给定一个非负整数的数据流输入 a1,a2,…,an,…,将到目前为止看到的数字总结为不相交的区间列表。
例如,假设数据流中的整数为 1,3,7,2,6,…,每次的总结为:
[1, 1]
[1, 1], [3, 3]
[1, 1], [3, 3], [7, 7]
[1, 3], [7, 7]
[1, 3], [6, 7]
进阶:
如果有很多合并,并且与数据流的大小相比,不相交区间的数量很小,该怎么办?
思路
- 把一个数插入到区间中,如果这个数与某个区间的头部(或尾部)相差 1,那么这个区间就应当被扩大。
- 如对于已经存在的区间如[[1,3],[6,9]],向里面插入 4,由于 4 和 第一个区间的末尾 3 相差 1,于是第一个区间被扩大,结果为[[1,4],[6,9]]。
- 对于区间 [[1,4],[6,9]],向里面插入 5 ,由于 5 和第一个区间末尾相差1,与 第二个区间的头部相差1,于是 5 把这两个区间连在了一起,结果为 [[1,9]]。
- 用 added 存储已经用过形成区间的数字,num_bisect 存储下一次需要用于形成区间的数字,invs 存储所有的区间。
- 我们要做的就是依次将 num_bisect 中的数字 num 添加到区间中,则有如下情况:
- 如果 num 已经出现在了 added 中,说名此数已经形成了区间,继续下一个循环;
-
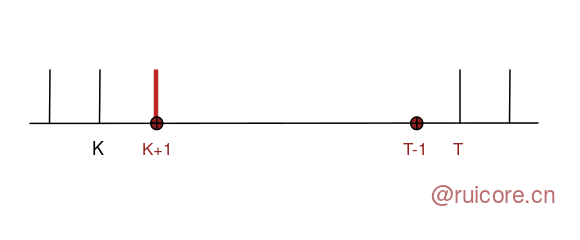
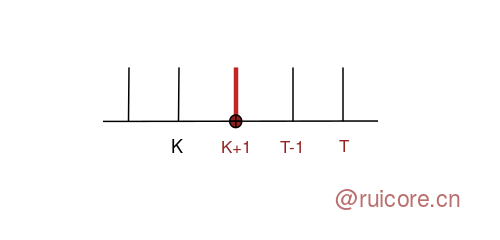
如果 num 比区间 i 的右边界大 1,如下图 1,那么区间 i 需要扩大右边界,如果此时刚好 num 比 区间 i+1 的左边界小 1,那么需要将 区间 i 和 i+1 合并,如图 2;
-
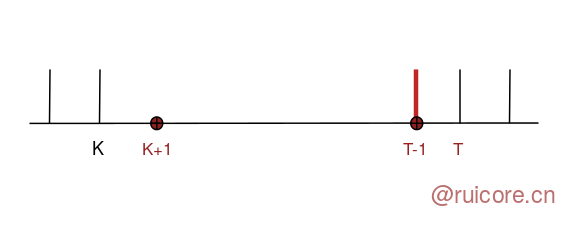
如果 num 比区间 i 的左边界小 1,如图 3,那区间 i 需要扩大左边界(这里不用考虑合并两个去区间的问题,因为在情况 2 中会会被合并)
-
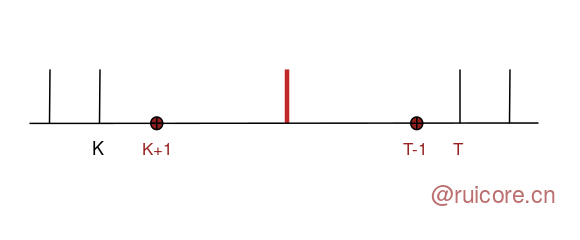
如果 num 没有与任意一个区间短点相差 1,则创建新的区间。
# -*- coding: utf-8 -*-
# @Author: 何睿
# @Create Date: 2019-06-01 16:53:14
# @Last Modified by: 何睿
# @Last Modified time: 2019-06-01 18:25:18
import bisect
from typing import List, Dict, Set
class SummaryRanges(object):
def __init__(self):
"""
Initialize your data structure here.
"""
self.added = set() # type:Set([int])
self.num_bisect = list() # type:List[int]
# 第一个区间初始化为 -2,或者比 -2 更小的数
self.invs = [[-2, -2]] # type:List[List[int]]
def addNum(self, val: int) -> None:
# 如果 val 已经被添加过,那么不用再次添加
if val in self.added: return
self.added.add(val)
# 用 bisect 将数字插入到数组中,为下一次生成区间做准备
# 在这里使用 insort_left 或 insort_right 效果一样
bisect.insort_left(self.num_bisect, val)
def getIntervals(self) -> List[List[int]]:
# 外层循环,为每一个 num 找到其应该落在的区间
for num in self.num_bisect:
# 内层循环,遍历每一个区间
for i in range(len(self.invs)):
# 如果 num 在区间 invs[i] 的内部,则什么都不做
if self.invs[i][0] < num < self.invs[i][1]:
break
# 如果 num 在区间的 self.invs[i] 的右边一个
# 则扩充 self.invs[i] 区间
elif num == self.invs[i][1] + 1:
self.invs[i][1] += 1
# 如果 self.invs[i] 后面还有区间
# 并且 num 和 self.invs[i+1]的左边界相差 1
# 将区间 self.invs[i] 与 self.invs[i+1]合并,删除 self.invs[i+1]
if i + 1 < len(self.invs):
if self.invs[i + 1][0] == num + 1:
self.invs[i][1] = self.invs[i + 1][1]
del self.invs[i + 1]
break
# 如果 num 在区间的 self.invs[i] 的左边一个
# 扩充左区间
elif num + 1 == self.invs[i][0]:
self.invs[i][0] = num
break
else:
# 如果 num 比前一个区间的尾部值大并到了最后一个位置
if i + 1 == len(self.invs) and num > self.invs[i][1] + 1:
self.invs.append([num, num])
break
# 如果 num 比前一个区间的尾部值大比后一个区间前部值小
elif self.invs[i][1] + 1 < num < self.invs[i + 1][0] - 1:
self.invs.insert(i + 1, [num, num])
self.num_bisect = list()
return self.invs[1:]
源代码文件在 这里 。
©本文首发于 何睿的博客 ,欢迎转载,转载需保留 文章来源 ,作者信息和本声明.