LeetCode 1292 Maximum Side Length of a Square

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

Example 1:

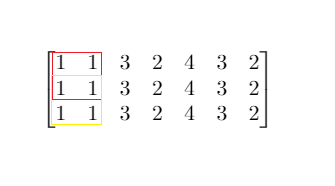
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

输入一个二维数组mat和一个整数treshold.
二维数组代表一个矩形，对于其中的正方形，（正方形所包含的点的和值小于等于treshold），返回最大的那个正方形的边长。
方法1：暴力搜索。

// O(m*n*min(m,n))
public int maxSideLength(int[][] mat, int threshold) {
    int m = mat.length, n = mat[0].length;
    int[][] dp = new int[m + 1][n + 1];
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
        }
    }
    int ans = 0;
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            for (int k = 0; i + k <= m && j + k <= n; k++) {
                // 计算矩形面积
                int area = rangeSum(i, j, i + k, j + k, dp);
                if (area > threshold) break;
                ans = Math.max(ans, k + 1);
            }
        }
    }
    return ans;
}

// 求以[x1, y1]点为左上角，[x2, y2]点为右下角的矩形的面积
private int rangeSum(int x1, int y1, int x2, int y2, int[][] dp) {
    return dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];
}

把k初始化时，直接替换成ans，可以把时间复杂度降低为平方级。

再看binary search方法：

class Solution {
    // O(m*n*lg(min(m,n))
    public int maxSideLength(int[][] mat, int threshold) {
        int m = mat.length, n = mat[0].length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        int ans = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // 可以用binary search 把时间复杂度从m*n*min(m,n)降为m*n*lg(min(m,n))
                int left = 0, right = Math.min(m - i, n - j) + 1;
                while (left < right) {
                    int mid = left + (right - left) / 2;
                    if (rangeSum(i, j, i + mid, j + mid, dp) > threshold) {
                        right = mid;
                    } else {
                        left = mid + 1;
                    }
                }
                ans = Math.max(ans, left);
            }
        }
        return ans;
    }

    // 求以[x1, y1]点为左上角，[x2, y2]点为右下角的矩形的面积
    private int rangeSum(int x1, int y1, int x2, int y2, int[][] dp) {
        return dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1];
    }
}

https://zxi.mytechroad.com/blog/dynamic-programming/leetcode-1292-maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold/