学习资料:
- 爱哥自定义控件其实很简单5/12
- 徐医生贝塞尔曲线开发的艺术
十分感谢两位大神 :)
1. Bezier
Bezier是一个法国的数学家的名字。在Path中,lineTo()方法是用来绘制直线的,quadTo()和cubicTo()来绘制曲线
Bezier原理就是利用多个点的位置来确定出一条曲线。这多个点就是起点,终点,控制点。控制点可以没有,也可以有多个。个人感觉,除了这些必要的点外,还可以虚拟出一个运动点
曲线可以看作是一个运动点的轨迹。在高中时,数学大题中,往往会有一道让求一个点的运动轨迹,一般结果是一个椭圆或者圆的数学公式。Bezier的绘制曲线,感觉也就是这个运动点的运动轨迹
1.1 一阶贝塞尔曲线
没有控制点,一阶贝塞尔曲线
这时,只有起点P0和終点P1,运动点在P0,P1间的运动轨迹就是一条线段
公式:
B(t)就是运动点在t时刻的坐标,p0起点,p1终点
对应的就是lineTo()方法
图和公式来自爱哥的博客
1.2 二阶贝塞尔曲线
一个控制点,二阶贝塞尔曲线
起点P0和終点P2,控制点就是P1,运动点在P0,P1,P2三个点的约束下,运动形成的轨迹就是红色的曲线
公式:
二阶对应的方法就是quadTo()
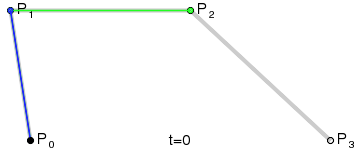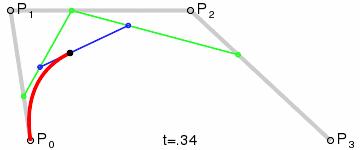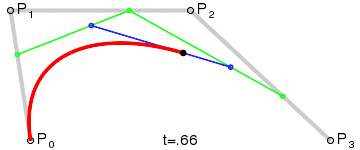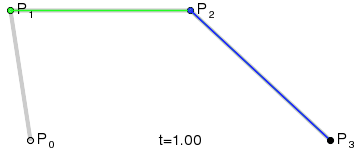
1.3 三阶贝塞尔曲线
两个个控制点,三阶贝塞尔曲线
红色就是运动点的轨迹,也就是最终会绘制的曲线
公式:
三阶对应的方法就是cubicTo()
幸亏Path类对计算过程做了封装 : )
2. 模拟向杯子中倒水
主要的思路,就是起点,终点,控制点的Y坐标不断减小,屏幕顶部的``Y轴坐标为0,向屏幕上方偏移,也就是水位上升。在水位上升的同时,控制点X轴不断变化,产生水波浪左右涌动的感觉;还要将水位线下方的区域用mPath.close()`闭合,这样才会有种水不断在杯子中增多的感觉
代码:
public class BezierView extends View {
private Paint mPaint;
private Path mPath;
private Paint paint;
private int viewWidth, viewHeight; //控件的宽和高
private float commandX, commandY; //控制点的坐标
private float waterHeight; //水位高度
private boolean isInc;// 判断控制点是该右移还是左移
public BezierView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
/**
* 初始化画笔 路径
*/
private void init() {
//画笔
mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
mPaint.setColor(Color.parseColor("#AFDEE4"));
//路径
mPath = new Path();
//辅助画笔
paint = new Paint(Paint.ANTI_ALIAS_FLAG);
paint.setColor(Color.RED);
paint.setStrokeWidth(5f);
}
/**
* 获取控件的宽和高
*/
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
viewWidth = w;
viewHeight = h;
// 控制点 开始时的Y坐标
commandY = 7 / 8f * viewHeight;
//终点一开始的Y坐标 ,也就是水位水平高度 , 红色辅助线
waterHeight = 15 / 16F * viewHeight;
}
/**
* 绘制
*/
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
// 起始点位置
mPath.moveTo(-1 / 4F * viewWidth, waterHeight);
//绘制水波浪
mPath.quadTo(commandX, commandY, viewWidth + 1 / 4F * viewWidth, waterHeight);
//绘制波浪下方闭合区域
mPath.lineTo(viewWidth + 1 / 4F * viewWidth, viewHeight);
mPath.lineTo(-1 / 4F * viewWidth, viewHeight);
mPath.close();
//绘制路径
canvas.drawPath(mPath, mPaint);
//绘制红色水位高度辅助线
canvas.drawLine(0,waterHeight,viewWidth,waterHeight,paint);
//产生波浪左右涌动的感觉
if (commandX >= viewWidth + 1 / 4F * viewWidth) {//控制点坐标大于等于终点坐标改标识
isInc = false;
} else if (commandX <= -1 / 4F * viewWidth) {//控制点坐标小于等于起点坐标改标识
isInc = true;
}
commandX = isInc ? commandX + 20 : commandX - 20;
//水位不断加高 当距离控件顶端还有1/8的高度时,不再上升
if (commandY >= 1 / 8f * viewHeight) {
commandY -= 2;
waterHeight -= 2;
}
//路径重置
mPath.reset();
// 重绘
invalidate();
}
/**
* 测量
*/
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
int wSpecMode = MeasureSpec.getMode(widthMeasureSpec);
int wSpecSize = MeasureSpec.getSize(widthMeasureSpec);
int hSpecMode = MeasureSpec.getMode(heightMeasureSpec);
int hSpecSize = MeasureSpec.getSize(heightMeasureSpec);
if (wSpecMode == MeasureSpec.AT_MOST && hSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(300, 300);
} else if (wSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(300, hSpecSize);
} else if (hSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(wSpecSize, 300);
}
}
}
起始点坐标为(-1 / 4F * viewWidth, waterHeight)
控制点(commandX, commandY)
终点(viewWidth + 1 / 4F * viewWidth, waterHeight)
起始点和终点的X轴超出了BezierView控件的大小,是为了让水波浪看起来更加自然
3. 纸飞机
将贝塞尔曲线和属性动画结合使用,使飞机曲线飞行
3.1 De Casteljau 德卡斯特里奥算法
二阶计算公式:
B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1]
-
t曲线长度比例 -
p0起始点 -
P1控制点 -
P2终止点
public static PointF calculateBezierPointForQuadratic(float t, PointF p0, PointF p1, PointF p2) {
PointF point = new PointF();
float temp = 1 - t;
point.x = temp * temp * p0.x + 2 * t * temp * p1.x + t * t * p2.x;
point.y = temp * temp * p0.y + 2 * t * temp * p1.y + t * t * p2.y;
return point;
}
三阶计算公式:
B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3, t ∈ [0,1]
-
t曲线长度比例 -
P0起始点 -
P1控制点1 -
P2控制点2 -
P3终止点
public static PointF calculateBezierPointForCubic(float t, PointF p0, PointF p1, PointF p2, PointF p3) {
PointF point = new PointF();
float temp = 1 - t;
point.x = p0.x * temp * temp * temp + 3 * p1.x * t * temp * temp + 3 * p2.x * t * t * temp + p3.x * t * t * t;
point.y = p0.y * temp * temp * temp + 3 * p1.y * t * temp * temp + 3 * p2.y * t * t * temp + p3.y * t * t * t;
return point;
}
关于这个算法,可以在看看德卡斯特里奥算法——找到Bezier曲线上的一个点
3.2 纸飞机代码
使用属性动画,需要用到估值器,估值器中需要计算飞机的飞行轨迹上的每一个点的坐标,用到了De Casteljau算法
估值器代码:
public class BezierEvaluator implements TypeEvaluator {
private PointF mPointF;
public BezierEvaluator(PointF mPointF) {
this.mPointF = mPointF;
}
@Override
public PointF evaluate(float fraction, PointF startValue, PointF endValue) {
return calculateBezierPointForQuadratic(fraction, startValue, mPointF, endValue);
}
/**
* B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1]
*
* @param t 曲线长度比例
* @param p0 起始点
* @param p1 控制点
* @param p2 终止点
* @return t对应的点
*/
private PointF calculateBezierPointForQuadratic(float t, PointF p0, PointF p1, PointF p2) {
PointF point = new PointF();
float temp = 1 - t;
point.x = temp * temp * p0.x + 2 * t * temp * p1.x + t * t * p2.x;
point.y = temp * temp * p0.y + 2 * t * temp * p1.y + t * t * p2.y;
return point;
}
}
自定义View代码:
public class PaperFlyView extends View implements View.OnClickListener {
private Bitmap flyBitmap;
private float flyX, flyY;
private float commandPointX, commandPointY; //控制点坐标
private float startPointX, startPointY; //动画起始位置
private float endPointX, endPointY;//动画结束位置
public PaperFlyView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
private void init() {
Bitmap bitmap = BitmapFactory.decodeResource(getResources(), R.drawable.paperfly);
Matrix m = new Matrix();
m.setScale(0.125f, 0.125f);
flyBitmap = Bitmap.createBitmap(bitmap, 0, 0, bitmap.getWidth(), bitmap.getHeight(), m, false);
bitmap.recycle();
//控制点 坐标
commandPointX = 1080;
commandPointY = 1080;
//设置点击监听
setOnClickListener(this);
}
/**
* 拿到控件的宽和高后 根据宽高设置绘制位置,动画开始,结束位置
*/
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
super.onSizeChanged(w, h, oldw, oldh);
flyX = 2 * flyBitmap.getWidth();
flyY = h - 3 * flyBitmap.getHeight();
//动画开始位置
startPointX = flyX;
startPointY = flyY;
//动画结束位置
endPointX = w / 2 - flyBitmap.getWidth();
endPointY = 3 * flyBitmap.getHeight();
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawBitmap(flyBitmap, flyX, flyY, null);
}
/**
* 点击事件
*/
@Override
public void onClick(View v) {
//估值器
BezierEvaluator bezierEvaluator = new BezierEvaluator(new PointF(commandPointX, commandPointY));
//设置属性动画
PointF startPointF = new PointF(startPointX, startPointY);
PointF endPointF = new PointF(endPointX, endPointY);
ValueAnimator anim = ValueAnimator.ofObject(bezierEvaluator, startPointF, endPointF);
anim.setDuration(1000);
//在动画过程中,更新绘制的位置 位置的轨迹就是贝塞尔曲线
anim.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator valueAnimator) {
PointF point = (PointF) valueAnimator.getAnimatedValue();
flyX = point.x;
flyY = point.y;
invalidate();
}
});
anim.setInterpolator(new AccelerateDecelerateInterpolator());//加速减速插值器
anim.start();
}
/**
* 测量
*/
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
int wSpecMode = MeasureSpec.getMode(widthMeasureSpec);
int wSpecSize = MeasureSpec.getSize(widthMeasureSpec);
int hSpecMode = MeasureSpec.getMode(heightMeasureSpec);
int hSpecSize = MeasureSpec.getSize(heightMeasureSpec);
if (wSpecMode == MeasureSpec.AT_MOST && hSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(300, 300);
} else if (wSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(300, hSpecSize);
} else if (hSpecMode == MeasureSpec.AT_MOST) {
setMeasuredDimension(wSpecSize, 300);
}
}
}
代码中控制点,属性动画开始和结束的点,都是随意设置的
补充 3.3
在3.2中,只有动画开启,却并没有处理动画关闭。如果动画的时间比较久,当动画运行了一半,View所在的Actiivty被关掉,还是需要考虑将动画关闭的,不及时处理,可能会造成内存泄露
@Override
protected void onDetachedFromWindow() {
super.onDetachedFromWindow();
if (null != anim && anim.isRunning()){
anim.cancel();
}
}
当View所在的Activity关闭或者View被remove掉,会调用onDetachedFromWindow()方法。对应的便是onAttachectedToWindow()方法,当View所在的Activity启动时,会调用
4.最后
学习过程基本就是严重借鉴爱哥和徐医生两个大神博客中的案例,修改
使用贝塞尔曲线,个人感觉基本思想就是确定约束点:起点,控制点,终点。中间的计算过程尽量交给Path
本人很菜,有错误,请指出
共勉 : )