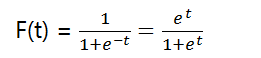本文主要介绍逻辑回归的基本概念,并结合实际案例说明逻辑回归的应用。
从线性回归到逻辑回归
在【机器学习系列2——线性回归】和【机器学习系列3——多项式回归】中我们结合实际案例解释了线性回归的基本概念和应用。线性回归解决的是连续型数值的预测问题,例如预测房价,产品销量等。
但是生活中存在大量的分类问题,例如:判断垃圾短息,垃圾邮件;银行判断是否给用户放贷;电商判断用户是否会喜欢某类商品,从而确定是否要推荐给用户等等;
解决以上这类问题,线性回归不再适用,我们需要采用逻辑回归(Logistic Regression)。
逻辑回归解决的是分类问题,从分类数量上看,有二项分类和多项分类。
二项分类一般是0和1,或者True和False的问题,例如预测病人是否患某种疾病;
多项分类中,分类标签比较多,例如根据歌词将歌曲分类,可以有多种类别:民谣,摇滚,轻音乐,说唱等等。我们通常把构建的用于分类的逻辑回归模型叫做分类器。
虽然机器学习算法中还有很多其他的分类算法,但逻辑回归是最常用的,也是首选的分类算法,它的原理非常简单,但是分类能力非常强大。一般我们拿到一个分类问题,都会先用逻辑回归看一下效果,然后再去尝试复杂的算法,看能否在逻辑回归的效果基础上有进一步的效果改进。
逻辑回归基本概念
假设t为连续随机变量,则t服从逻辑分布是指,它具有下列分布函数(Sigmoid函数):
该公式包含两个关键的部分:
- 指数变换:将所有的数值转换为正数,即e^t
- 归一化:将所有数值转换为0到1之间的数值,即1/(1+t)
所以逻辑函数输出的,是0到1之间的数值,表示的是一个概率。
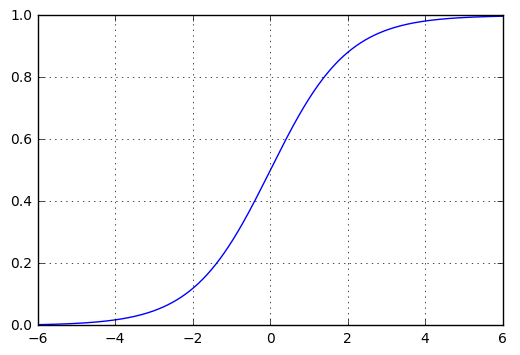
我们可以用Python看一下逻辑分布函数的图形化表示。
由于 t = 6的时候,逻辑分布函数 f(t) 的值趋近于1,t = -6时,f(t) 的值趋近于0,因此我们观察 t = {-6,6} 范围内的逻辑分布函数图形:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(-6,6,0.01)
y = np.exp(x)/(1 + np.exp(x))
plt.figure()
plt.axis([-6,6,0,1])
plt.grid(True)
plt.plot(x, y)
plt.show()
一般化逻辑回归模型
我们一般定义逻辑回归模型的预测函数如下:
其中:
其实这就是我们的一元线性回归模型;一元线性回归的输出结果取值范围是负无穷到正无穷,把它的输出结果,当做逻辑回归模型的输入,我们就把数值问题,映射为了(0,1)之间的数值,从而转换成为了分类问题(0还是1),即求y=1的概率问题(一般概率大于0.5,分类为1,概率小于0.5,分类为0)。
二项逻辑回归模型
所谓二项逻辑回归,就是y的取值只有两种可能:我们一般分别用0和1表示。
它的模型表示如下:
也即整合后的模型:
只要计算出θ参数的值,我们就能根据输入x来分别计算y = 0和y=1的概率,根据概率大小,就可以判断x应该归类到0还是1。
一般我们可以简化二项逻辑回归模型,用基本的逻辑回归模型表示:
案例
假设我们有一个样本大小为50的GPA成绩和录取与否的样本数据,我们希望通过逻辑回归,根据GPA成绩预测学生是否能被录取。数据样例如下所示,其中【gpa】是介于0到5之间的数值,表示学生的GPA成绩,【Admission】0代表没有录取,1代表被录取:
| ID | gpa | Admission |
|---|---|---|
| 1 | 3.177 | 0 |
| 2 | 3.412 | 0 |
| 3 | 2.728 | 0 |
| 4 | 4.523 | 1 |
| 5 | 3.781 | 1 |
数据基本信息探索:
我们使用Scikit-learn的linear_model中的LogisticRegression来做逻辑回归。
from sklearn.linear_model import LogisticRegression
from sklearn.cross_validation import train_test_split, cross_val_score
#读取数据
data = pd.read_csv('admissions.csv')
#拆分训练集和测试集
xtrain, xtest, ytrain, ytest = train_test_split(data['gpa'], data['Admission'])
x_train = xtrain.reshape(len(xtrain),1)
y_train = ytrain.reshape(len(ytrain),1)
x_test = xtest.reshape(len(xtest),1)
y_test = ytest.reshape(len(ytest),1)
#初始化模型
lor = LogisticRegression()
#拟合
lor.fit(x_train, y_train)
#预测,其中predict预测函数返回标签数值,即0或者1,predict_proba函数返回概率数值,即标签为0的概率和标签为1的概率,它是基于默认的0.5为阈值,概率大于0.5,标签为1,概率小于0.5,标签为0
pred_label = pd.DataFrame(lor.predict(x_test), columns=['label'])
pred_proba = pd.DataFrame(lor.predict_proba(x_test), columns=['proba_0', 'proba_1'])
#数据合并
gpa = pd.DataFrame(x_test, columns=['gpa'])
admission = pd.DataFrame(y_test, columns=['admission'])
pd.concat([gpa, admission, pred_label, pred_proba], axis = 1)
最终预测所得结果如下:
模型效果评估
二项分类模型效果的评估方法有很多,常用的有准确率(accuracy),精确率(precision),召回率(recall),ROC(Receiver Operating Characteristic),AUC(Area Under the Curve)。
准确率
准确率 = 正确预测数 / 测试集样本数
在上面的栗子中,我们的测试集样本数 = 13,其中正确预测的(admission = label)有8个,所以这里准确率 = 8 / 13 = 0.61538461538461542
我们也可以用Scikit-learn中自带的方法来计算准确率:
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(admission, pred_label)
但是准确度只能用来评估模型在测试集上的准确度,无法评估非测试集的预测准确度。
精确率
首先来看一下,在二项分类问题中,我们可以将观察值和预测值的关系用以下混淆矩阵表示出来:
精确率 = TP / (TP + FP)
在上面的栗子中,精确率指的是,在预测出来的被录取学生人数中,有多少是真正被录取的。所以测试集反映出的 精确率 = 7/12 = 0.5833333333333334
召回率
召回率在医学领域也叫做灵敏度(Sensitivity),它反映的是在模型识别阳性结果(Positive Result)的效果。
召回率 = TP / (TP + FN)
在上面的栗子中指的是,在正真被录取的学生人数中,被正确正确预测出来的人数。所以测试集反映的 召回率 = 7/7 = 1。
可以看出,精确率和召回率各自含有的信息都很少,它们对分类器效果的观察角度不同。精确率和召回率都不能从表现差的一种分类器中区分出好的分类器。
Scikit-learn中提供了计算精确率和召回率的计算函数,我们介绍使用方法之前,顺便介绍一下K折交叉验证(K-Fold Cross Validation)。
我们在【机器学习系列1——机器学习概况】中介绍到,在数据集本身非常少,可能存在训练集不够而无法很好的构建模型的情 况下,可以使用交叉验证方法。主体思想就是将数据集分成K等份,用其中K-1份做训练,剩余1份做测试,然后依次迭代。如下图所示,这里K=5。
在数据集非常大的情况下,数据集拆分不宜过多,否则迭代将耗费太多时间。
Scikit-learn提供了K折交叉验证所需要的函数KFold,可以直接调用。
下面我们结合K折交叉验证,来说明二项分类逻辑回归中的精确率和召回率的计算。
from sklearn.cross_validation import KFold
from sklearn.cross_validation import cross_val_score
#shuffle = True表示打乱数据集顺序,random_state = 1表示在shuffle设置为True的时候,随机种子的值,相当于如果设置该值,每次执行代码时,数据集的拆分结果都是固定的,如果不设置,每次数据集的拆分都是随机的,计算所得结果也会有差异
kf = KFold(len(data), 5, shuffle = True,random_state = 1)
accuracy = cross_val_score(lor, data[['gpa']], data['Admission'], cv = kf, scoring = 'accuracy')
recall = cross_val_score(lor, data[['gpa']], data['Admission'], cv = kf, scoring = 'recall')
precision = cross_val_score(lor, data[['gpa']], data['Admission'], cv = kf, scoring = 'precision')
print('准确率:', accuracy.mean(), accuracy)
print('精确率:', precision.mean(), precision)
print("召回率:", recall.mean(), recall)
所得结果为:
准确率: 0.68 [ 1. 0.3 0.5 0.9 0.7]
精确率: 0.677777777778 [ 1. 0.22222222 0.5 0.83333333 0.83333333]
召回率: 0.942857142857 [ 1. 1. 1. 1. 0.71428571]
由于这里采用了交叉验证,和之前计算的精确率结果稍有差异。
综合评价指标(F-measure)
一般情况下,我们希望精确率和召回率都越高越好,但在一些极端情况下,两者是矛盾的。这时候我们需要用综合评价指标:精确率和召回率的调和均值(harmonic mean),或加权平均值,也称为F-measure或F-score。
F-measure = 2 * Precision * Recall / (Precision + Recall)
F-measure 平衡了精确率和召回率。当F-measure较高的时候,说明模型效果比较好。
Scikit-learn中提供了直接计算F-measure的方法:
f1 = cross_val_score(lor, data[['gpa']], data['Admission'], cv = kf, scoring = 'f1')
综合评价指标: 0.741724941725 [ 1. 0.36363636 0.66666667 0.90909091 0.76923077]
ROC & AUC
介绍ROC之前,需要先介绍假阳性概率(False Positive Rate),即所有阴性样本中,分类器预测出的假阳性样本的比率,也叫做误警率,FPR = FP / (TN + FP)
ROC曲线(Receiver Operating Characteristic curve,ROC curve),是以假阳性概率(误警率)为横坐标,以真阳性概率(召回率)为纵坐标所画的曲线。可以理解为它是一系列混淆矩阵的结果组合所画出的曲线。一般情况下,我们得到一个回归模型的混淆矩阵,都是在提前设定好一个阈值的前提下获得的。例如上面案例中,我们以默认的阈值0.5为界限,得到混淆矩阵如下:
| 预测值 \ 观察值 | Admitted (1) | Rejected (1) |
|---|---|---|
| Admitted (1) | 7 | 5 |
| Rejected (1) | 0 | 1 |
但如果我们调整这个阈值,得到的混淆矩阵就不同了。在模型预测的所有概率中,每一个概率值都可以作为一个阈值,相应的,我们就能得到一系列的混淆矩阵。对于每个混淆矩阵,我们都能计算出相应的假阳性概率FPR和真阳性概率TPR。然后我们以这些FPR为横坐标轴,以TPR为纵坐标轴,所得到的曲线就是ROC。
Scikit-learn中提供了ROC曲线对应的函数roc_curve,我们根据上面案例,画出对应的ROC曲线如下:
from sklearn import metrics
probabilities =lor.predict_proba(x_test)
fpr, tpr, thresholds = metrics.roc_curve(y_test, probabilities[:,1])
plt.plot(fpr, tpr)
plt.show()
因为我们测试集样本数量太少,画出来的曲线不太好看。。。
理想的情况下,如果存在一个阈值,大于这个阈值的都是阳性的,低于这个阈值的都是阴性的,那么我们认为这个模型已经能够非常完美的区分阳性和阴性了,对应到我们的案例中,就是我们找到一个回归模型,能够确定一个的阈值,高于这个阈值的都被录取了,低于这个阈值的都没有被录取,那么这个模型就是完美的。此时对应的真阳性概率TPR为1,假阳性概率FPR为0,对应坐标轴上的(0,1)点,即左上角的点。所以如果ROC曲线经过该点,它就是完美的。但事实上,现实生活中不会有这么完美的模型。
AUC(Area Under the Curve)是指ROC曲线下面的面积。从AUC定义的角度来理解,AUC就是从所有标签为1的样本中随机选取一个样本, 从所有标签为0的样本中随机选取一个样本,然后根据分类器对两个随机样本进行预测,假设标签为1的样本预测为1的概率为p1,标签为0的样本预测为1的概率为p0,那么p1>p0的概率就等于AUC。所以AUC反应的是分类器对样本的排序能力。
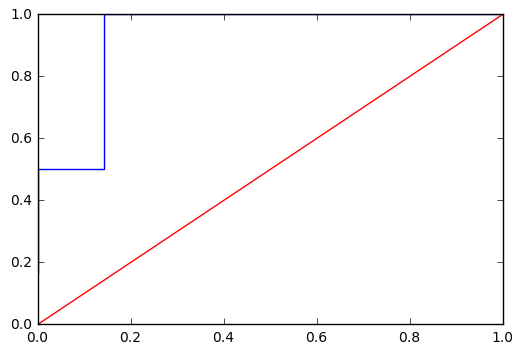
一般情况下,AUC值介于0.5和1之间,AUC值越大,说明分类器效果越好,ROC曲线越接近于(0,1)点。AUC值越小,说明分类器效果越差,跟随机分类没什么差别,ROC曲线越趋近于下图中的红线。如果AUC值小于0.5,则可能是样本数据标签出了问题。
另外值得注意的是,AUC对样本类别是否均衡并不敏感,这也是不均衡样本通常用AUC评价分类器性能的一个原因。
Python中计算AUC值的方法如下:
auc_score = metrics.roc_auc_score(y_test, probabilities[:,1])
auc_score = 0.9285714285714286