Logit模型拟合实战案例(Python)
转载链接
前言:本文详细介绍如何在Python中拟合Logit模型,包括数据准备、哑变量的处理、参数拟合结果解读等内容。
案例介绍:
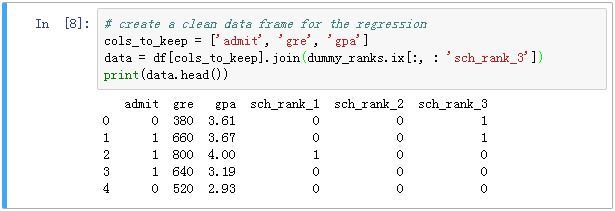
这里仍然使用和上一篇中相同的数据。我们要研究的问题是:在申请的研究生的时候,什么样的学生更容易被录取。
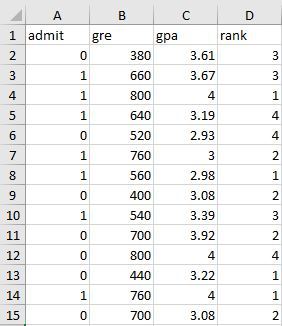
原始数据保存在名为“Application.csv”的文件中(文件格式为csv格式),每一行代表一条申请者的记录:
[图片上传失败...(image-adb16d-1563615674559)]
原始数据中包含3个自变量:
- 申请者的GRE成绩,用变量gre表示;
- 申请者的平均绩点,用变量gpa表示;
- 申请者所在的本科院校的排名,用变量rank表示。
变量gre和gpa都是连续变量。rank为离散变量,只能取1、2、3、4中的某一个值;rank=1对应的学校排名最高,而rank=4对应的排名最低。
申请的结果只有两种情形:“录取”或者“拒绝”。我们用变量admit表示申请结果,显然,admit是一个二分类的变量——admit=1表示“申请者被录取”,admit=0表示“申请者被拒绝”。
软件准备:
本例需要调用下面这几个包:
- numpy:Python中用于数值计算的包,可以方便地进行数组和矩阵的相关计算;
- pandas:利用pandas可以高效地对数据进行操作和管理;
- statsmodels:Python中用于统计建模和计量经济学的包,可以进行描述性统计、统计模型估计和推断等操作;
- pylab:本例中用于绘图。
运行Python代码之前,请确保已经正确安装相应的软件包。
建模准备:
正式建模之前,可以先做一些描述性分析(Descriptive analysis)——看一看样本中各变量的均值、方差等等,以加强对数据的理解。具体实现步骤如下。
在Python中导入相应的包:
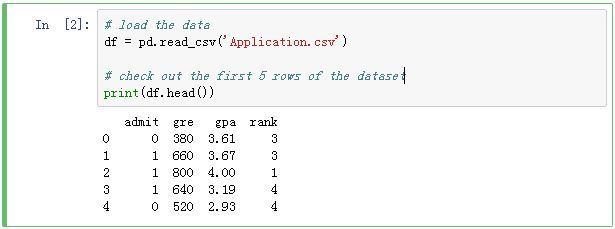
用pandas的read_csv()
函数读取原始数据文件,并展示前5行:
由于pandas的DataFrame数据结构也有一个方法的名称为rank,这容易与原始数据表中的列名rank产生混淆。将原始数据表中的列名rank更改为sch_rank:
用describe() 函数对样本中的各变量做描述性分析,结果如下面所示。我们可以得到每一个变量的出现的频数(count)、均值(mean)、标准差(std)、最大/小值(min/max)、百分位数(25%,50%,75%)等信息。这一步相当于SAS中的Proc
Means和Proc Freq。
当然,还可以做一下交叉频数分析,粗略地观察(离散的)自变量和因变量之间关系。例如,根据下图我们就可以看出:在样本中,当申请者所在的学校排名越高时(’sch_rank=1’),申请者被录取的比例也就越大。
还可以利用直方图来可视化数据:
(P.S. Python新手一枚,这图中间有点挤,各位有什么方法可以增加中间的间距么?谢谢!)
数据准备:
在Python中拟合Logit模型的过程非常简单,直接调用statsmodels库中的Logit() 函数即可。调用Logit() 函数的基本格式:
[图片上传失败...(image-9eee6f-1563615674558)]
Logit() 函数有两个输入参数:
- endog代表和因变量(Y)对应的数据,通常为一维的数组;本例中就是原始数据中和变量admit相对应的那一列数据:
- exog代表和自变量(X)对应的数据;本例中就是变量gre、gpa、rank(后更名为sch_rank)相对应的那一部分数据:
问题在于——
(1)变量sch_rank是一个分类变量,需要对其进行哑变量处理。在SAS中,分类变量的哑变量化是通过 class 语句实现的(如下图),而在Python中这一步需要手动实现。
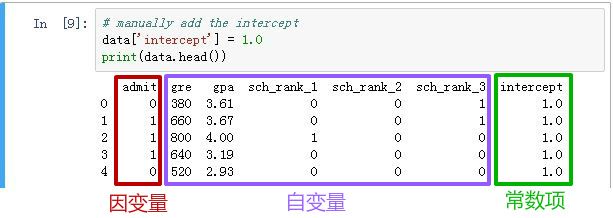
(2)Logit()函数不会自动添加常数项[1],因此我们在准备数据的时候,需要手动添加常数项。
可见,知道了Python中利用Logit() 函数就可以拟合Logit模型后,剩余工作的难点在于数据的准备。
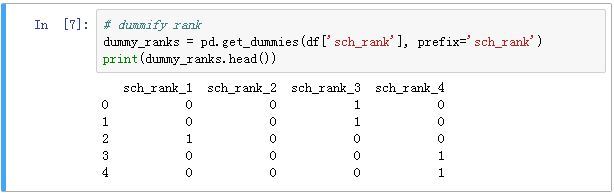
利用pandas中的get_dummies()
函数对分类变量sch_rank进行哑变量化操作,其结果是得到sch_rank_1、sch_rank_2、sch_rank_3、sch_rank_4四个0-1变量:
由于sch_rank_1 + sch_rank_2 + sch_rank_3 + sch_rank_4 =
1, 所以不能直接把这四个变量同时放到模型(否则会有共线性的问题),我们选取sch_rank_4作为基变量(和上一篇的SAS案例保持一致),把sch_rank_1、sch_rank_2、sch_rank_3和其它两个自变量gre、gpa的数据拼到一起:
手动添加常数项:
至此,数据准备工作已经完成!
模型拟合:
在拟合Logit模型的时候,只要从上面的data中提取出因变量、自变量(含常数项)相对应的列,然后放到Logit()函数中即可。
提取和自变量、常数项相对应的列名:
拟合Logit模型。拟合的结果存储于result对象中:
输出result对象中的拟合结果:
上表中输出了Logit模型的相关拟合结果。结果包含两部分:上半部分给出了和模型整体相关的信息,包括因变量的名称(Dep. Variable: admit)、模型名称(Model: Logit)、拟合方法(Method: MLE 最大似然估计)等信息;下半部分则给出了和每一个系数相关的信息,包括系数的估计值(coef)、标准误(std err)、z统计量的值、显著水平(P>|z|)和95%置信区间。
根据上表可以得到本例中Logit模型的具体形式:
由于哑变量sch_rank_3的值并不显著(0.591),因此sch_rank_3没有包含在上面的模型中。
在Logit模型中,变量的系数是指:自变量每变化一个单位,胜率(Odds)的对数的变化值。在本例中,以变量gre的系数为例,其解读方式为:
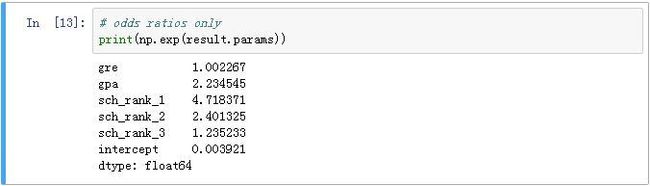
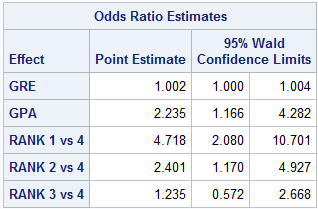
求各系数的指数值(即相应的Odds):
也可输出和Odds相对应的95%置信区间:
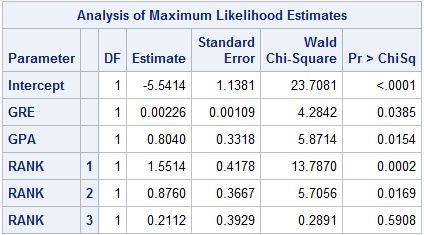
我们可以将Python中输出的结果和SAS中的结果(见下图)进行对比——二者的系数估计结果基本一致(一个细小的区别是:在检验单个变量是否显著时,statsmodels用的是z统计量,SAS用的是Wald Chi-Square 统计量)。