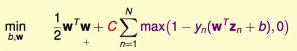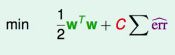本文参考整理了Coursera上由NTU的林轩田讲授的《机器学习技法》课程的第五章的内容,主要介绍了SVM和logistic regression的联系及kernel logistic regression问题,如何将kernel trick应用到logistic regression在高维空间的训练和综合了SVM flavor及LogReg flavor的Two-Level Learning方法,解释了hinge error measure、probabilistic SVM、representer theorem等概念,文中的图片都是截取自在线课程的讲义。
欢迎到我的博客跟踪最新的内容变化。
如果有任何错误或者建议,欢迎指出,感激不尽!
--
本系列文章已发五章,前四章的地址如下:
- 一、线性SVM
- 二、SVM的对偶问题
- 三、Kernel SVM
- 四、Soft-Margin SVM
Soft-Margin SVM as Regularized
两个open source机器学习库
NTU的林智仁(Chih-Jen Lin)开发的针对linear SVM的LIBLINEAR和针对non-linear的dual\kernel SVM的LIBSVM库。
松弛变量ξn
注意:以后直接使用score来代表某个点在线性分类器下的得分,即score(Xn)=W’Zn+b。
给定任何一个边界(b,W),ξn = margin violation = max(1-yn(score),0)
因为一个点有两种可能:
- (Xn,yn) 确实违反了边界,则ξn = 1- yn(score) >= 0
- (Xn,yn) 没有违反边界,则ξn = 0
无约束形式
因此,可以把SVM(以后若不指明,特指使用最多的soft-margin SVM)写成以下'unconstrained'形式:
ξn不再是变量,而是根据(b,W)算出来的结果。
这个式子有点熟悉,和以前我们所做的Regularization的形式很类似:
所以我们可以把SVM看成L2 regularization,只是有很小的细节不太一样
既然是一个正则化的问题,那么为什么不直接用regularization的求解方法求解呢?
因为
- 不是QP问题,也不容易使用kernel trick
- 错误衡量里面有一个max(□,0)的操作,不可微分,很难求解
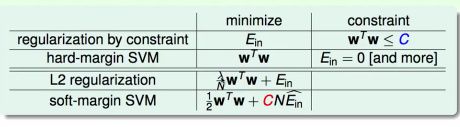
作为正则化模型的SVM
我们不难得到,C和λ的关系是large margin <==> fewer hyperplanes <==> L2 regularization of short W
soft margin <==> special err~
larger C <==> smaller λ <==> less regularization
为什么要把SVM看成regularized model?
因为我们想要把SVM延伸扩展到其他的学习模型,比如logistic regression、linear regression等。
SVM versus Logistic Regression
SVM算法中的错误衡量
设linear score s = W’ Zn + b
则
- err[0/1](s,y) = [[ ys <= 0 ]]
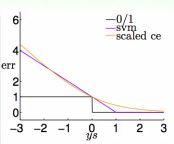
- err[svm](s,y) = max(1 - ys , 0),叫做 hinge error measure,由于它在SVM的算法中使用,也叫作algorithmic error measure,由下图可知,它是err[0/1]的一个凸的上限。
SVM和Log Reg的联系
log reg的错误衡量
- err[SCE](s,y) = log2(1+exp(-ys))
它是err[0/1]的另一个上限。
由上图可以看出,其实SVM的hinge err和Log Reg的sce err还蛮像的,从两个方向来看
| -∞ | <-- ys --> | +∞ |
|---|---|---|
| ≈-ys | err[svm](s,y) | =0 |
| ≈-ys | (ln2)*err[sce](s,y) | ≈0 |
所以SVM≈L2 regularied logistic regression
二元分类的线性模型
regularized LogReg ==> approximate SVM √
SVM ==> approximate LogReg ?
把SVM用在Soft Binary Classification
简单想法
如何把两者的特性融合在一起呢?
Two-Level Learning
SVM flavor: 通过W[svm]固定了超平面的方向-->利用了kernel
LogReg flavor: 通过LogReg的训练去微调超平面以满足最大似然性(maximum likelihood),通过A放缩和B平移。
- 通常A>0,如果W[svm]做得比较好
- 通常B≈0,如果b[svm]做得比较好
新的LogReg问题如下:
可以把W[svm]’Φ(Xn)+b[svm]看成一个特别的转换Φsvm,它是从多维转到一维的转换。
所以可以分为两个阶段学习:
- 做SVM,结果作为转换,将数据转换到1维空间
- 做1维空间内的简单的LogReg问题
Probabilistic SVM
在SVM领域,这是一个非常常用的方法,它一开始由John Platt提出,叫做Probabilistic SVM的Platt's Model。
这样得到的soft binary classifer可能和原来的SVM的结果的边界不一定一样,因为有参数B可以平移边界。
如何解LogReg?可以用梯度下降法GD、随机梯度下降法SGD或者专门的更简单的方法(因为只有两个变量)。
kernel SVM ==> approx. LogReg in Z-space
我们并没有真的在Z空间里面找LogReg最好的解,而是利用SVM与LogReg的相似性,利用SVM的kernel trick在Z空间内解SVM,再做一些AB参数的微调以使其更满足LogReg的要求。
如果我们真的要找在Z空间里面最好的LogReg的解该怎么做呢?这是我们下一小节的课题。
Kernel Logistic Regression
Kernel Trick奏效的关键
我们在SVM问题中是怎么做的?
二次规划QP->对偶->Z空间内积->kernel...
最优的W* = ∑βZn,我们才能W*’Z = ∑βZn’Z = Σβ K(Xn,X)
重点是,W能表示成一些Z的线性组合,这是我们能够用kernel的关键!
之前讨论过一些方法,它们的最佳的W可以表示成一堆Z的线性组合
那么什么时候最好的W可以被Zn线性表示呢?
Representer Theorem
反证法容易证明:
因此,任何L2-regularied的linear model都是可以被kernelized的!
Kernel Logistic Regression
问题:
一共有N个变量β,和Z空间的维度就没有关系了。
如何解呢?
这是一个关于β的无条件的最佳化问题,可以利用GD/SGD等方法求解。
这通常叫做kernel logistic regression,即根据representer theorem利用kernel trick求解L2-regularized logistic regression。
Another View about KLR
如果把KLR看成β的线性模型,则任意一个X,它都会被转换成(K(X1,X), K(X2,X), K(X3,X) ... K(Xn,X)),这是一个N维空间。
注意:和SVM中的线性组合系数α不一样,KLR中的系数β通常都不是0!
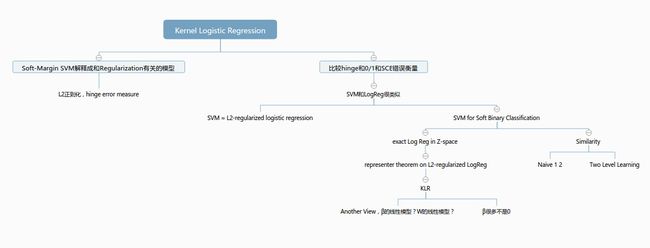
Mind Map Summary
这一章我们讲述了kernel如何应用在logistic regression问题上,下一章我们将继续探讨如何将kernel trick应用到更一般的regression上面,敬请关注!