本文实现小说翻页的基本原理
自定义View实战篇(二)实现小说翻页二实现翻页动画、阴影、内容
一、简介
首先感谢hmg25的Android 实现书籍翻页效果----原理篇,本文参考其实现,旨在巩固这方面的知识,以及为自己后面的实战做准备。
研读了实战上面的原理篇之后,我们可以知道实现翻页效果,其实是根据一些动态点进行计算,然后进行剪切,最后绘制在画布上,下面依次写出各个点的计算方法。
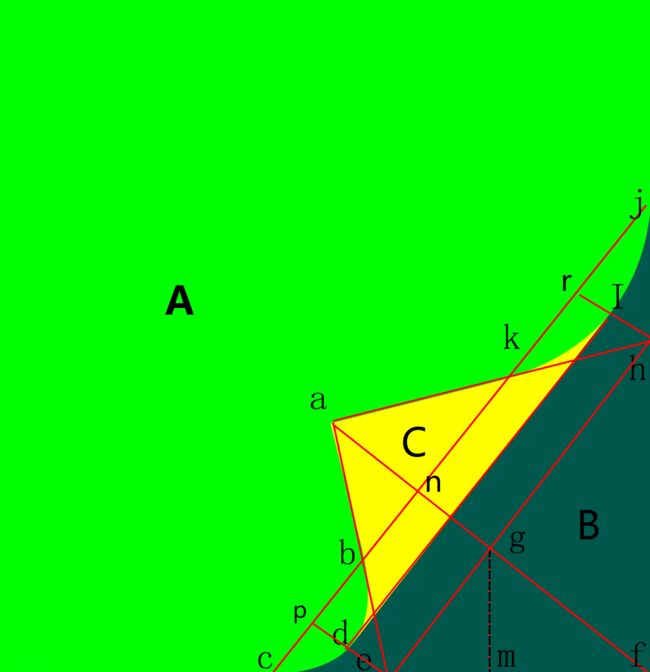
首先,我们将绿色部分称作A区域、蓝色为B区域、黄色为C区域。
a:触摸点,在onTouchonTouchEvent()中获取X、Y坐标。f:即view的大小,通过onMeasuer()获取View的宽高。-
g:g是af的中点,根据数学公式可得:g.x=(a.x+f.x)/2;g.y=(a.y+f.y)/2; -
e:根据相似三角形
egm和ggm可知,对应边成比例可得:e.x = g.x - (f.y - g.y) * ((f.y - g.y) / (f.x - g.x));e.y = f.y; -
h:同理,根据相似三角形
egf和fgh可得:h.x = f.x;
h.y = g.y - (f.x - g.x) * (f.x - g.x) / (f.y - g.y); -
c:设
n为ag中点,同理,根据相似三角形fge和fnc,且比例为1:2,可得c.x = e.x - (f.x - e.x) / 2;
c.y = f.y; -
c:设
n为ag中点,同理,根据相似三角形fgh和fnj,且比例为1:2,可得j.x = f.x;
j.y = h.y - (f.y - h.y) / 2; -
b&k:根据相似三角形abk和aeh,且比例为1:2,可得
b.x = (a.x+e.x)/2;b.y = (a.y+e.y)/2;k.x = (a.x+h.x)/2;k.y = (a.y+h.y)/2; -
p为cb的中点,d为pe的中点,所以d.x=((c.x+b.x)/2+e.x)/2
d.y=((c.y+b.y)/2+e.y)/2 r为kj的中点,d为hr的中点,所以
i.x=((k.x+j.x)/2+h.x)/2
i.y=((k.y+j.y)/2+h.y)/2
二、实现仿真翻页
1、基本实现
(1)首先,我们定义一个类保存各个点的坐标,然后由触摸点a和已知的点f获取其他坐标,由此我们通过不断获取触摸点然后配合f点坐标对各个点进行更新。
public class Point {
public float x;
public float y;
}
/**
* 计算各个点的坐标
* @param a a点的坐标
* @param f f点的坐标
*/
void calculationPoint(Point a, Point f) {
g.x = (a.x + f.x) / 2;
g.y = (a.y + f.y) / 2;
e.x = g.x - (f.y - g.y) * (f.y - g.y) / (f.x - g.x);
e.y = f.y;
h.x = f.x;
h.y = g.y - (f.x - g.x) * ((f.x - g.x) / (f.y - g.y));
c.x = e.x - (f.x - e.x) / 2;
c.y = f.y;
j.x = f.x;
j.y = h.y - (f.y - h.y) / 2;
b.x = (a.x + e.x) / 2;
b.y = (a.y + e.y) / 2;
k.x = (a.x + h.x) / 2;
k.y = (a.y + h.y) / 2;
d.x = ((c.x + b.x) / 2 + e.x) / 2;
d.y = ((c.y + b.y) / 2 + e.y) / 2;
i.x = ((k.x + j.x) / 2 + h.x) / 2;
i.y = ((k.y + j.y) / 2 + h.y) / 2;
}
(2)获取各个点坐标后,我们需要对A、B、C区域得到去Path路径
A区域计算方法:
左下角A区域我们可以从0.0出发,画直线至左下角,然后画直线到C点,然后由二次贝塞尔曲线到b点,然后画直线a点,在画直线到k点,再由二次贝塞尔曲线到j点,然后画直线到右上角最后闭合到0.0点。
mPathA.reset();
mPathA.lineTo(0, height);
mPathA.lineTo(c.x, c.y);
mPathA.quadTo(e.x, e.y, b.x, b.y);
mPathA.lineTo(a.x, a.y);
mPathA.lineTo(k.x, k.y);
mPathA.quadTo(h.x, h.y, j.x, j.y);
mPathA.lineTo(width, 0);
mPathA.close();
return mPathA;
B区域计算方法:我们只需获取整个页面的path即可,原因是因为我们翻页的位置可能是任意一个角,但是如果我们将区域B也跟随F点去判断的话,那代码将不够灵了。
mPathB.reset();
mPathB.lineTo(0, height);
mPathB.lineTo(width, height);
mPathB.lineTo(width, 0);
mPathB.close();//闭合区域
return mPathB;
C区域计算方法:C区域与A基本相同
mPathC.reset();
mPathC.moveTo(i.x, i.y);
mPathC.lineTo(d.x, d.y);
mPathC.lineTo(b.x, b.y);
mPathC.lineTo(a.x, a.y);
mPathC.lineTo(k.x, k.y);
mPathC.close();//闭合区域
return mPathC;
(3)对A、B、C根据 Path进行裁切,裁切我们要用到Canvans的clipPath方法:
clipPath由两个构造方法clipPath(Path path)、clipPath(Path path, Region.Op op)
-
op:
DIFFRENCE是第一次不同于第二次的部分显示A-B
REPLAC是显示第二次的B
REVERSE_DIFFRENCE是第二次不同于第一次的部分显示
INTERSECT是交集显示
UNION是全部显示A+B
XOR是补集(全集减去交集剩余部分)显示
A区域安装Path直接剪切
canvas.clipPath(getPathA());
B区域,先剪切A,在剪切C,然后我们设置UNION即剪切A+C的区域,然后设置REVERSE_DIFFERENCE,剪切除A+C的部分,即B的部分。
canvas.clipPath(getPathA());
canvas.clipPath(getPathC(), Region.Op.UNION);
canvas.clipPath(getPathB(), Region.Op.REVERSE_DIFFERENCE);
C区域:这里需要思考,为什么我们不直接剪切C而是先剪切A在剪切C且减去与区域A的交集部分
canvas.clipPath(getPathA());
canvas.clipPath(getPathC(), Region.Op.REVERSE_DIFFERENCE);
当然到这里我们已经可以将代码组合一下,实现最简单的翻页了。
(3)通过触摸事件,实现滑动,完整代码如下。
/**
* @author Active_Loser
* @date 2018/11/18
* Content: 自定义PageView
* A: 表示当前页面
* B: 表示上一页或下一页的页面
* C: 表示翻起的页面,即当前页的背面
*/
public class PageView extends View {
private Path mPathA;
private Path mPathB;
private Path mPathC;
private Bitmap mBitmapA;
private Bitmap mBitmapB;
private Bitmap mBitmapC;
/**
* 测量出view的宽高
*/
private int width, height;
private Point a, f, g, e, h, c, j, b, k, d, i;
public PageView(Context context) {
this(context, null);
}
public PageView(Context context, @Nullable AttributeSet attrs) {
this(context, attrs, 0);
}
public PageView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
private void init() {
a = new Point();
f = new Point();
g = new Point();
e = new Point();
h = new Point();
c = new Point();
j = new Point();
b = new Point();
k = new Point();
d = new Point();
i = new Point();
mPathA = new Path();
mPathB = new Path();
mPathC = new Path();
}
@Override
protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {
super.onMeasure(widthMeasureSpec, heightMeasureSpec);
width = getDefaultSize(600, widthMeasureSpec);
height = getDefaultSize(1000, heightMeasureSpec);
setMeasuredDimension(width, height);
f.x = width;
f.y = height;
mBitmapA = Bitmap.createBitmap(width, height, Bitmap.Config.ARGB_8888);
mBitmapB = Bitmap.createBitmap(width, height, Bitmap.Config.ARGB_8888);
mBitmapC = Bitmap.createBitmap(width, height, Bitmap.Config.ARGB_8888);
Canvas mCanvasA = new Canvas(mBitmapA);
mCanvasA.drawColor(Color.GREEN);
Canvas mCanvasB = new Canvas(mBitmapB);
mCanvasB.drawColor(Color.YELLOW);
Canvas mCanvasC = new Canvas(mBitmapC);
mCanvasC.drawColor(Color.BLUE);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
float x = event.getX();
float y = event.getY();
a.x = x;
a.y = y;
calculationPoint(a, f);
postInvalidate();
return true;
}
@Override
protected void onDraw(Canvas canvas) {
drawA(canvas);
drawC(canvas);
drawB(canvas);
}
/**
* 剪切A区域
*/
private void drawA(Canvas canvas) {
canvas.save();
canvas.clipPath(getPathA());
canvas.drawBitmap(mBitmapA, 0, 0, null);
canvas.restore();
}
/**
* 剪切C区域
*/
private void drawC(Canvas canvas) {
canvas.save();
canvas.clipPath(getPathA());
canvas.clipPath(getPathC(), Region.Op.REVERSE_DIFFERENCE);
canvas.drawBitmap(mBitmapC, 0, 0, null);
canvas.restore();
}
/**
* 剪切B区域
*/
private void drawB(Canvas canvas) {
canvas.save();
canvas.clipPath(getPathA());
canvas.clipPath(getPathC(), Region.Op.UNION);
canvas.clipPath(getPathB(), Region.Op.REVERSE_DIFFERENCE);
canvas.drawBitmap(mBitmapB, 0, 0, null);
canvas.restore();
}
/**
* 获取区域A的path
*/
private Path getPathA() {
mPathA.reset();
mPathA.lineTo(0, height);
mPathA.lineTo(c.x, c.y);
mPathA.quadTo(e.x, e.y, b.x, b.y);
mPathA.lineTo(a.x, a.y);
mPathA.lineTo(k.x, k.y);
mPathA.quadTo(h.x, h.y, j.x, j.y);
mPathA.lineTo(width, 0);
mPathA.close();
return mPathA;
}
/**
* 获取区域C的path
*/
private Path getPathC() {
mPathC.reset();
mPathC.moveTo(i.x, i.y);
mPathC.lineTo(d.x, d.y);
mPathC.lineTo(b.x, b.y);
mPathC.lineTo(a.x, a.y);
mPathC.lineTo(k.x, k.y);
mPathC.close();//闭合区域
return mPathC;
}
/**
* 获取区域B的path
*/
private Path getPathB() {
mPathB.reset();
mPathB.lineTo(0, height);
mPathB.lineTo(width, height);
mPathB.lineTo(width, 0);
mPathB.close();//闭合区域
return mPathB;
}
/**
* 计算各个点的坐标
*
* @param a a点的坐标
* @param f f点的坐标
*/
void calculationPoint(Point a, Point f) {
g.x = (a.x + f.x) / 2;
g.y = (a.y + f.y) / 2;
e.x = g.x - (f.y - g.y) * (f.y - g.y) / (f.x - g.x);
e.y = f.y;
h.x = f.x;
h.y = g.y - (f.x - g.x) * ((f.x - g.x) / (f.y - g.y));
c.x = e.x - (f.x - e.x) / 2;
c.y = f.y;
j.x = f.x;
j.y = h.y - (f.y - h.y) / 2;
b.x = (a.x + e.x) / 2;
b.y = (a.y + e.y) / 2;
k.x = (a.x + h.x) / 2;
k.y = (a.y + h.y) / 2;
d.x = ((c.x + b.x) / 2 + e.x) / 2;
d.y = ((c.y + b.y) / 2 + e.y) / 2;
i.x = ((k.x + j.x) / 2 + h.x) / 2;
i.y = ((k.y + j.y) / 2 + h.y) / 2;
}
}
2、限制翻页距离
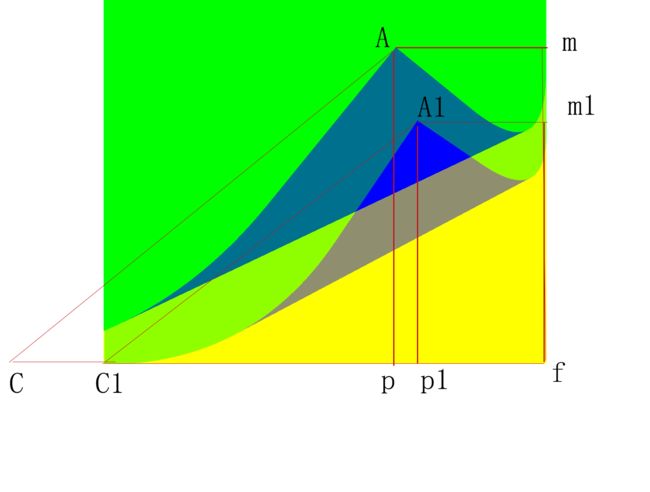
我们观察上面的翻页动画最后时,,我们的书籍随时翻动,但是左侧最后也随之翻动起来,这样明显不符合翻页的规则,我们对C点进行限制。
思考,若我们的C点为负数,即左侧也被翻起的时候,我们需要将C点一直放在零界点的位置,而j点继续向上移动,因此我们使用相似图形的原理,梯形camf和c1a1m1f1相似,重新计算a的坐标(a1)。
private void calculationAByYouch(){
float cf = width - c.x;
float pf = Math.abs(f.x - a.x);
float p1f = width * pf / cf;
a.x = Math.abs(f.x - p1f);
float h1 = Math.abs(f.y - a.y);
float a1p1 = h1 * pf / cf;
a.y = Math.abs(f.y - a1p1);
}
@Override
public boolean onTouchEvent(MotionEvent event) {
float x = event.getX();
float y = event.getY();
a.x = x;
a.y = y;
calculationPoint(a, f);
if (c.x<0){
calculationAByYouch();
calculationPoint(a, f);
}
postInvalidate();
return true;
}