官方网站 官方代码
第二章 排序
2.1 初级排序算法
排序就是将一组对象按照某种逻辑顺序重新排列的过程。这里我们主要关注重新排列含有元素的数组 (arrays of items)的算法,其中每个元素都有一个主键 (key)。排序算法的目的是重新排列所有元素,使得元素的主键能以某种方式排列。以下代码是本章通用的排序算法模板:
public class Example
{
public static void sort(Comparable[] a)
{ /*see text*/ }
private static boolean less(Comparable v, Comparable w)
{ return v.compareTo(w) < 0; }
private static void exch(Comparable[] a, int i, int j)
{ Comparable t = a[i]; a[i] = a[j]; a[j] = t; }
private static void show(Comparable[] a)
{
for (int i = 0; i < a.length; i++)
StdOut.print(a[i] + " ");
StdOut.println();
}
public static boolean isSorted(Comparable[] a)
{
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
public static void main(String[] args)
{
String[] a = In.readStrings();
sort(a);
assert isSorted(a);
show(a);
}
}- 排序成本模型:在研究排序算法时,需要计算比较(compares) 和 交换(exchanges)的数量。对于不交换元素的算法,则计算访问数组 (array accesses)的次数。
- 排序算法可分为两类:一种是无需额外内存的就地排序算法;一种是需要额外内存空间来存储另一份数组副本的排序算法。
Comparable接口
此接口强行对实现它的每个类的对象进行整体排序。Java中的封装数字的类型Integer和Double,以及String和其他许多高级数据类型都实现了Comparable接口,因此可以直接用这些类型的数组作为参数调用排序算法,如下图快速排序调用数组a:
在创建自己的数据类型时,只要实现Comparable接口就能保证用例代码可以将其排序。要做到这一点,需要实现一个compareTo ()方法来定义目标类型对象的自然次序 。如下图的Date数据类型:
compareTo() 方法 实现了对主键 (key) 的抽象 —— 对于任何实现了Comparable接口的数据类型,该方法定义了对象的大小顺序。
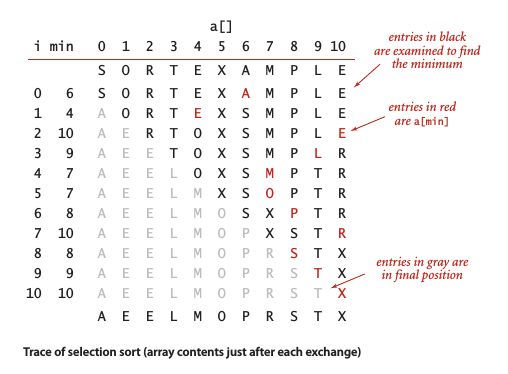
选择排序 (Selection Sort)
public class Selection
{
public static void sort(Comparable[] a)
{
int N = a.length;
for (i = 0; i < N; i++)
{
int min = i;
for (j = i+1; j < N; j++)
if (less(a[j], a[min])) min = j;
exch(a, i, min);
}
}
}对于长度为N的数组,选择排序需要大约 \(~N^2/2\)次比较和N次交换。
选择排序的特点:
- 运行时间和输入无关:一个以及排好序的数组或主键全部相等的数组和一个随机排列的数组所用的排序时间相同。
- 数据移动是最少的:总共N次交换,交换次数和数组大小是线性关系,其他排序算法都不具备这个特征 (大多为线性对数或平方级别)。
插入排序 (Insert Sort)
public class Insertion
{
public static void sort(Comparable[] a)
{
int N = a.length;
for (int i = 1; i < N; i++)
{
for (int j = i; j > 0 && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
}
}
和选择排序不同,插入排序所需的时间取决于输入元素的初始顺序,对一个很大且其中元素已经有序 (或接近有序) 的数组进行排序要比对随机数组或逆序数组进行排序要快得多。
提高插入排序速度的方式:在内循环中将较大的元素向右移动而不总是交换两个元素(这样访问数组的次数就能减半)。
public class InsertionX
{
public static void sort(Comparable[] a)
{
int N = a.length;
for (int i = 1; i < N; i++)
{
Comparable temp = a[i];
for (j = i; j > 0 && less(temp, a[j-1]); j--)
a[j] = a[j-1];
}
a[j] = temp;
}
}
// alternative way
public class InsertionX
{
public static void sort(Comparable[] a)
{
int N = a.length;
for (int i = 1; i < N; i++)
{
Comparable temp = a[i];
int j = i;
while (j > 0 && less(temp, a[j-1]))
{
a[j] = a[j-1];
j--;
}
a[j] = temp;
}
}
}排序算法的比较
public class SortCompare
{
public static double time(String alg, Comparable[] a)
{
Stopwatch timer = new Stopwatch();
if (alg.equals("Insertion")) Insertion.sort(a);
if (alg.equals("Selection")) Selection.sort(a);
if (alg.equals("Shell")) Shell.sort(a);
if (alg.equals("Merge")) Merge.sort(a);
if (alg.equals("Quick")) Quick.sort(a);
if (alg.equals("Heap")) Heap.sort(a);
return timer.elapsedTime();
}
public static double timeRandomInput(String alg, int N, int T)
{
double total = 0.0;
Double[] a = new Double[N];
for (int t = 0; t < T; t++)
{
for (int i = 0; i < N; i++)
a[i] = StdRandom.uniform();
total += time(alg, a);
}
return total;
}
public static void main(String[] args)
{
String alg1 = args[0];
String alg2 = args[1];
int N = Integer.parseInt(args[2]);
int T = Integer.parseInt(args[3]);
double t1 = timeRandomInput(alg1, N, T);
double t2 = timeRandomInput(alg2, N, T);
StdOut.printf("For %d random Doubles\n %s is", N, alg1);
StdOut.printf(" %.1f times faster than %s\n", t2/t1, alg2);
}
}
/**********************************************
% java SortCompare Insertion Selection 1000 100
For 1000 random Doubles
Insertion is 1.7 times faster than Selection
**********************************************/希尔排序 (Shell Sort)
希尔排序是插入排序的改进,插入排序的缺点是每次只能交换相邻的元素,若主键最小的元素恰好在数组的末尾,则需要N-1次移动。希尔排序的思想是通过交换不相邻的元素使数组中任意间隔为h的元素都是有序的,并最终用插入排序将局部有序的数组排序。
public class Shell
{
public static void sort(Comparable[] a)
{
int N = a.length;
int h = 1;
while (h < N/3) h = 3*h + 1;
while (h >= 1)
{
for (int i = h; i < N; i++)
{
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h)
exch(a, j, j-h)
}
h = h/3;
}
}
}
/********************************************
% java SortCompare Shell Insertion 100000 100
For 100000 random Doubles
Shell is 600 times faster than Insertion
*********************************************/
2.2 归并排序 (Mergesort)
归并排序一般是 (递归地) 将数组分成两半分别排序,然后将结果归并起来。归并排序的优点是所需的时间和 \(NlgN\) 成正比,这使得其优于选择排序和插入排序。缺点是辅助数组所需的额外空间与N的大小成正比。归并排序是分治 (divide-and-conquer) 思想的典型体现。
自上而下的归并排序
public class Merge
{
private static Comparable[] aux;
public static void sort(Comparable[] a)
{
aux = new Comparable[a.length];
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, lo, mid);
sort(a, mid+1, hi);
merge(a, lo, mid, hi);
}
public static boid merge(Comparable[] a, int lo, int mid, int hi)
{
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++)
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
private static boolean less(Comparable v, Comparable w)
{ return v.compareTo(w) < 0; }
}自下而上的归并排序
public class MergeBU
{
private static Comparable[] aux;
public static void sort(Comparable[] a)
{
int N = a.length;
aux = new Cmparable[N];
for ( int sz = 1; sz < N; sz = sz+sz)
for (int lo = 0; lo < N-sz; lo += sz+sz)
merge(a, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
}
public staic boid merge(Comparable[] a, int lo, int mid, int hi)
{
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++)
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
private static boolean less(Comparable v, Comparable w)
{ return v.compareTo(w) < 0; }
}2.3 快速排序 (Quicksort)
在一般应用中快速排序都比其他排序算法快得多,除此之外快速排序是原地排序,所需时间和 \(NlgN\)成正比。主要缺点是非常脆弱,在实现时需要非常小心才能避免低劣的性能。
快速排序也是一种分治的排序算法。与归并排序的区别:归并排序将两个子数组分别排序后,归并前整个数组不是有序的;快速排序则是当子数组都有序时整个数组也就自然有序了。在归并排序中,一个数组被分成两半;快速排序中,切分 (partition) 的位置取决于数组的内容。
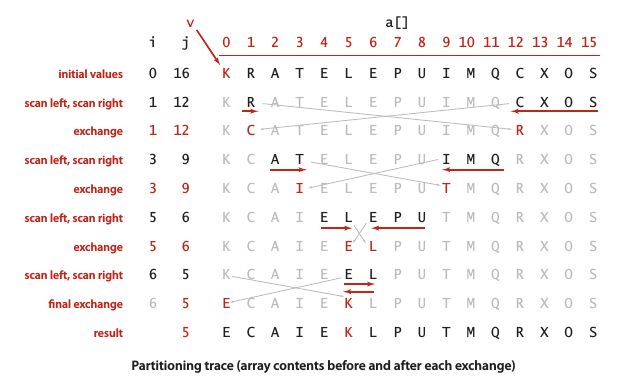
快速排序递归地将子数组 a[lo...hi] 排序,先用partition()方法将a[j] 放到一个合适位置,然后递归地将其他位置的元素排序。这里的关键在于切分,切分后数组满足三个条件:
- 对于某个j,a[j] 在其最终位置
- a[lo] 到 a[j-1] 的所有元素都不大于 a[j]
- a[j+1] 到 a[hi] 的所有元素都不小于 a[j]

切分的实现方法:先取a[lo] 作为切分元素,然后从数组左端开始向右扫描直到找到一个大于等于它的元素,再从右端开始向左扫描知道找到一个小于等于它的元素,最后交换这两个元素的位置。当两个指针相遇时,将切分元素a[lo] 和左子数组最右侧的元素 (a[j]) 交换,这样切分值就留在a[j]中。
public class Quick
{
public static void sort(Comparable[] a)
{
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
private static int partition(Comparable[] a, int lo, int hi)
{
int i = lo, j = hi + 1;
Comparable v = a[lo];
while (true)
{
while (less(a[++i], v)) if (i == hi) break;
while (less(v, a[--j])) if (j == lo) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
}上述快速排序的实现有一个潜在的缺点:在切分不平衡时可能会极为低效,达到平方级别。例如如果从最小的元素切分,第二次从第二小的元素切分,如此这般每次只移除一个元素,这会导致一个大数组需要切分很多次。因此快速排序前需要现将数组随机排序。
切换到插入排序: 对于小数组,快速排序比插入排序慢,所以可将上述算法中sort() 方法从
if (hi <= lo) return;改为if (hi <= lo + M) { Insertion.sort(a, lo, hi); return; }
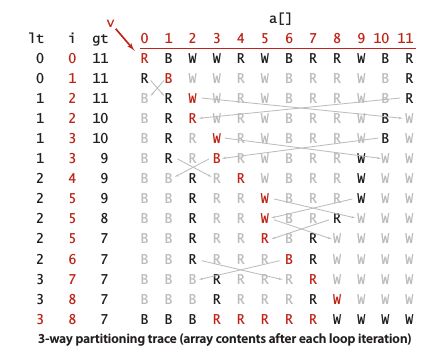
三向切分排序
当数组中存在大量重复元素时,快速排序的效率可以通过三向切分排序进一步改进,能将排序时间从线性对数级下降到线性级别。将数组分为三部分,分别对应小于、等于和大于切分元素的数组元素。使用Comparable 接口对a[i] 进行三向比较:
- a[i] 小于v,将a[lt] 和 a[i] 交换,将 lt 和 i 加一
- a[i] 大于v,将 a[gt] 和 a[i] 交换,将 gt 减一
- a[i] 等于v,将 i 加一
public class Quick3way
{
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int lt = lo, i = lo + 1, gt = hi;
Comparable v = a[lo];
while (i <= gt)
{
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
}2.4 优先队列 (Prior Queues)
普通的队列 (queue) 是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。这种队列不是直接将新元素放在队列尾部,而是放在比它优先级低的元素前面。
优先队列最重要的操作是删除最大元素 (delMax()) 和插入元素 (insert()) ,见以下API:
以下是一个优先队列的测试用例,打印数字最大的M行:
public class TopM
{
public static void main(String[] args)
{
int M = Integer.parseInt(args[0]);
MinPQ pq = new MinPQ(M+1);
while (StdIn.hasNextLine())
{
pq.insert(new Transaction(StdIn.readLine()));
if (pq.size() > M)
pd.delMin();
}
Stack stack = new Stack();
while (!pq.isEmpty()) stack.push(pq.delMin());
for (Transaction t : stack) StdOut.println(t);
}
} 堆的定义
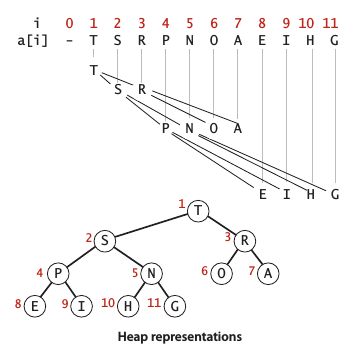
数据结构二叉堆 (binary heap) 能很好地实现优先队列的基本操作。二叉堆是一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级存储 (不使用数组的第一个位置)。堆有序 (heap-ordered) 指的是一颗二叉树的每个结点都大于等于它的两个子结点。
在一个堆中,位置为k的结点的父结点位置为\(\left\lfloor k/2 \right\rfloor\) ,两个子结点的位置分别为 \(2k\) 和 \(2k+1\)。一颗大小为N的完全二叉树的高度为\(\left\lfloor lgN \right\rfloor\)
堆的算法
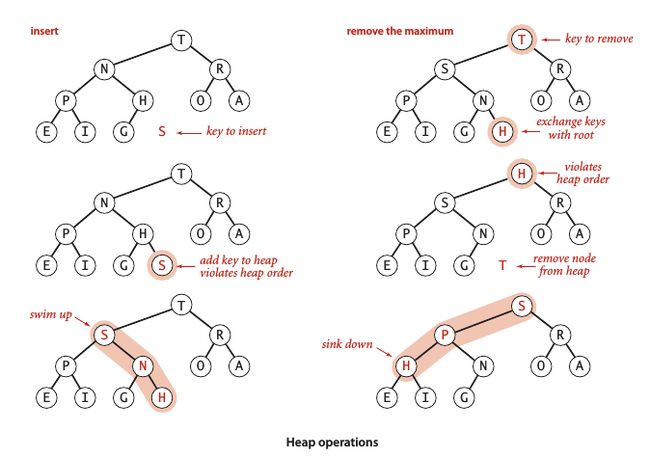
自下而上的堆有序化 —— 上浮 (swim)
如果某个结点比其父结点大,则需要交换二者以保持堆的有序化,这样的循环过程为swim() 方法: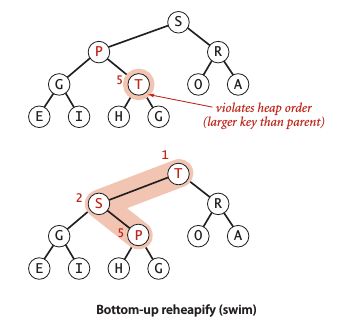
private void swim(int k)
{
while (k > 1 && less(k/2, k))
{
exch(k/2, k);
k = k/2;
}
}自上而下的堆有序化 —— 下沉 (sink)
如果某个结点比其两个子结点的其中之一小,则需要将它和两个子结点的较大者交换以保持堆的有序化这样的循环过程为sink() 方法:
private void sink(int k)
{
while (2*k <= N)
{
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}插入元素:将新元素加到数组末尾,增加堆的大小并将这个元素上浮到合适位置。
删除最大元素:从数组顶端删去最大元素并将数组最后一个元素放到顶端,再让这个元素下沉到合适位置。
下列代码实现了优先队列,优先队列由一个基于堆的完全二叉树表示,存储于数组 pq[1...N] 中,pq[0] 没有使用。
public class MaxPQ>
{
private Key[] pq;
private int N = 0;
public MaxPQ(int maxN)
{ pq = (Key[]) new Comparable[maxN+1]; }
public boolean isEmpty()
{ return N == 0; }
public int size()
{ return N; }
public void insert(Key v)
{
pq[++N] = v;
swim(N);
}
public Key delMax()
{
Key max = pq[1];
exch(1, N--);
pq[N+1] = null;
sink(1);
return max;
}
private boolean less(int i, int j)
{ return pq[i].compareTo(pq[j]) < 0; }
private void exch(int i, int j)
{ Key t = pq[i]; pq[i] = pq[j]; pq[j] = t; }
private void swim(int k)
{
while (k > 1 && less(k/2, k))
{
exch(k/2, k);
k = k/2;
}
}
private void sink(int k)
{
while (2*k <= N)
{
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
} 索引优先队列 (Index Priority Queue)
索引优先队列即在优先队列的基础上给数组中每个元素添加一个索引。以下实现用pq[]保存索引,qp[]保存pq[]的逆序,即pq[]中元素的位置。举例:pq = [1,2,0], 则qp = [2,0,1],pq[qp[1]]=1 。数组keys[]保存元素。
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.In;
public class IndexMinPQ>
{
private int maxN;
private int n;
private int[] pq;
private int[] qp;
private Key[] keys;
public IndexMinPQ(int maxN)
{
this.maxN = maxN;
n = 0;
keys = (Key[]) new Comparable[maxN + 1];
pq = new int[maxN + 1];
qp = new int[maxN + 1];
for (int i = 0; i <= maxN; i++)
qp[i] = -1;
}
public boolean isEmpty()
{ return n == 0; }
public boolean contains(int i)
{ return qp[i] != -1; }
public int size()
{ return n; }
public void insert(int i, Key key)
{
n++;
qp[i] = n;
pq[n] = i;
keys[i] = key;
swim(n);
}
public int minIndex()
{ return pq[1]; }
public Key minKey()
{ return keys[pq[1]]; }
public int delMin()
{
int min = pq[1];
exch(1, n--);
sink(1);
assert min == pq[n+1];
qp[min] = -1;
keys[min] = null;
pq[n+1] = -1;
return min;
}
public void changeKey(int i, Key key)
{
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
public void delete(int i)
{
int index = qp[i];
exch(index, n--);
swim(index);
sink(index);
keys[i] = null;
qp[i] = -1;
}
private boolean greater(int i, int j)
{ return keys[pq[i]].compareTo(keys[pq[j]]) > 0; }
private void exch(int i, int j)
{
int swap = pq[i];
pq[i] = pq[j];
pq[j] = swap;
qp[pq[i]] = i;
qp[pq[j]] = j;
}
private void swim(int k)
{
while (k > 1 && greater(k/2, k))
{
exch(k, k/2);
k = k/2;
}
}
private void sink(int k)
{
while (2*k <= n)
{
int j = 2*k;
if (j < n && greater(j, j+1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
/******************************************************
以下为用例:多向归并问题,将多个有序的输入流归并成一个有序的输出流
******************************************************/
public static void merge(In[] streams)
{
int N = streams.length;
IndexMinPQ pq = new IndexMinPQ(N);
for (int i = 0; i < N; i++)
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
while (!pq.isEmpty())
{
StdOut.printf(pq.minKey() + " ");
int i = pq.delMin();
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
}
}
public static void main(String[] args)
{
int N = args.length;
In[] streams = new In[N];
for (int i = 0; i < N; i++)
streams[i] = new In(args[i]);
merge(streams);
StdOut.println();
}
}
/*************
输入:
% more m1.txt
A B C F G I I Z
% more m2.txt
B D H P Q Q
% more m3.txt
A B E F J
输出:
% java IndexMinPQ m1.txt m2.txt m3.txt
A A B B B C D E F F G H I I J N P Q Q Z
**************************************/ 堆排序 (Heapsort)
堆排序可分为两个阶段:
- 堆的构造:将原始数组重新组织安排进一个堆中
- 下沉 (sink) 排序:从堆中按递减顺序取出所有元素并得到排序结果
堆的构造通过从下到上递归地构建子堆来实现。如果一个结点的两个子结点都已经是堆了,那么在该结点上调用sink() 就能把它们变成一个堆,这样就能按数组逆序从下而上地构建堆。只需对数组中一半元素使用 sink()方法,因为剩下的元素都是叶结点。完成后堆的最大元素将位于数组的开头。
下沉排序阶段将顶端和末端元素进行交换,然后将最大元素从堆中删除并用 sink() 重新调整堆的结构,如此循环最后得到一个有序序列。
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class Heap
{
private Heap() { }
public static void sort(Comparable[] pq)
{
int n = pq.length;
for (int k = n/2; k >= 1; k--)
sink(pq, k, n);
while (n > 1)
{
exch(pq, 1, n--);
sink(pq, 1, n);
}
}
private static void sink(Comparable[] pq, int k, int n)
{
while (2*k <= n)
{
int j = 2*k;
if (j < n && less(pq, j, j+1)) j++;
if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
}
private static boolean less(Comparable[] pq, int i, int j)
{ return pq[i-1].compareTo(pq[j-1]) < 0; }
private static void exch(Object[] pq, int i, int j)
{
Object swap = pq[i-1];
pq[i-1] = pq[j-1];
pq[j-1] = swap;
}
private static void show(Comparable[] a)
{
for (int i = 0; i < a.length; i++)
StdOut.println(a[i]);
}
public static void main(String[] args)
{
String[] a = StdIn.readAllStrings();
Heap.sort(a);
show(a);
}
}2.5 应用
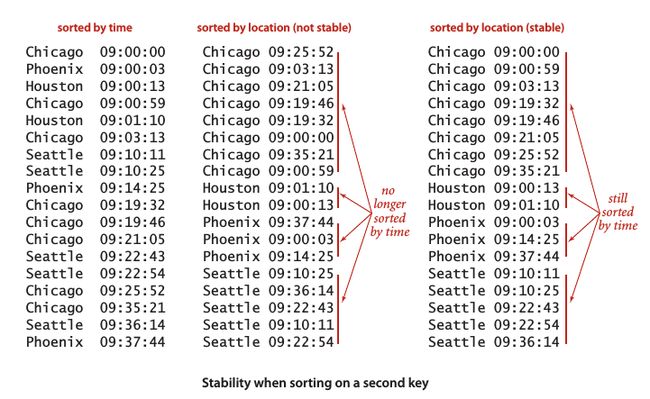
- 排序算法的稳定性:如果一个排序算法能够保留数组中重复元素的相对位置则可以被称为是稳定的。
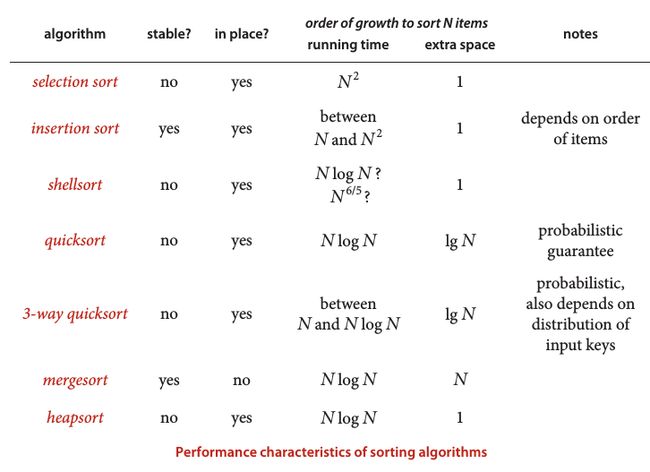
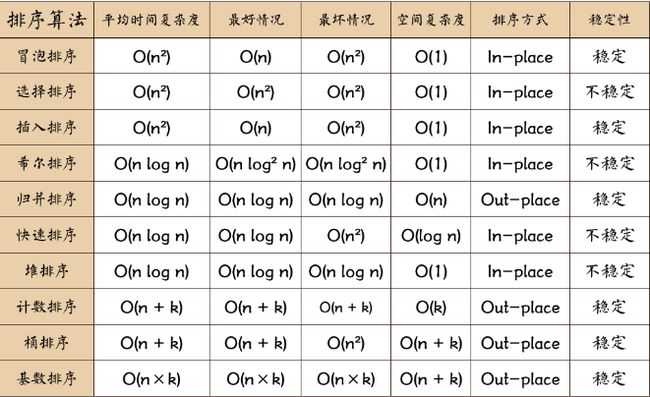
排序算法的比较
找出重复元素
只需线性对数的时间,先将数组排序,再遍历数组,记录连续出现的重复元素。如果用平方级别的算法则要将所有元素相互比较一遍。
Quick.sort(a);
int count = 1;
for (int i = 1; i < a.length; i++)
if (a[i].compareTo(a[i-1]) != 0)
count++;
/