本文主要作为自己的学习笔记,并不具备过多的指导意义。
目录
- 基本概念
- 二叉树的重点
- 二叉树的遍历
- 实现先序遍历
- 实现中序遍历
- 实现后序遍历
- 以每层换行的方式进行广度遍历
- 二叉树的序列化和反序列化
- 前序遍历的归档&&解归档
- 广度遍历归档&&解归档
- 二叉树的子树
- 平衡二叉树(AVL树)
- 搜索二叉树
- 满二叉树
- 完全二叉树
- 后序节点与前驱节点
- 二叉树中两节点间的距离
- 参考资料
基本概念
-
基本结构
本节点的值,左子节点,右子节点。(以及一个初始化赋值)
public class TreeNode {
public var val: Int
public var left: TreeNode?
public var right: TreeNode?
public init(_val: Int) {
self.val = val
}
}
二叉树的重点
-
能够结合队列,栈,链表,字符串等很多数据结构出题。
-
基本遍历方式:比如BFS(广度),DFS(深度)。
-
递归的使用
二叉树的遍历
先序,中序,后序遍历为最常见的树的三种遍历方式。这三种写法相似,无非是递归的顺序略有不同。
-
先序遍历
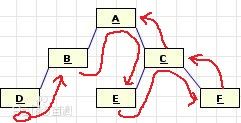
先序遍历先从二叉树的根开始,然后到左子树,再到右子树。
遍历的结果是:ABDCEF
-
中序遍历
中序遍历先从左子树开始,然后到根,再到右子树。
遍历的结果是:DBAECF
-
后续遍历
后序遍历先从左子树开始,然后到右子树,再到根。
遍历的结果是:DBEFCA
实现先序遍历
-
递归
打印自己,然后先遍历左节点再遍历右节点
/// 先序遍历--递归
///
/// - Parameter node: 遍历节点
func preorderRecur(node: TreeNode?) {
if node == nil {
return
}
print(node!.val)//打印当前节点
preorderRecur(node: node!.left)//遍历左节点
preorderRecur(node: node!.right)//遍历右节点
}
-
非递归
先尝试将左元素入栈,若栈顶元素为空则将栈顶推出然后尝试遍历右节点。直到栈为空则遍历结束。
这里的栈用处是为了保存二叉树的结构,以弥补二叉树无法获取父节点的结构特性。
/// 先序遍历--while
///
/// - Parameter root: 根节点
/// - Returns: 遍历结果数组
func preorderTraversals(root: TreeNode?) -> [Int] {
var res = [Int]()
var stack = [TreeNode]() //遍历用的栈
var node = root//遍历的根节点
while !stack.isEmpty || node != nil {
if node != nil {
res.append(node!.val) //将当前节点的值记录
stack.append(node!) //将当前节点加入栈中
node = node!.left //尝试遍历当前节点的左节点
} else {
let parentsNode = stack.removeLast() //取出当前节点的父节点
node = parentsNode.right //将栈顶节点推出,并尝试遍历其父元素的右节点。
}
}
return res
}
-
还有一种方式
这种方式纯粹的利用栈的性质,每次弹出栈顶元素,并尝试将其左右孩子入栈。
不过需要注意的是后入栈的为左孩子,以保证优先遍历左侧。
func preorderTraversal(root: TreeNode?) -> [Int] {
var res = [Int]()
var stack = [TreeNode]() //遍历用的栈
var node = root//遍历的根节点
stack.append(root!)
while !stack.isEmpty{
res.append(stack.last!.val)
node = stack.removeLast()
if node!.right != nil {
stack.append(node!.right!)
}
if node!.left != nil {
stack.append(node!.left!)
}
}
return res
}
实现中序遍历
-
递归
/// 中序遍历--递归
///
/// - Parameter node: 遍历节点
func inorderRecur(node: TreeNode?) {
if node == nil {
return
}
inorderRecur(node: node!.left)//遍历左节
print(node!.val)//打印当前节点
inorderRecur(node: node!.right)//遍历右节点
}
-
非递归
与前序遍历相同,只是记录的时间不一样了
func inorderTraversal(root: TreeNode?) -> [Int] {
var res = [Int]()
var stack = [TreeNode]()
var node = root
while !stack.isEmpty || node != nil {
if node != nil {
stack.append(node!) //将当前节点依次入栈
node = node!.left //尝试遍历左节点
} else {
let parentsNode = stack.removeLast() //取出当前节点的父节点
res.append(parentsNode.val) //打印父节点
node = parentsNode.right //尝试遍历右节点
}
}
return res
}
-
先序遍历与中序遍历的非递归实现都是尝试分解左边界的过程
实现后序遍历
-
递归
/// 后序遍历--递归
///
/// - Parameter node: 遍历节点
func posorderRecur(node: TreeNode?) {
if node == nil {
return
}
posorderRecur(node: node!.left)//尝试遍历左节
posorderRecur(node: node!.right)//尝试遍历右节点
print(node!.val)//打印当前节点
}
-
非递归
用两个栈来实现。
第一个栈的处理顺序为,自上而下,自右而左。经过第二个栈的逆序,就变成了自下而上,自左而右。
-
另一种非递归
与之前两种遍历方式不同,我们需要引入一个新的变量
lastPrint来记录最后一次打印的节点。以此判断左,右节点是否已经被打印。
func posorderTraversal(root: TreeNode?) -> [Int] {
if root == nil {
return []
}
var res = [Int]()
var stack = [TreeNode]()
var node = root
var lastPrint : TreeNode? //最后一次打印的节点
stack.append(node!)
while !stack.isEmpty{
node = stack.last
if node?.left != nil && node?.left != lastPrint && node?.right != lastPrint{
stack.append((node?.left)!) //node的左子树一定没有打印完毕
}else if node?.right != nil && node?.right != lastPrint {
stack.append((node?.right)!) //node的右子树一定没有打印完毕
}else {
//node的左右子树全部打印完毕,寻找其父节点
res.append(stack.last!.val)
lastPrint = stack.removeLast()
}
}
return res
}
以每层换行的方式进行广度遍历
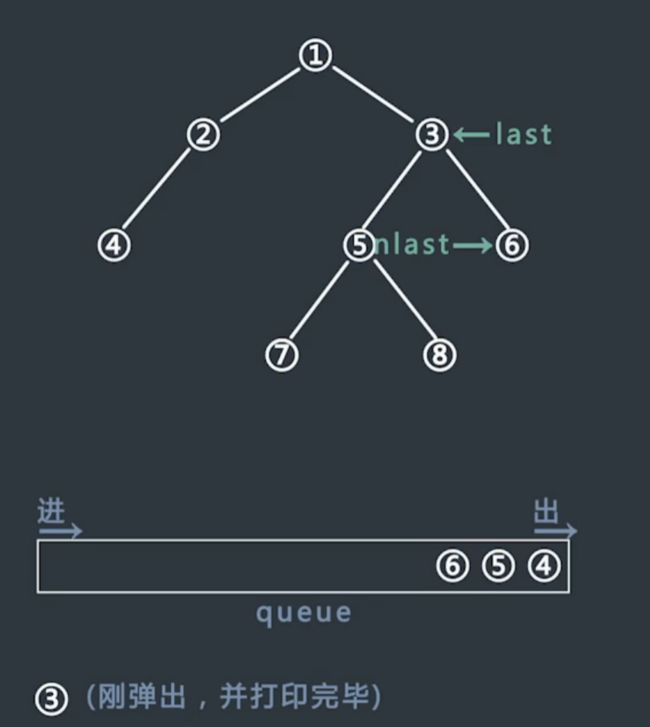
层数变换的记录,需要两个变量。
当前行最右节点(last)以及下一行最右(nlast)。
-
具体操作上
每次将新节点加入队列时,将nlast更新成新节点。
当当前打印的节点等于last,执行换行并将last更新到下一行nlast。
-
代码实现
func BFSTraversal(root: TreeNode?) -> String {
if root == nil {
return ""
}
var res = ""
var queue = [TreeNode]()
var last = root
var nlast = root
queue.append(root!)
while !queue.isEmpty {
let node = queue.removeFirst() //将队首节点出队
res += node.val.description + " " //打印队首节点
if node.left != nil { //尝试将左节点入队
queue.append(node.left!)
nlast = node.left!
}
if node.right != nil { //尝试将右节点入队
queue.append(node.right!)
nlast = node.right!
}
if node == last { //换行
last = nlast
res += "\n"
}
}
return res
}
二叉树的序列化和反序列化
-
序列化方式
- 先序遍历序列化
- 中序遍历序列化
- 后序遍历序列化
- 按层遍历序列化
-
一棵树序列化的结果和反序列化生成的二叉树都是唯一的
-
序列化和遍历二叉树的区别
- 序列化时需要转化成字符串,所以每个节点之间需要用符号进行分割
- 序列化时需要记录空节点,需要特殊符号进行记录
举个例子(用!分割,用#表空):
//序列化
5!12!20!#!#!22!#!#!17!21!#!#!23!#!33!40!#!#!
//遍历
[5, 12, 20, 22, 17, 21, 23, 33, 40]
-
反序列化
将序列化字符串转化成数组(比如这里通过!分割)
//字符串
5!12!20!#!#!22!#!#!17!21!#!#!23!#!33!40!#!#!
//数组
["5", "12", "20", "#", "#", "22", "#", "#", "17", "21", "#", "#", "23", "#", "33", "40", "#", "#"]
前序遍历的归档&&解归档
-
归档
/// 先序遍历归档--递归
///
/// - Parameter node: 遍历节点
func preorderRecurArchive(node: TreeNode?) -> String {
if node == nil {
return "#!"
}
var res = (node?.val.description)! + "!"
res += preorderRecurArchive(node: node!.left)//遍历左节点
res += preorderRecurArchive(node: node!.right)//遍历右节点
return res
}
/// 先序遍历格式化--while
///
/// - Parameter root: 根节点
/// - Returns: 序列化字符串
func preorderArchive(root: TreeNode?) -> String {
var res = ""
var stack = [TreeNode]() //遍历用的栈
var node = root//遍历的根节点
while !stack.isEmpty || node != nil {
if node != nil {
res += node!.val.description + "!" //将当前节点的值记录
stack.append(node!) //将当前节点加入栈中
node = node!.left //尝试遍历当前节点的左节点
} else {
let parentsNode = stack.removeLast() //取出当前节点的父节点
node = parentsNode.right //将栈顶节点推出,并尝试遍历其父元素的右节点。
res += "#!" //记录空节点
}
}
res += "#!" //记录空节点
return res
}
-
解归档
递归
/// 前序遍历解归档--递归
///
/// - Parameter str: 归档字符串
/// - Returns: 头节点
func preorderRecurRearchive(str: String?) -> TreeNode? {
var treeQueue = (str?.components(separatedBy: "!"))!
treeQueue.removeLast() //这里切割完毕之后最后数组的最后一位为""
return preorderRecurRearchiveProcess(treeQueue: &treeQueue)
}
/// 根据前序队列进行二叉树重构
///
/// - Parameter treeQueue: 节点队列
/// - Returns: 头节点
func preorderRecurRearchiveProcess(treeQueue : inout [String]) -> TreeNode? {
let value = treeQueue.removeFirst()
if value == "#" { //头节点为空
return nil
}
let root = TreeNode.init(_val: Int(value)!) //设置根节点
root.left = preorderRecurRearchiveProcess(treeQueue: &treeQueue) //设置左节点
root.right = preorderRecurRearchiveProcess(treeQueue: &treeQueue) //设置右节点
return root
}
非递归
与遍历时不同,我们无法通过节点是否为nil判断该构建哪一个子节点。
所以我们需要引入一个变量setleft来确定下一次需要构建的节点方向。
需要注意的是:
每次构建新节点之后,下一次都会尝试构建其左侧节点。
而每次遇到空节点后,都会将顶元素推出,并尝试构建其的右侧节点。
/// 前序遍历解归档
///
/// - Parameter str: 归档字符串
/// - Returns: 头节点
func preorderRearchive(str: String?) -> TreeNode? {
var treeQueue = (str?.components(separatedBy: "!"))!
treeQueue.removeLast() //这里切割完毕之后最后数组的最后一位为""
var stack = [TreeNode]() //遍历用的栈
var node : TreeNode //当前操作的节点
if treeQueue.isEmpty || treeQueue.first == "#" { //头节点为空
return nil
}
let root = TreeNode.init(_val: Int(treeQueue.removeFirst())!) //设置root节点
node = root//将头节点记录为当前操作的节点
stack.append(root) //将头节点记录
var setleft = true //记录当前需要构建的节点方向
while !treeQueue.isEmpty {
let value = treeQueue.removeFirst() //将队列首元素推出
if value != "#" { //若当前节点不为空
let newNode = TreeNode.init(_val: Int(value)!) //获得新的节点
//与当前节点相连
if setleft {
node.left = newNode
}else {
node.right = newNode
}
node = newNode //记录当前节点
stack.append(node) //记录当前层级
setleft = true //下一次,尝试构建左节点
}else {
if treeQueue.isEmpty {
return root //如果已经遍历完成
}else {
node = stack.removeLast() //尝试构建上层
}
setleft = false //下一次,尝试构建右节点
}
}
return root //返回头节点
}
广度遍历归档&&解归档
广度遍历的归档&&解归档比深度遍历容易理解的多。
因为他的队列,只负责记录下一次想要处理的节点。
并不需要在意左右与层级倒退,只需要处理节点为空的情况即可。
-
归档
/// 广度遍历归档
///
/// - Parameter root: 头节点
/// - Returns: 归档字符串
func BFSArchive(root: TreeNode?) -> String {
if root == nil {
return ""
}
var res = ""
var queue = [TreeNode]()
queue.append(root!)
res += root!.val.description + "!"
while !queue.isEmpty {
let node = queue.removeFirst() //将当前节点出队
if node.left != nil { //尝试将左节点入队
queue.append(node.left!)
res += node.left!.val.description + "!" //打印当前节点
}else {
res += "#!" //打印当前节点
}
if node.right != nil { //尝试将右节点入队
queue.append(node.right!)
res += node.right!.val.description + "!" //打印当前节点
}else {
res += "#!" //打印当前节点
}
}
return res
}
-
解归档
/// 广度遍历解归档
///
/// - Parameter str: 归档字符串
/// - Returns: 头节点
func BFSRearchive(str: String?) -> TreeNode?{
var treeQueue = (str?.components(separatedBy: "!"))!
var i = 0
treeQueue.removeLast() //这里切割完毕之后最后数组的最后一位为""
var queue = [TreeNode]()
if treeQueue.isEmpty || treeQueue.first == "#" { //头节点为空
return nil
}
let root = TreeNode.init(_val: Int(treeQueue[i])!) //设置root节点
i+=1
queue.append(root)
while !queue.isEmpty && i二叉树的子树
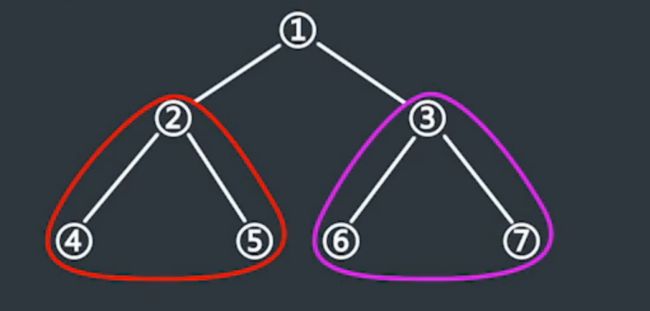
在二叉树中以任何一个节点为头部,其下方的整棵树作为二叉树的子树。
-
子树
-
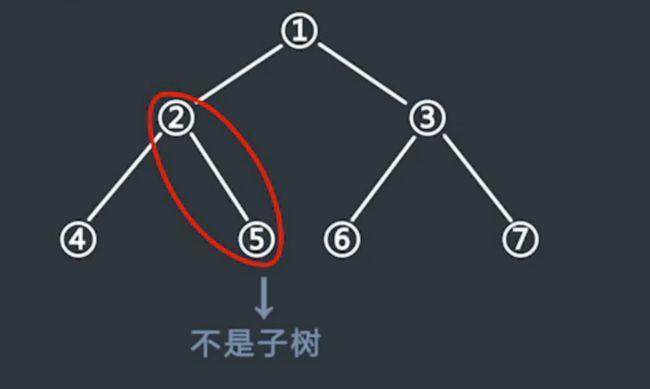
非子树
平衡二叉树(AVL树)
- 空树为平衡二叉树
- 不为空的二叉树。其中所有的子树,左右两侧高度差不超过1。
如下图中第三棵二叉树。
2节点的子树下方,左侧高度为2,右侧高度为0。所以不是一个平衡二叉树。
-
判断是否为平衡二叉树
通过递归的方式判断每个子树是否为AVL树
一旦一侧子节点为空,另一侧若高度大于2,则判定为否
/// 是否为平衡二叉树
///
/// - Parameter root: 子树头节点
/// - Returns: 子树是否平衡
func isBalance(root : TreeNode?) -> Bool {
if root == nil { //空树为AVL树
return true
}
let left = root?.left
let right = root?.right
if ((left?.left != nil) || (left?.right != nil)) && right == nil{
return false //左侧比右侧高2
}
if ((right?.left != nil) || (right?.right != nil)) && left == nil{
return false //右侧比左侧高2
}
//否则继续判定子树
if isBalance(root: left) && isBalance(root: right) {
return true
}else {
return false
}
}
搜索二叉树
又叫二叉查找树,二叉排序树
特征为,每个子树的头节点>左节点,并且头节点<右节点
二叉树的中序排列,一定是一个有序数组。反之亦然
红黑树,平衡搜索二叉树(平衡AVL树)等,都是搜索二叉树的不同实现。
目的都是提高搜索二叉树的效率,调整代价降低。
-
判断一个二叉树是否为搜索二叉树
在中序遍历中,如果上次的值小于当前的值,则证否
/// 判断一个二叉树树否为搜索二叉树
///
/// - Parameter root: 根节点
/// - Returns: 结果
func isBST(root: TreeNode?) -> Bool {
var stack = [TreeNode]()
var node = root
var lastValue = -NSIntegerMax
while !stack.isEmpty || node != nil {
if node != nil {
stack.append(node!) //将当前节点依次入栈
node = node!.left //尝试遍历左节点
} else {
let parentsNode = stack.removeLast() //取出当前节点的父节点
if lastValue > parentsNode.val {
return false
}
lastValue = parentsNode.val
node = parentsNode.right //尝试遍历右节点
}
}
return true
}
-
复原一个交换了位置的搜索二叉树
搜索二叉树本身的中序遍历是升序排序。一旦有两节点交换了位置,就一定有一到两个部分产生降序。
#1. 遍历中出现了两次局部降序
#1,2,3,4,5
#1,5,3,4,2
第一个错误的节点为第一次降序较大的节点
第二个错误的节点为第二次降序较小的节点
#2. 遍历中只出现了一次局部降序
#1,2,3,4,5
#1,2,4,3,5
第一个错误的节点为此次降序较大的节点
第二个错误的节点为此次降序较小的节点
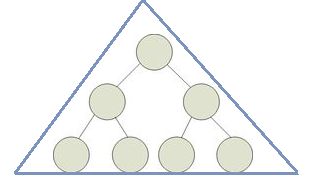
满二叉树
-
对于国内的满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
从图形形态上看,满二叉树外观上是一个三角形
国内的满二叉树属于完全二叉树
这种满二叉树的层数为L,节点数为N。
则N = 2^L-1 ,L = log(N+1)
-
对于国外的满二叉树
满二叉树的结点要么是叶子结点,度为0,要么是度为2的结点,不存在度为1的结点。
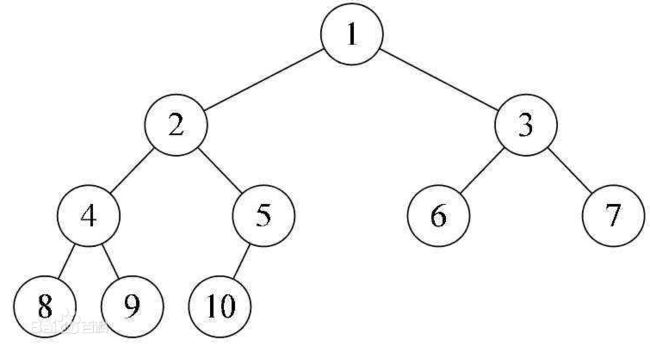
完全二叉树
在满二叉树的基础上,最后一层所有的结点都连续集中在最左边,这就是完全二叉树。
-
判断完全二叉树
通过宽度遍历的方式进行。
-
计算完全二叉树的节点个数,要求复杂度小于O(N)
完全二叉树的左右子树,一定有一边是满二叉树(左侧高度H,右侧高度H-1)。
先遍历左子树左边界,再遍历右子树左边界。从而判断哪边为满二叉树。
满二叉树侧,N=2^H。非满二叉树侧,递归。
//完全二叉树节点个数
func nodeNum(root: TreeNode?) -> Int {
if root == nil {
return 0
}
return bs(node: root!, level: 1, h: mostLeftLeve(node: root, level: 1))
}
/// 以node为头的所有节点个数
///
/// - Parameters:
/// - node: 当前节点
/// - level: 当前节点层数
/// - h: 总深度
/// - Returns: 节点个数
func bs(node: TreeNode,level: Int ,h: Int) -> Int {
if level == h {
return 1
}
//比较节点右子树深度与当前树深度
if mostLeftLeve(node: node.right, level: level+1) == h {
//左树已满。2^(h-level)+右树节点数
return 1<<(h-level) + bs(node: node.right!, level: level+1, h: h)
}else {
//右树已满。2^(h-level-1)+左树节点数
return 1<<(h-level-1) + bs(node: node.left!, level: level+1, h: h)
}
}
/// 获取当前子树总高度
///
/// - Parameters:
/// - node: 头节点
/// - level: 当前层级
/// - Returns: 左边界总高度
func mostLeftLeve(node: TreeNode?,level: Int) -> Int {
var node = node
var level = level
while node != nil {
node = node!.left!
level+=1
}
return level-1
}
每层只遍历一个节点的子树,总计LogN。
每个子树获取右子树左边界遍,需要经历LogN次计算。
总复杂度O((LogN^2))
-
数组与完全二叉树
如果从下标从1开始存储,则编号为i的结点的主要关系为:
双亲:下取整 (i/2)
左孩子:2i
右孩子:2i+1
如果从下标从0开始存储,则编号为i的结点的主要关系为:
双亲:下取整 ((i-1)/2)
左孩子:2i+1
右孩子:2i+2
#这个规律,通常用来对通过指定下标取得相关节点下标。
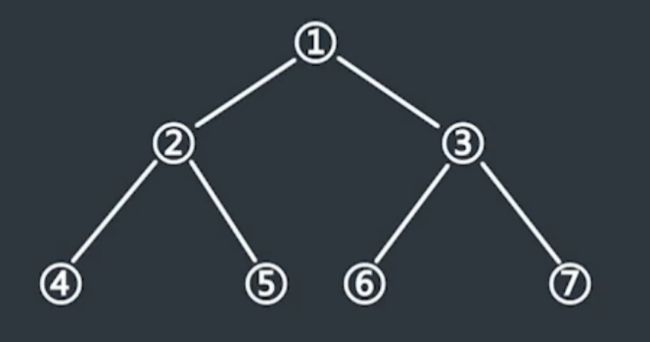
后序节点与前驱节点
中序遍历中的下一个遍历点与上一个遍历点
2的后序节点为3,2的前驱节点为1
二叉树中两节点间的距离
可以向上或向下走,但每个节点只能经过一次。
下图中2,1两节点距离为2。3,5节点距离为5
-
最大距离只有三种情况
- head左子树上的最大距离
- head右子树上的最大距离
- head左子树上离head左孩子最远的距离,加上head自身节点,再加上head右子树上离head右孩子最远的距离。也就是两个节点分别来自不同子树的情况。
三个情况下最大的结果,就是以head为头节点的整棵树上最远的距离。
参考资料
Swift 算法实战之路:二叉树
左神牛课网算法课