姓名:李嘉蔚 学号16020520034
【嵌牛导读】:梯度下降法是一个最优化算法,通常也称为最速下降法。最速下降法是求解无约束优化问题最简单和最古老的方法之一,虽然现已不具有实用性,但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的,最速下降法越接近目标值,步长越小,前进越慢。
可以用于求解非线性方程组。常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。
【嵌牛鼻子】:1. 策略参数化
2. 策略梯度算法
2.1 MC Policy Gradient
2.2 Actor-Critic
【嵌牛提问】:策略梯度是怎么用的呢?求解过程是什么?
【嵌牛正文】:1. 策略参数化
强化学习有两种场景。一种是离散的强化学习场景。在这种场景下,我们从状态抽取状态特征向量 s^ 。和价值函数近似,我们让 f(s^,a)f(s^,a) 特征向量一共有 |A| 部分,分别对应不同的动作。在 f(s^,a)f(s^,a) 特征向量, a 动作对应位置放 s^ 特征,其他动作对应位置为 0。设定参数 w。
另一种是连续的强化学习场景。在连续强化学习场景下,我们也是从状态抽取状态特征向量 s^ ,然后设定一个参数向量 w ,然后用特征和参数计算不同动作的概率。
其中动作 a 是一个实数值。策略用了标准差为 1 的高斯分布,因此该策略被称为高斯策略。容易求得高斯策略的对数梯度。
强化学习就是学习参数 w 的值。那么我们按什么样的目标学习参数 w 呢? 我们有如下三种目标。其中第一个目标适用于每次从一个开始状态出发的强化学习,另外两种目标适用于其他场景。
其中 d^(πw) 是策略 πw 稳定概率。虽然我们有三种目标函数,但是下面的策略梯度定理揭示这些目标函数的梯度是一致。只要我们求得梯度,就可以应用梯度下降相关算法了。
根据策略梯度定理,我们只要计算出 wlogπw(s^,a) 和价值 q(s^,a) ,就可以求解策略梯度优化问题了。Softmax 和高斯策略的 wlogπw(s^,a) 计算公式在上面已经介绍了。Softmax 策略的更新代码。
//policy 待更新的策略
//f 状态特征
//a 动作
//qvalue q值
//alpha 学习率
def update_softmaxpolicy(policy, f, a, qvalue, alpha):
fea = policy.get_fea_vec(f,a);
prob = policy.pi(f);
delte_logJ = fea;
for i in xrange(len(policy.actions)):
a1 = policy.actions[i];
fea1 = policy.get_fea_vec(f,a1);
delta_logJ -= fea1 * prob[i];
policy.theta -= alpha * delta_logJ * qvalue;
2. 策略梯度算法
为了求解策略梯度优化问题,我们需要计算 wlogπw(s^,a) 和价值 q(s^,a) 。按照上述内容,我们能够求得 wlogπw(s^,a) ,那怎么求解价值 q(s^,a) 呢?
2.1 MC Policy Gradient
蒙特卡罗策略梯度适用于插曲式的强化学习场景。插曲式强化学习场景中,系统会从一个固定或者随机起始状态出发,经过一定的过程之后,进入一个终止状态。比如,机器人找金币例子就是插曲式强化学习场景。蒙特卡罗策略梯度让系统探索环境,生成一个从起始状态到终止状态的状态-动作-奖励序列。
s1,a1,r1,.....,sT,aT,rT(1)
在第 t 时刻,我们让 gt=rt+γrt+1+... 等于 q(st,a) ,从而求解策略梯度优化问题。蒙特卡罗策略梯度代码如下。
def mc(grid, policy, num_iter1, alpha):
actions = grid.actions;
gamma = grid.gamma;
for i in xrange(len(policy.theta)):
policy.theta[i] = 0.1
for iter1 in xrange(num_iter1):
f_sample = []
a_sample = []
r_sample = []
f = grid.start()
t = False
count = 0
while False == t and count < 100:
a = policy.take_action(f)
t, f1, r = grid.receive(a)
f_sample.append(f)
r_sample.append(r)
a_sample.append(a)
f = f1
count += 1
g = 0.0
for i in xrange(len(f_sample)-1, -1, -1):
g *= gamma
g += r_sample[i];
for i in xrange(len(f_sample)):
update(policy, f_sample[i], a_sample[i], g, alpha)
g -= r_sample[i];
g /= gamma;
return policy
2.2 Actor-Critic
价值函数近似的强化学习算法用于估计状态-动作价值 q(s,a)。策略梯度算法引入价值函数近似提供价值是一个很好的思路。这时候,算法分为两个部分:Actor 和 Critic。Actor 更新策略, Critic 更新价值。Critic 就可以用之前介绍的 SARSA 或者 QLearning 算法。下面是 SARSA 算法代码示例。
def sarsa(grid, policy, value, num_iter1, alpha):
actions = grid.actions;
gamma = grid.gamma;
for i in xrange(len(policy.theta)):
value.theta[i] = 0.1
policy.theta[i] = 0.0;
for iter1 in xrange(num_iter1):
f = grid.start();
a = actions[int(random.random() * len(actions))]
t = False
count = 0
while False == t and count < 100:
t,f1,r = grid.receive(a)
a1 = policy.take_action(f1)
update_value(value, f, a, \
r + gamma * value.qfunc(f1, a1), alpha);
update_policy(policy, f, a, value.qfunc(f,a), alpha);
f = f1
a = a1
count += 1
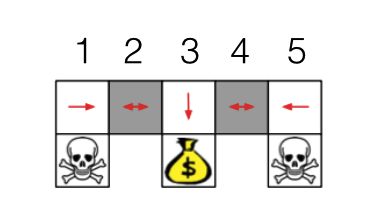
return policy;
一好处是概率化输出。在预测时,价值函数近似应用了贪婪策略或者 ϵ− 贪婪策略,选择价值最大的方向。有时候这可能会导致问题。还是拿机器人找金币做例子(如下图所示),状态特征是北(东,南,西)方向是否面对墙。状态 2 和 状态 4 的状态特征一样,贪婪策略或者 ϵ− 贪婪策略采取相同动作。如果动作是向右,则状态 4 之后会陷入 4 和 5 之间的循环。如果动作是向左,则状态 2 之后会陷入 1 和 2 之间的循环。但是如果我们采用策略梯度,在状态 2 和状态 4,学习到的策略输出向右和向左动作的概率都是 0.5,从而不会陷入循环。