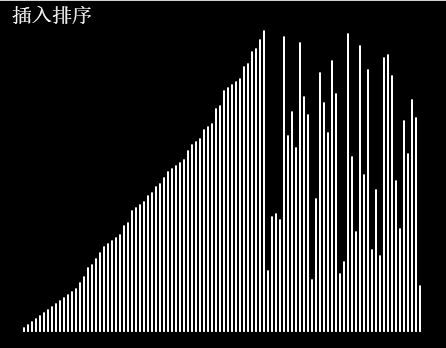
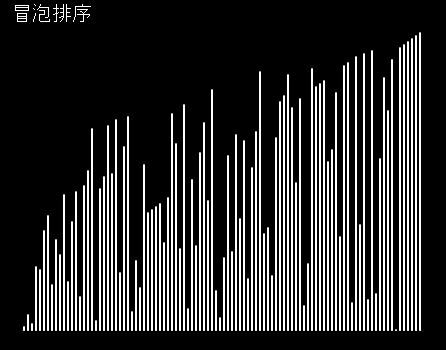
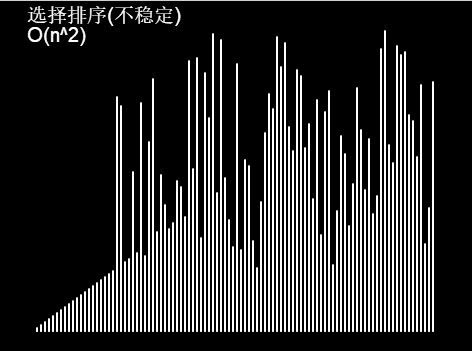
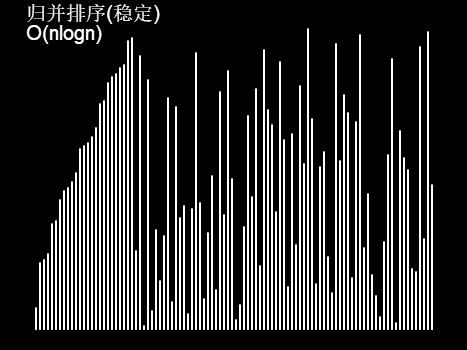
插入排序:
时间复杂度O(n^2)
代码很短,解释一下,l是要排序的部分的最左一位,r是最右一位,为了方便理解,这里l=1,r=10。
插入排序的主要思想是每次往已经有序的序列中插入一个数,这里可以把i左边的看成已经有序的,i右边的看为正在排序的序列,第i位即是当前所需插入的数。
我们逐句分析:i设定为1+1,也就是第二位,重复执行直到i>10。
这里可以看成for(int i=1+1;i<=10;i++)也就是从第2位扫到第10位。
然后j设定为1,重复执行知道j>i-1也就是从第1位扫到第i-1位,直到找到一个比当前需要插入的数还要大的数,将数插入。
假设有一个序列{1,3,5,2,8,4,9,6,10,7}
我们来模拟一下原程序。
{1,3,5,2,8,4,9,6,10,7}
——i—————————————-
{1,3,5,2,8,4,9,6,10,7}
———–i———————————–
{1,3,5,2,8,4,9,6,10,7}
—————-i——————————
{1,2,3,5,8,4,9,6,10,7}
——————–i————————–
{1,2,3,5,8,4,9,6,10,7}
————————-i———————
{1,2,3,4,5,8,9,6,10,7}
——————————i—————-
{1,2,3,4,5,8,9,6,10,7}
———————————-i————
{1,2,3,4,5,6,8,9,10,7}
—————————————-i——
{1,2,3,4,5,6,8,9,10,7}
———————————————i-
{1,2,3,4,5,6,7,8,9,10}
———————————————–i 这时i>10跳出循环。
插入排序是一种很容易理解的排序,但是速度较慢。
冒泡排序:
时间复杂度O(n^2)
代码也很短。
冒泡排序的思想是重复走这个序列,每次比较两个相邻的元素,如果发现他们不符合顺序便交换两者。这个很好理解。就不过多解释了,另外提一下,如果比较的时候用的是>或<小于,冒泡就是稳定的,但如果用的是≥或≤,冒泡便变成了不稳定的算法。
选择排序:
顾名思义,每次找到未排序部分最小的数,放到已排序序列的末尾。
本来有个模拟的。。。不小心刷新网页了
不想再写一遍
其实很好理解的啦,仔细看看
归并排序(开始比较精彩的了):
程序:
归并排序是一个采用分治法的一个非常经典的运用,没错,用到了递归
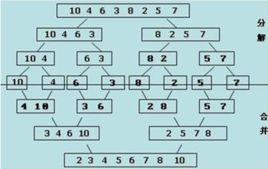
我们来看一张图:
这个程序先将这个序列拆分成很多个小序列(程序上面一部分),拆分到无法拆分时便开始合并。
合并过程很简单(程序下面一部分),其实就是二路归并,这里贴个链接,讲的很详细:https://www.cnblogs.com/chengxiao/p/6194356.html)
因为每一边的序列都是有序的,所以可以用这种二路归并的方式。
归并排序的缺点就是空间占用大,我们需要另一个数组来储存归并后的序列,然后再复制到原数组。
快速排序(喜闻乐见):
气死我了,写了一大堆全没了
https://www.cnblogs.com/MOBIN/p/4681369.html这个链接讲的挺好的,对应着看看吧
堆排序:
堆排序对于新手来说可能会很懵逼(我不就是新手吗),所以程序放后面。
堆排序需要涉及到很多个概念。(都知道可以跳过)
接下来的资料来源于百度百科,一些教程与理解是我自己写的。
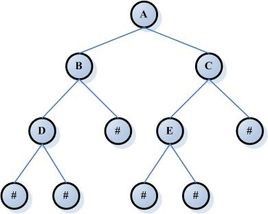
树:
树状图是一种数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个结点有零个或多个子结点;没有父结点的结点称为根结点;每一个非根结点有且只有一个父结点;除了根结点外,每个子结点可以分为多个不相交的子树。
(这就是一颗典型的树)
二叉树:
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。(摘自百度百科)(比如上面那个树就是个二叉树)
完全二叉树:如果一棵具有n个结点的深度为k的二叉树,它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应,这棵二叉树称为完全二叉树。
完全二叉树有一个很方便的性质,假设有一个完全根结点编号为1的二叉树,有一个结点的编号为i,那么它的左儿子为2*i,右儿子为2*i+1,而它的父亲即为i/2(因为在c++中,当“/”用于两整型操作数相除时,其结果取商的整数部分,小数部分被自动舍弃,也就是向下取整(i/2))
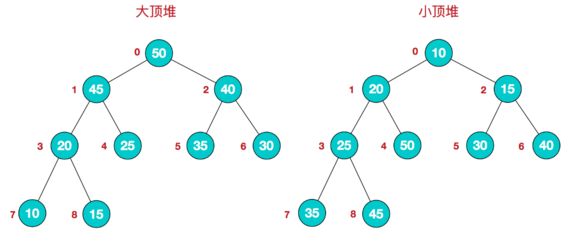
堆:
堆(英语:heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的定义如下:n个元素的序列{k[1],k[2],k[i],…,k[n]}当且仅当满足下关系时,称之为堆。
(k[i] <= k[2*i],ki <= k[2*i+1])或者(k[i] >= k[2*i],k[i] >= k[2*i+1]), (i = 1,2,3,4…n/2)
上面讲过了,2*i是这个结点的左儿子,2*i+1是这个结点的右儿子。
若将和此次序列对应的一维数组(即以一维数组作此序列的存储结构)看成是一个完全二叉树,则堆的含义表明,完全二叉树中所有非叶结点的值均不大于(或不小于)其左、右孩子结点的值。由此,若序列{k[1],k[2],…,k[n]}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
如果你理解了完全二叉树,堆将会很好理解:
(配合图片食用更佳)
那么接下来终于到正题了。
堆排序:
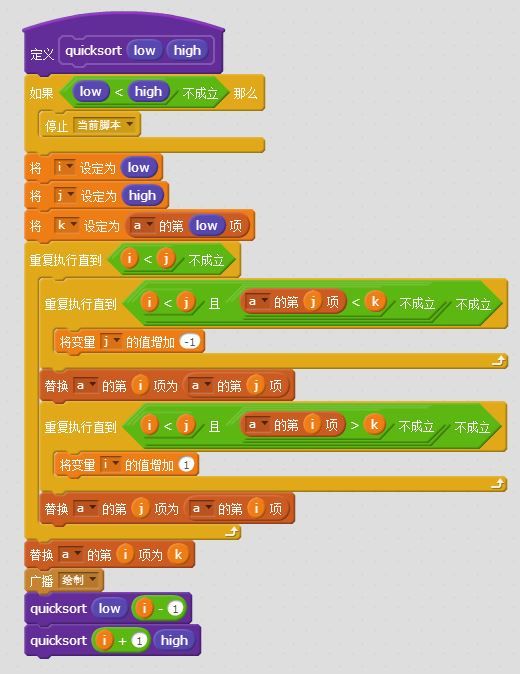
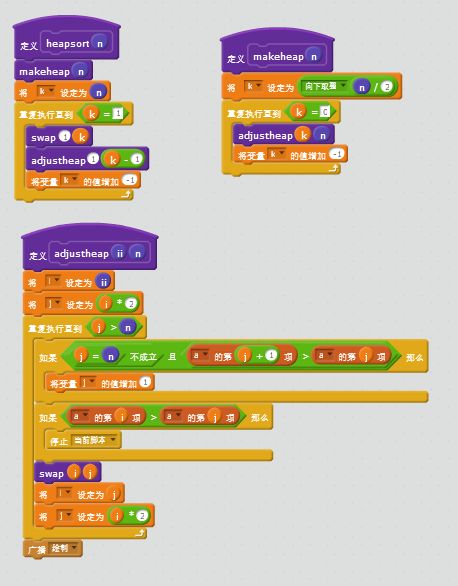
可以看到,我们先建立了一个大根堆,向下取整(n/2)代表的是最后一个父结点(也就是最后一个有儿子的节点),然后枚举之前的所有点,因为完全二叉树的性质,之前的所有点一定都是有儿子的。然后将这些点调整(下面那个自定义程序),我们来理解一下,i表示当前要调整哪个点,j表示要调整的点i中较大的儿子(后面那个判断即是为了找出较大的儿子)。
如果发现i这个节点不符合当前构造的堆的规律(它较大的那个儿子比自身大),那么便交换这个结点与它的儿子结点j。由于交换后可能导致以下的部分混乱,于是我们将i设定为j,继续交换,直到符合堆的规律或者j比n大了。
那么这样一个堆就建好了,那排序怎么做呢?还记得吗一个大根堆(或小根堆)的根一定是整个序列中最大(或最小)的,堆排序便是利用了这个特点。
一个堆的根结点必定是整个序列最大的。于是我们交换根结点和最后一个结点,将最后一个结点排除在堆外,然后重建这个堆(这时候堆的大小-1)重复这个过程直到堆中没有结点了。这时候我们的排序就排好了。
总结一下:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。