一、神经网络(Neural NetWorks)的基本结构
神经网络是由神经层(layer)搭建起来的。由输入层,隐藏层、输出层组成。输入层就是特征的输入;隐藏层有多层,包含神经网络自生成的新特征(输入特征的多次项组合);输出层为预测结果。简单的神经网络如下图所示:
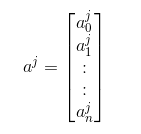
其中$a_{i}^{j}$表示第j层第i个节点,每一条带箭头的线,都有不同的权重参数,相当于之前讲过的模型参数θ,表示符号为$\Theta_{ik}^{j}$,含义为:第j层第k个节点指向(j+1)层第i个节点的权重。在计算第(j+1)层节点时,往往加入$a_{0}^{j}$,作为偏置,其值为1。基于神经网络可以写出各节点、输出与输入的关系式:
$a_{i}^{j}=function(\sum_{k=0}^{n} \Theta _{ik}^{j-1}a_{k}^{j-1}) $
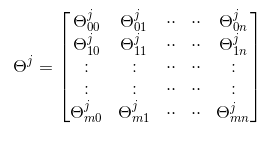
其中function可以是逻辑回归中的逻辑函数,也可以像线性回归直接将求和结果作为输出。下面给出节点的列向量形式和权重的二维矩阵形式:
根据这两个列向量,我们可以将关系式以矩阵形式给出:
$a^{j}=\Theta^{j-1}a^{j-1}$
对于上面图中例子,可以用矩阵表示输入与输出的关系,为了跟图中统一,输入层视作第一层,输出层为第3层:
$a^{2}=\Theta^{1}x$
$a^{3}=\Theta^{2}a^{2}$
$h_{\Theta}(x)=a^{3}$
二、神经网络的二分类实例
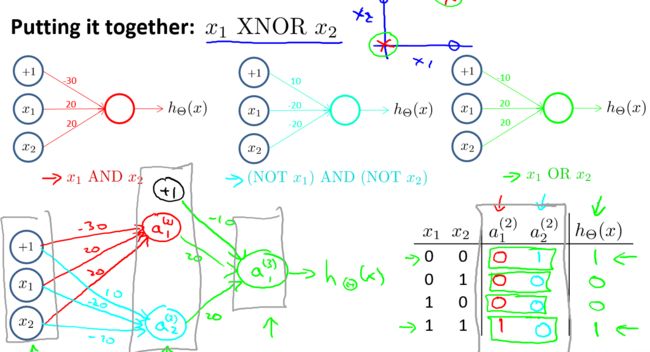
神经网络之所以能很好地解决非线性回归,在于它可以创造并选择最好的多项式。对于网络第一层(输入层),每个节点都是一次项,第二层是二次项,第n层是n次项。也就是说正常情况下神经网络层数越多,功能也就越强大。神经网络自动调节权值,来强化某个多项式的作用,或弱化某个多项式的影响。来看一个神经网络实现逻辑回归的例子:
对于与运算,当输入全为1是,结果为10,根据逻辑函数,其概率应该接近于1;当输入不全为1时,结果小于-10,其概率接近于0。或非、或运算也是这个道理。在实际应用中,我们只要给出一堆训练数据,神经网络就可以学会这些权值,而不用人工调节。再来看同或运算,输出与输出层不变,隐藏层可以看做神经网络自己添加了一个新节点(实际上是强化),这样通过两个隐藏节点就可以实现比与或非复杂的运算,而这一切都是神经网络自己学习所得。
三、神经网络的多分类
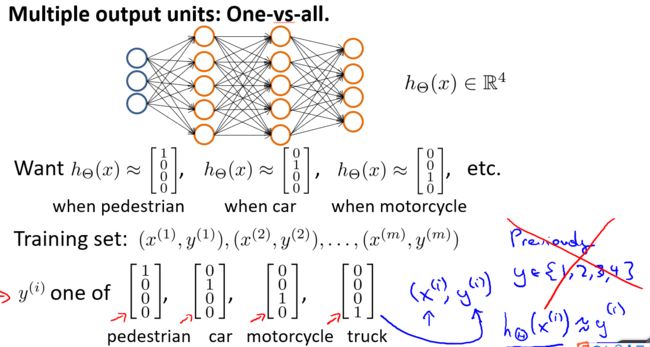
在《机器学习笔记(二)》中曾讨论过多元逻辑回归,当时的思想是维护多个假设函数,然后最终比较各个函数算出来的概率大小。在神经网络中,我们重新定义解决多分类的方法。
如上图,表示了四分类的网络结构,输出层共四个节点,分别代表各分类的结果(0/1),实际上这张网络也是维护了4个假设函数。不同于之前的定义,这里将结果用列向量来表示。网络的目标是使输出层尽可能符合所给的列向量$y^{i}$。