从2017年5月7日开始,我开始阅读一本从罗胖子那边买来的书《囚徒困境——冯诺依曼、博弈论和原子弹之谜》如果说,活了25年,让我排一下至今对我影响最大的前几本书
这本书,我可以排到前三位
至于为什么,就是我今晚码字的原因
容我细细道来
关于占了整本书三分之二篇幅的有关冯诺依曼、原子弹和博弈论的历史,我毫无兴趣,就此略过
我会分四个大部分,简要介绍在我眼中,这本书带给我如醍醐灌顶般的启发
“囚徒的困境”的描述
关于这个经典的博弈情景,包括我在内的很多人都听过,大学里的公共课程也都做过类似的介绍或者是实验
我这里与诸君一同回忆一下
这个博弈第一次被在公共场合提出来,是1950年普林斯顿大学的数学家塔克在斯坦福大学为心理学系做的讲座:
“
两个被指共同犯法的人被警察分别关押。两人都被告之:
1、如果一个人招供而另一个人不招供,前者将获得奖励,后者将受到惩罚
2、如果两个人都招供,那两个都要受到惩罚,但程度要比1的程度轻
3、如果两个人都不招供,两个人都会无罪释放
”
作为一个理科生,阅读文字永远都不如图表和量化来的清晰:
虽然量化了,但是似乎奖励越好对应的数字越小,不直观!
所以将以上图表再做优化,从“判刑”模式变成“得分”模式
即:1、甲乙都合作,各得2分;
2、甲乙都背叛,各得1分;
3、甲背叛,乙合作,甲得3分,乙得0分
4、甲合作,乙背叛,甲得0分,乙得3分;
这里把0分称为“傻瓜回报”,1分称为“惩罚回报”,2分称为“奖励回报”,3分称为“引诱性回报”
“囚徒的困境”的“理性”结果
书中有提到过“纳什均衡”这个概念,不过书中并没有将从数学角度去证明,而是用了一个通俗的解释,对于这种形式我很喜欢。
简而言之,数学家约翰纳什对博弈的分析方法是类似于“马后炮”式的事后分析:
“
在博弈之后,对每个参与者进行事后分析
轮流询问每个参与者
在对手玩法确定的前提下
你是否要对自己的抉择进行改动
直到每个人都乐于接受自己的结果
则该结果就是平衡点
”
用此方式对上述囚徒困境进行分析:
1、对甲而言,如果乙选择合作(乙C):自己选择合作(甲C),得2分;自己选择背叛(甲B),得3分。所以对于甲,在乙选择合作的情况下,甲不后悔的均衡点是“背叛”(B)
2、对甲而言,如果乙选择背叛(乙B):自己选择合作(甲C),得0分;自己选择背叛(甲B),得1分。所以对于甲,在乙选择背叛的情况下,甲不后悔的均衡点是“背叛”(B)
对于乙来说,结果也是一样。
通过事后的“马后炮”分析,甲、乙双方都不后悔的“均衡点”都是背叛(Betray)
但是回过头来想一想,似乎哪里不对
为什么双方都不后悔的决定,最后的结果是“两败俱伤”?
明明从上帝视角来看,双方都合作才是最好的结果
这里“集体利益”与“个人利益”产生了明显的冲突
“理性”的人会陷入困境——囚徒的困境
那到底是因为什么,才会导致这种囚徒困境呢?
即,当“傻瓜回报”(0分)<“惩罚回报”(1分)<“奖励回报”(2分)<“引诱回报”(3分) 时就会出现囚徒困境
所以,如果一种博弈或者说一种选择
“互相合作(CC)”的共同利益还比“祈祷对方是个傻子”(BC或CB)时要低
这种情况下就会出现囚徒困境
(生活中,人都希望别人都是傻子,只有自己是聪明人)
这种情况下的唯一的“理性”结果,就是双方都受到惩罚(BB)
两败俱伤!
单次的囚徒困境有解吗?
目前没有,看上去永远也不会有
解决囚徒困境的唯一方法,就是避免囚徒困境
所以一个好的社会、好的公司、好的团体,就是要标榜道德、公司文化和价值观去促进合作(CC)
另一方面去立法、立规去惩罚背叛(BC、CB、BB)
否则,由理性带来的BB会对集体利益造成伤害
关于多次的囚徒困境
第二部分讲的理性结果是基于囚徒困境只进行一次的情况下
书中还提到了多次囚徒困境
即,由多人、多次进行囚徒困境的博弈
如何在个人利益和集体利益之间获得平衡?
当然,从上帝视角来看
“
CC的集体得分是(2+2=4分)
BC和CB的集体得分是(3+0=3分)
BB的集体得分是(1+1=2分)
”
无疑,如果双方一直合作CC下去,集体得分最高,个人得分也相对可以接受
但是第二部分双方均不后悔的“理性”结果告诉我们
只进行一次的囚徒困境博弈,互相背叛BB似乎是唯一解
但在多次博弈的背景下,采用什么策略才更加“理性”?
这里,书中提到了一种实验方法
先建立不同种的策略,每种策略用一段脚本表示
然后让所有的策略两两博弈,经过足够多的博弈后,看每种策略的得分:
这里选取了几个比较有特点的策略:
1、永远合作的好人派(ALL C)
2、永远背叛的理性派(ALL B)
3、神经兮兮的随机派 (Random)
4、一报还一报(TT)
注释:
一报还一报是指,如果对方本回合背叛,则自己则会在下一回合报复;如果对方本回合合作,则自己会在下一回合合作。
TT:书中把一报还一报称为“TIT FOR TAT”,我也不知道啥意思
囚徒困境的分值设置和上面一样:
1、甲乙都合作(CC),各得2分;
2、甲乙都背叛(BB),各得1分;
3、甲背叛,乙合作(BC),甲得3分,乙得0分
4、甲合作,乙背叛(CB),甲得0分,乙得3分;
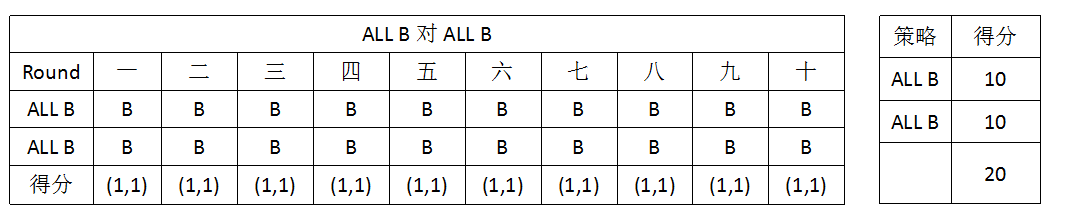
然后让两两进行博弈测试,类似于下图:
因为书中提到的策略有很多种,有一些是基于上述几个策略的改良:
1、一报还两报:对方背叛一次,下两回合都会背叛,之后才恢复合作
2、两报还一报:对方连续背叛两次,下一回合才背叛,否则一直合作
3、90%一报还一报:对方背叛一次,下一回合90%几率会背叛,之后才恢复合作
.............
据说最长的一个策略,用代码语言表示,写了几百行
有兴趣的人,可以用python或JS把上面的策略都列出来,大家都捉对厮杀,看最后得分
书中直接给出了结论:
“一报还一报”策略在多人多次的囚徒困境中胜出,是最优策略
虽然ALL B的策略符合单次囚徒困境的理性结果,但是在多种策略的竞争下
因为背叛带来的系统性分值降低而在整体得分上输给了“一报还一报”
因为在很多回合的博弈中,ALL B策略一直在逼迫合作者背叛,最后的结果往往是怀揣善意想合作的人被迫背叛而两败俱伤
而ALL C策略则相反,一直在引诱对方背叛,最后往往被ALL B这种凶狠的策略所剥削,得分比ALL B还要惨
而一报还一报TT策略则相对有原则
“一报还一报”从不“剥削”任何策略,也不向任何凶恶的策略低头
这个策略没能打败任何人,但是它最终赢得了比赛
书中还提到了一个很“有趣”的现象——一报还一报策略之间博弈的回声现象
如表展示,如果两个TT策略中某一个进行中途叛变,之后双方仍然坚守自己“一报还一报”的策略,就会陷入一个互相背叛的过程,永不停止。
而互相背叛的平均得分则低于双方共赢时的平均得分。
这个回声现象给我的启示:两个互相信任且要强人,如果一方在合作中途丢了初心(选择背叛),那么双方将陷入无止尽的相互背叛当中,再难以回到双赢的局面
囚徒困境给我的震撼与启示
1、一切都是囚徒困境
第一次听到一个博弈的时候,我觉得就是一帮闲的蛋疼的逻辑怪想了个题来消遣,心里不断repeat一句话
“研究这个有什么用?能改善生活吗?”
后来这本书里的一句话让我醍醐灌顶
“只要有利益冲突的地方,就会有囚徒的困境”
而在利益纠缠的生活中
工作上一起合作做一件事,外卖来了谁去拿一下外卖,吃完饭了谁来买一下单
甚至恋爱阶段男女双方的相处
经常在新闻上看到两国关系的新闻,美国对俄罗斯在AAA方面进行制裁,第二天,俄罗斯对美国在BBB方面进行制裁。那时候觉得好幼稚,好无聊。现在想一想,这不就是“一报还一报”吗?
“一切都是囚徒困境”
而如果基于所谓
理性、不后悔的博弈选择
所有的结果都会是
背叛背叛背叛
也许并不是因为人品很差劲,而是陷入了这种困境
如果将“奖励性回报”提高,同时降低“引诱性回报”,将双方从困境中解救出来
(公司完善绩效考核机制、惩罚不作为的员工、拿外卖的人少付一份钱,不拿的人多付一份钱、吃完饭第一个买单的朋友可以和餐厅里漂亮小姐姐跳一支舞)
或许这样,合作、忠诚、友情、爱都将回归
2、我应当做一个什么样人?我应当如何教育我的子女?
一切都是囚徒困境
那么人与人之间的关系就是
一次性囚徒困境博弈与重复性囚徒困境博弈组合
每个人都有一个自己的策略,与社会上形形色色的人进行博弈
每个人在每次博弈之后的总分,就是代表自己的生活质量与地位
遇到不顺心的背叛者(ALL B)或者其他侵略性较强的人
我们可能会选择“背叛”来保证自己的单次利益
或者在社会的逼迫或者所谓良心的谴责下选择“合作”而得到“傻子回报(0分)”
为了得到更多的分数,以后只会与这种人进行少量甚至只有一次的接触(单次囚徒困境博弈)
如果与一个一生只会见一面,做一次囚徒困境博弈的人进行博弈,最好还是选择背叛
但是很多情况下,我们被迫与一些人不得不进行多次博弈:
同一部门的员工,自己的亲人,自己的同学朋友
有些亲密关系(父母、兄弟)带来强烈的信任感,我们可以选择永远合作(ALL C)来保证得分最大化
有些缺乏信任感但又不得不进行多次博弈,那我们该怎么办?
“一报还一报”的策略是所有重复囚徒困境博弈的最优解
所以,我应该做一个“一报还一报”的人,用人的语言来讲:
我应当以合作为先,去拥抱世界,但是要爱憎分明,睚眦必报!
爱憎分明是为了让自己的行为具有“可预测性”,让ALL C的人放心大胆合作,也让心里有着“背叛”念想的人知道背叛的后果将是下一回合毫无余地的报复
睚眦必报并不是没有胸怀,胸怀是在你背叛后再次来合作,我仍然以合作的态度与你进行更下一个回合的博弈。
不翻旧账,但是旧账必须要算完
我爸爸妈妈从小都是老实人,爷爷奶奶外公外婆都是辛勤劳作的农民
中华民族优良的传统品质流淌在他们的血液里
他们教育我,要相信他人的好,原谅他人的错,得饶人处且饶人
其实就是告诉我,要做一个(ALL C)策略的人
但是在这个处处都是囚徒困境博弈的社会上
ALL C的唯一结局只能是被凶狠的背叛为主的策略们无情剥削、欺骗
以前,我一直都很迷茫,到底是听妈妈的话,做一个温和、善良的老实人
还是彻底堕入囚徒的“理性”圈套,做一个ALL B?
这里我终于找到了支持“一报还一报(TT)”世界观为最优解的理论数学基础!
以后我也会教育我的子女,一定要做一个一报还一报(TT)的人
不因为别的,而是让信任你的人更信任,让背叛你的人不好过,让有背叛之心的人知道下场!
3、我应当多和什么样的人在一起?
试想一下这个重复囚徒困境实验:
“
在一个“ALL C”的策略池中,放入几个“ALL B”,然后每轮博弈的后得分最低的几位被淘汰,很显然,ALL C 的策略们在与自己交手时会得到奖励回报(2分),而在与ALL B策略交手时会得到傻瓜回报(0分),对方得到引诱回报(3分)。如果所有的策略可以像细菌一样进行自我繁殖,这个ALL C的群落就会慢慢被ALL B策略所取代。但是整个群落最后会从互相合作的高得分群落(2+2)变成一个互相背叛的低得分群落(1+1),灭绝的原因就是引来了几个凶狠ALL B。
”
任何高尚群体都要远离以背叛、剥削为主的个体,因为一两个就会彻底腐化整个系统
另一个实验:
“
在一个“ALL B”的策略池中,放入几个“ALL C”,不用过多分析,在规定必须与所有群落成员进行博弈得分的条件下,几个ALL C分分钟被淘汰
”
ALL C进入到不明的凶狠群体,如果不能学会抱团取暖,就永远是别人眼中的肉
第三个实验:
“
在一个“ALL B”的策略池中,放入几个“TT(一报还一报)”,TT与ALL B博弈时,TT在第一轮遭受背叛后的行为与ALL B保持一致;TT与TT自己博弈时,行为则与ALL C保持一致;所以每轮,ALL B成员每次博弈的平均得分为1分,而TT成员每次博弈的平均得分将高于1分;最终,TT将在ALL B的群落中胜出!
”
即使在恶劣、充满背叛的ALL B环境中,一报还一报者(TT)在面对ALL B时保持凶狠,在面对自己人时抱团取暖。即使一开始人数占比在整个群落中很低,但是只要保持初心,守住原则,最终还是会胜出。
这里TT与ALL B对阵时,行为与ALL B无异。这个现象让我想到一个现象,很多人的策略一开始是好的,但是在恶劣的环境中为了保护自己,只能也变得凶狠,有些人直接就忘记了自己是TT,彻底沦落成了ALL B那种Loser,最终只能被淘汰。
所以,我应当多和什么人在一起?
在无情的社会中,有太多凶狠的掠夺者,他们有时候一下子攫取了很多利益(3分),但是他们不是这个自然界最终的胜者。作为一个一报还一报TT者,只要守住初心和原则,不和ALL B们同流合污。找到自己的战友们TT,未来始终是我们的。
4、其他的一些碎碎念与呢喃
社会的问题很复杂,很多事情不是简单的囚徒困境就能解释的,毕竟囚徒困境只有合作和背叛两种选择,但是我相信爱憎分明、守住初心的世界观是正确的,世界不会是ALL B的世界,将会是TT的美好明天。
上文提到过,恋爱中男女的关系似乎也是某种囚徒困境
是,也不是
TT的策略在这里似乎很不适用了
因为一报还一报策略中,突发状况造成的回声效应(上文有提过)会让双方进行轮流的背叛与合作
而降低最终的整体得分
也许在之后的某一次博弈中
一方认为ta处在多次重复性博弈中
而另一方则认为这一次其实是最后一次博弈了
书中有一句话
如果你所爱的那个人不愿意做出牺牲,那么你最好成全她,记住,你是真心爱着那个人的。
是的吧
给对方引诱性回报的3分
总比为了惩罚性回报的1分而最终闹的不可开交要好吧
I love you,so I choose ALL C for you,though you still leave me in the end.