FFT及其框图实现
\(FFT\)的全称为快速傅里叶变换,但是\(FFT\)并不是一种变换,而是实现\(DFT\)的一种快速算法。当\(N\)比较大时,使用\(FFT\)可大大减少进行\(DFT\)变换的计算量。
\(N\)点的\(DFT\)所需的计算量为:
\[ X[k]=\sum_{n=0}^{N-1}x[n]W_N^{kn} \]
乘法:\(N^2\)次,加法:\(N(N-1)\)次。每当\(N\)提高一倍,计算量增大四倍。
基\(2\)时域抽取
假设有一长度为\(2N\)的有限长序列\(x[n]\),现对其进行\(DFT\)变换,现有一算法可以将\(2N\)点的\(DFT\)计算降为\(N\)的\(DFT\)计算,记\(g[n]\)为\(x[n]\)的下标为偶数时的序列,即\(g[n]=x[2n],0\leq n \leq N-1\),记\(v[n]\)为\(x[n]\)的下标为奇数时的序列,即\(v[n]=x[2n+1],0\leq n \leq N-1\),则
\[ \begin{aligned} X[k]&=\sum_{n=0}^{2N-1}x[n]W_{2N}^{kn}\\ &=\sum_{n=0}^{N-1}x[2n]W_{2N}^{k2n}+\sum_{n=0}^{N-1}x[2n+1]W_{2N}^{k(2n+1)} \\ &=\sum_{n=0}^{N-1}g[n]W_N^{kn}+W_{2N}^k\sum_{n=0}^{N-1}v[n]W_N^{kn} \\ &=G[
当\(0 \leq k \leq N-1\)时
\[ X[k]=G[k]+W_{2N}^kV[k] \]
当\(N \leq k \leq 2N-1\)时
\[ X[k]=G[
其中\(g[n]\)和\(v[n]\)的\(DFT\)都是\(N\)点的。
两个\(N\)点的\(DFT\)的运算量(以乘法为例)为\(2N^2\),而一个\(2N\)点的\(DFT\)运算量为\(4N^2\),计算量减少了一半!如果\(N=2^r\),则可以一直降下去,从而大大的减少了计算量。通过计算,可以知道此时的计算量为:乘法:\(\dfrac{N}{2}log_2N\),加法:\(Nlog_2N\)。
下面以8点的\(DFT\)为例,其实现框图为:
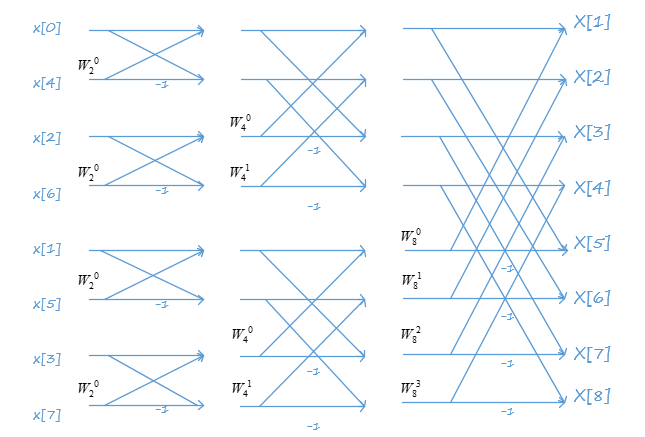
基\(2\)频域抽取
依然对于\(2N\)点的序列\(x[n]\)进行\(DFT\)计算,这次将\(x[n]\)分为前后两部分,即\(g[n]\)为\(x[n]\)的前\(N\)个点,即\(g[n]=x[n],0 \leq n \leq N-1\),\(v[n]\)为\(x[n]\)的后\(N\)个点,即\(v[n]=x[n+N],0\leq n\leq N-1\),则:
\[ \begin{aligned} X[k]&=\sum_{n=0}^{2N-1}x[n]W_{2N}^{kn}\\ &=\sum_{n=0}^{N-1}x[n]W_{2N}^{kn}+\sum_{n=N}^{2N-1}x[n]W_{2N}^{kn} \\ &=\sum_{n=0}^{N-1}x[n]W_{2N}^{kn}+\sum_{m=0}^{N-1}x[m+N]W_{2N}^{k(m+N)}\\ &=\sum_{n=0}^{N-1}g[n]W_{2N}^{kn}+(-1)^k\sum_{n=0}^{N-1}v[n]W_{2N}^{kn} \end{aligned} \]
对其进行频域抽取
\[ X[2r]=\sum_{n=0}^{N-1}g[n]W_{2N}^{2rn}+\sum_{n=0}^{N-1}v[n]W_{2N}^{2rn}=G[k]+V[k],0\leq r \leq N-1 \]
\[ X[2r+1]=\sum_{n=0}^{N-1}g[n]W_{2N}^{(2r+1)n}-\sum_{n=0}^{N-1}v[n]W_{2N}^{(2r+1)n}=W_{2N}^{n}(G[k]-V[k]) \]
该算法也将\(2N\)点的\(DFT\)降为了2个\(N\)点的\(DFT\)。
将上面时域抽取的实现框图中所有的\(x[n]\)换成\(X[k]\),然后所有箭头反向,即输入变输出,输出变输入,得到的框图就是频域抽取实现的框图。