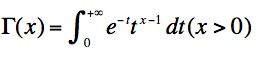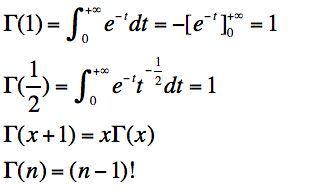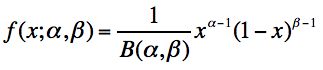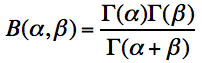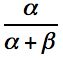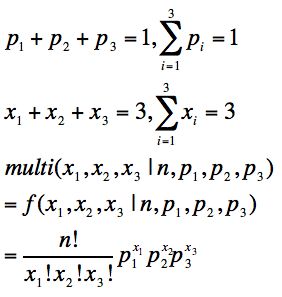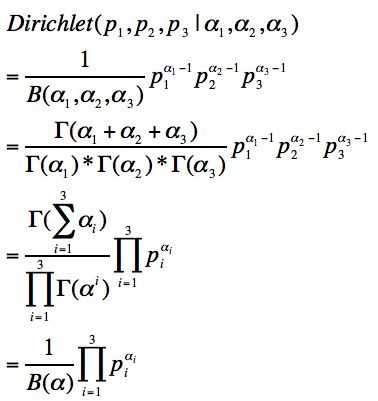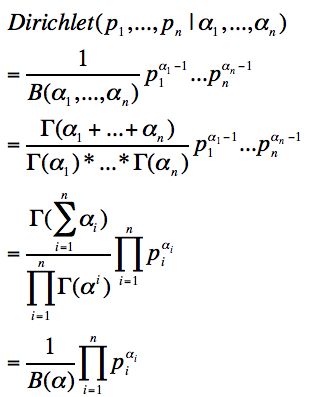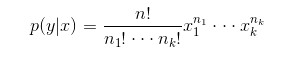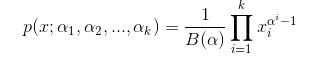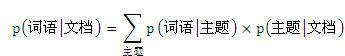概率论中两大学派:
频率学派和贝叶斯学派。先验概率,后验概率,共轭分布和共轭先验是贝叶斯学派中的几个概念。原因是贝叶斯学派认为分布存在先验分布和后验分布的不同,而频率学派则认为一个事件的概率只有一个。
基本概率分布:
先验分布(prior probability),后验分布(posterior probability),似然函数(likelyhood function),共轭分布(conjugacy)
共轭分布(conjugacy):后验概率分布函数与先验概率分布函数具有相同形式
那么对于抛硬币这个事件来说,抛出正面硬币的概率就应该是一个概率的概率,也就是说它的结果不是一个单一的值 1/2,而是一个概率分布,可能有很高的概率是1/2,但是也有一定的概率是100%(比如抛100次结果还真都100次都是正面)。那么在这里这个概率的分布用函数来表示就是一个似然函数,所以似然函数也被称为“分布的分布”。用公式来表示就是:后验概率∝ 似然函数*先验概率
采用共轭先验的原因:
可以使得先验分布和后验分布的形式相同,这样一方面合符人的直观(它们应该是相同形式的)另外一方面是可以形成一个先验链,即现在的后验分布可以作为下一次计算的先验分布,如果形式相同,就可以形成一个链条。
为了使得先验分布和后验分布的形式相同,我们定义:
如果先验分布和似然函数可以使得先验分布和后验分布(posterior distributions)有相同的形式,那么就称先验分布与似然函数是共轭的。所以,共轭是指的先验分布(prior probability distribution)和似然函数(likelihood function)。如果某个随机变量Θ的后验概率 p(θ|x)和气先验概率p(θ)属于同一个分布簇的,那么称p(θ|x)和p(θ)为共轭分布,同时,也称p(θ)为似然函数p(x|θ)的共轭先验。
参数估计:
离散型随机变量分布:二项式分布,多项式分布;
连续型随机变量分布:正态分布。
他们都可以看作是参数分布,因为他们的函数形式都被一小部分的参数控制,比如正态分布的均值和方差,二项式分布事件发生的概率等。因此,给定一堆观测数据集(假定数据满足独立同分布),我们需要有一个解决方案来确定这些参数值的大小,以便能够利用分布模型来做密度估计。这就是参数估计。
从两个学派角度考虑参数估计:
频率学派:通过某些优化准则(比如似然函数)来选择特定参数值;
贝叶斯学派:假定参数服从一个先验分布,通过观测到的数据,使用贝叶斯理论计算对应的后验分布。
先验和后验的选择满足共轭,这些分布都是指数簇分布的例子。
它们之间的关系可以通过贝叶斯公式进行连接: 后验分布 = 似然函数* 先验分布/ P(X)
Gamma函数
gamma函数其实就是阶乘的函数,比如n!=1*2*3*….n,这个阶乘形式可以更一般化,不局限于整数。而更一般的函数形式就是gamma函数:
二项分布与beta分布
二项分布(Binomial distribution)其中p为成功的概率,记作X~B(n,p)
beta分布(beta distribution),一组定义在区间(0,1)的连续概率分布,有两个参数α和β,且α,β>0.它是一个作为伯努利分布与二项分布的共轭先验分布的密度函数。Beta分布的概率密度函数:
记作X~ Beta(α,β),其中分母函数为B函数,B函数是一个标准化函数,它只是为了使得这个分布的概率密度积分等于1。
B函数与Gamma函数的关系:
Beta分布的期望可以用公式来估计:
二项分布代入似然函数:
beta分布代入先验分布:
最后我们发现这个贝叶斯估计服从Beta(a’,b’)分布的,我们只要用B函数将它标准化就得到我们的后验概率:
多项式分布与Dirichlet 分布
狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布,也就是它与多项分布具有相同形式的分布函数。
多项分布是二项分布的推广,在n次独立试验中每次只输出k种结果中的一个,且每种结果都有一个确定的概率p。
三项多项式表达:
三维Dirichlet分布:
多项式表达式:
多维的Dirichlet分布:
多项式分布代入似然函数
Dirichlet分布代入先验分布
后验概率:
LDA
主题模型的概率表示:
p(词语|文档)可通过观察数据集求得。那么右边的两个概率分布如何求得的?将这两个分布看着是上帝的游戏:上帝为了创造一篇文档,先用一个有M个面的骰子做实验,M个面代表M个主题,每做一次投骰子实验,就可以得到M个主题中的一个,进行多次投掷,就可以得到一篇文档的多个主题,可以看到这个实验描述的分布就是多项式分布。同样的某个主题下有多个词语,某个主题骰子有N个面,每个面表示一个词语(即词袋),每做一次投骰子实验,就可得到N个词中的一个,进行多次投掷,就可以得到一个主题下多个词语,同样可以看出这个实验也服从多项式分布。我们可以将他们的先验都取Dirichlet分布。
http://wulc.me/2017/01/08/%E5%85%88%E9%AA%8C%E6%A6%82%E7%8E%87%EF%BC%8C%E5%90%8E%E9%AA%8C%E6%A6%82%E7%8E%87%EF%BC%8C%E5%85%B1%E8%BD%AD%E5%88%86%E5%B8%83%E4%B8%8E%E5%85%B1%E8%BD%AD%E5%85%88%E9%AA%8C/
http://blog.csdn.net/claire7/article/details/46780849
http://blog.csdn.net/michael_r_chang/article/details/39188321
http://www.cnblogs.com/yutingliuyl/p/7064997.html
http://blog.csdn.net/omade/article/details/17023091
http://blog.csdn.net/a358463121/article/details/52562940
http://blog.csdn.net/a101070096/article/details/50459137
http://blog.csdn.net/xianlingmao/article/details/7340099
http://blog.csdn.net/u010945683/article/details/49149815
http://blog.csdn.net/michael_r_chang/article/details/39188321
http://blog.csdn.net/acdreamers/article/details/45026459